Energieumwandlung der Sterne
![]() Nichts geht ohne die Gravitation
Nichts geht ohne die Gravitation
![]() Proton- Proton Reaktion
Proton- Proton Reaktion
![]() Der CNO- Zyklus
Der CNO- Zyklus
![]() Der 3-Alpha Prozess
Der 3-Alpha Prozess
![]() Kohlenstoffbrennen
Kohlenstoffbrennen
![]() Neonbrennen
Neonbrennen
![]() Sauerstoffbrennen
Sauerstoffbrennen
![]() Siliziumbrennen
Siliziumbrennen
![]() Verrücktes Gas
Verrücktes Gas
![]() Entstehung der Elemente
Entstehung der Elemente
Nichts geht ohne die Gravitation
Wohl schon immer haben sich die Menschen gefragt, was denn dieser helle Glutball am Himmel ist und was ihn leuchten und Wärme abstrahlen lässt. Kein Wunder, dass die Sonne in alten Kulturen zunächst als Gottheit verehrt wurde. Dann gab es tatsächlich auch Zeiten in denen man ernsthaft spekulierte, die Sonne müsse aus einem großen Berg brennender Kohle bestehen. Zum Glück ist das nicht der Fall, sonst wäre es hier auf der Erde inzwischen schon recht ungemütlich kühl geworden! Denn einerseits würde ein Kohlehaufen auch von der Masse der Sonne nur ein paar Millionen Jahre brennen, andererseits längst nicht die beobachtete Energie abstrahlen. Heute wissen wir, dass die nach außen abgestrahlten Energien eines Sterns in seinem Innern durch Verschmelzungen von Atomkernen freigesetzt werden.
Diesen Vorgängen wollen wir uns jetzt widmen.
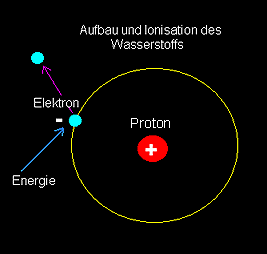
Komprimiert man Materie (z.B. die Luft beim Aufpumpen eines Fahrradschlauches), so werden die einzelnen Atome oder Moleküle näher zusammengebracht und sie werden sich schneller bewegen, weil sie dem Druck ausweichen wollen. Bewegung von Atomen/Molekülen ist aber nichts anderes als Wärme. Die Luftpumpe wird spürbar wärmer, und man kann sich vielleicht vorstellen, was der Druck bei großen Körpern wie der Erde oder gar der Sonne bewirkt. Steigt man in die Erde hinab, so wird es im Mittel nach jeweils 30 [m] um 1 [K] wärmer, im Zentrum herrschen dann vermutlich etwa 2000 bis 10000 [K] (der Temperaturanstieg verläuft allerdings nicht linear). In der Sonne ist alles naturgemäß noch viel krasser: in ihrer Zentralregion wie bei den meisten Sternen herrschen Temperaturen von rund 20 Millionen [K]! Massereichere Sterne können sogar noch viel höhere Temperaturen erreichen, wie wir noch sehen werden. Die Temperaturen sind deshalb so hoch, weil die nach innen gerichtete Gravitation das Sternzentrum gnadenlos zusammenquetscht und somit hoch komprimiert - ähnlich wie beim Fahrradschlauch. Unter solchen Verhältnissen ist dann jede Materie gasförmig und ionisiert, d.h. die Atome sind ihrer Elektronen vollständig beraubt.
Nebenstehende Grafik skizziert den Aufbau eines Wasserstoffatoms. Es besteht aus einem Proton, welches den Kern darstellt, und wird von einem Elektron in einer Elektronenhülle umkreist. Wird dem Elektron Energie zugeführt, z.B. in Form von Wärme oder eines Gamma- Quants, so verlässt es den Verbund und es bleibt ein ionisierter, positiv geladener Kern (das Proton) zurück.
Ein solches ionisiertes Gas nennt man Plasma. Die Atomkerne (hier: Wasserstoff, also Protonen) bewegen sich durch die hohe Temperatur so schnell, dass sie hin und wieder zusammenstoßen. Es kann dann geschehen, dass vier Wasserstoffkerne (Protonen) zu einem Heliumkern verschmelzen. Dabei tritt der so genannte Massendefekt auf - der Heliumkern ist komischerweise ein klein wenig leichter als die Summe aller Ausgangsprodukte! Doch genau das ist es, was die Sonne und alle anderen Sterne leuchten lässt! Dieser winzig kleine Verlust an Masse wird als Energie abgestrahlt. Bei einem einzigen gebildeten Heliumkern beträgt der Massendefekt nur etwa 1%, immerhin verliert die Sonne aber auf diese Weise in jeder Sekunde 4 Millionen Tonnen an Masse. Doch keine Sorge, auch in den nächsten 4 Milliarden Jahren kann sie das problemlos durchhalten.
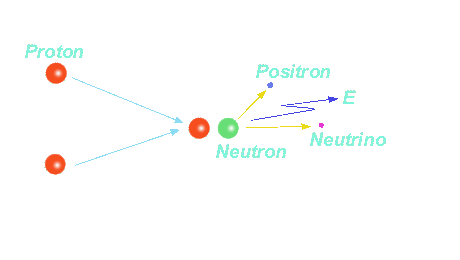
Im Temperaturbereich, in welchem Kernreaktionen ablaufen, sind keine Elektronen mehr an die Atomkerne gebunden. Die ihnen (in Form von Wärme) zugeführte Energie ist viel zu hoch, als dass die Atomkerne sie noch an sich binden könnten. Durch die Kontraktion interstellarer Materie steigt die Temperatur im Innern eines werdenden Sterns stetig an. Ab etwa 3 Millionen [K] kann die so genannte Proton- Proton- Reaktion einsetzen: zwei Wasserstoffkerne (1H+), von denen jeder nur aus einem (positiv geladenen) Proton besteht, stoßen zusammen und bilden unter Abgabe eines Positrons (e+, das positiv geladene Antiteilchen des Elektrons), eines Elektronneutrinos (νe) und von Energie (E = mc2, Massedefekt!) in Form eines Gamma- Photons () einen Deuteriumkern (2D):
2D+ bedeutet, dass der Wasserstoffkern nun aus 2 Kernteilchen, einem Proton und einem Neutron, besteht. Das neutrale Neutron wird in der oben gezeigten Reaktion dadurch erzeugt, weil eines der beiden Protonen ein Positron abspaltet. Deuterium, auch schwerer Wasserstoff genannt, stellt durch das zusätzliche Neutron ein Isotop des Wasserstoffs dar (die Schreibweise 2H+ ist daher ebenfalls korrekt). Bei dieser Startreaktion wird eine Energiemenge von 0,42 [MeV] freigesetzt. Das freigesetzte Positron reagiert sofort mit einem Elektron - beide vernichten (annihilieren) sich gegenseitig zu 2 Gamma- Quanten:
e+ + e- 2
Die bei dieser vollständigen Umwandlung von Materie freigesetzte Energiemenge beträgt 1,022 [MeV], so dass insgesamt 1,442 [MeV] Energie abgestrahlt werden. Zusätzlich trägt das Neutrino noch 0,26 [MeV] davon, hauptsächlich in Form von kinetischer Energie.
Doch halt, irgendetwas stimmt hier doch nicht! Ein Neutron ist schwerer als ein Proton, also muss das Deuterium schwerer sein als die beiden Protonen, aus denen es entstand. Wo bleibt dann der Massedefekt? Wieso wird überhaupt Energie freigesetzt? Es müsste doch Energie verbraucht werden! Des Rätsels Lösung liegt in der Bindungsenergie des neuen Atomkerns. Er stellt einen energetisch günstigeren Zustand dar und bei der Vereinigung von Proton und Neutron wird mehr Energie freigesetzt, als zur Bildung des Neutrons erforderlich ist. Interessant ist zudem, dass letzten Endes alle in einem Stern freigesetzte Energie umgewandelte Gravitation ist. Nur durch ihren Druck auf das Zentrum des Sterns werden die Atomkerne so energiereich, dass die Kernfusionen ablaufen können.
Wichtig zu wissen:
Man beachte, dass die hier genannten Kernverschmelzungen nur aufgrund eines Effektes der Quantenmechanik ablaufen können. Normalerweise sind auch bei den im Sterninnern herrschenden Temperaturen die elektrischen Abstoßungskräfte der Protonen so hoch, dass es nicht zu einer Kernverschmelzung kommen würde. Die Coulombkraft der beiden positiven elektrischen Ladungen würde eine Abstoßung verursachen. Die Protonen müssten also eine sehr hohe Geschwindigkeit haben, um diese Barriere zu überwinden. Nur wenige weisen aber eine solche kinetische Energie auf. Hier greift jedoch der so genannte Tunneleffekt. Ein Proton überwindet hin und wieder die Energiebarriere der elektrischen Abstoßung, indem es sie wie durch einen Tunnel durchdringt. Man kann sich das vorstellen wie einen Bergsteiger, der anstatt die Energie zum Übersteigen eines Berges aufzubringen, einfach durch einen Tunnel marschiert. Solche Durchtunnelungen finden nicht häufig statt, auch nicht in der Quantenwelt, durch die riesige Anzahl an Protonen gibt es aber genügend Kernverschmelzungen, um die Sterne leuchten zu lassen.
Auf diese PP- Reaktion (Proton-Proton) muss ein Proton etwa 14 Milliarden Jahre warten! Doch sind im Zentrum eines Sterns derart viele Protonen vorhanden, dass zu jedem Zeitpunkt unzählige dieser Zusammenstöße stattfinden und die fortdauernde Energiefreisetzung gewährleistet ist.
Das nun gebildete 2D+ reagiert nach nur 1,4 Sekunden mit einem weiteren Proton unter Abgabe eines Gamma-Quants () zu einem Heliumisotop:
Bei dieser Reaktion werden 5,49 [MeV] an Energie freigesetzt. Nun dauert es nochmals rund 1 Million Jahre, bis dieses 3He2+ mit einem weiteren seiner Art zu einem "richtigen" Heliumkern mit vier Kernteilchen (zwei Protonen und zwei Neutronen), wieder unter Energieabgabe, reagiert. Dabei werden 2 Protonen freigesetzt:
3He2+ + 3He2+ 4He2+ + 1H+ + 1H+
Auch hier wird wiederum Energie freigesetzt, 12,86 [MeV], weil das Helium nochmals einen energetisch günstigeren Zustand als die Ausgangsprodukte darstellt. Im Endeffekt vereinigen sich bei der PP- Reaktion demnach 4 Protonen unter Abgabe von 2 Elektron- Neutrinos und 2 Gamma- Quanten zu einem Heliumkern.
 Die freigesetzte Energie ist in Form kinetischer Energie, also als Bewegungsenergie der entstandenen Teilchen, sowie als Strahlung vorhanden. Bei der bisher beschriebenen PP- Reaktion wird eine Energiemenge von insgesamt 24,2 [MeV] freigesetzt, entsprechend rund 4 x 10-12 [J]. Sie wird auch PP- Reaktion I genannt, weil sie im Temperaturbereich ab etwa 10 Millionen [K] abläuft, wie es in der Sonne zu über 90% der Fall ist.
Die freigesetzte Energie ist in Form kinetischer Energie, also als Bewegungsenergie der entstandenen Teilchen, sowie als Strahlung vorhanden. Bei der bisher beschriebenen PP- Reaktion wird eine Energiemenge von insgesamt 24,2 [MeV] freigesetzt, entsprechend rund 4 x 10-12 [J]. Sie wird auch PP- Reaktion I genannt, weil sie im Temperaturbereich ab etwa 10 Millionen [K] abläuft, wie es in der Sonne zu über 90% der Fall ist.
Die Temperatur im Kern des nun aktiven Sterns steigt durch die freigesetzte Energie rapide an, das heißt der nach außen gerichtete (Bewegungs-) Druck der Gasteilchen würde zusammen mit dem Druck der entstandenen Strahlung den Stern förmlich zerreissen.
Solche thermalisierte Strahlung entsteht, wenn beispielsweise ein Elektron ein Gammaquant absorbiert und irgendwann diese aufgenommene Energie (E = hv) wieder abgibt, nun allerdings mit etwas erniedrigter Frequenz. Die Verringerung der Frequenz entsteht, weil das Elektron einen Teil der aufgenommenen Energie als Bewegungsenergie (thermische Bewegung!) verbraucht. Nach einiger Zeit wird das veränderte Quant vom nächsten Teilchen absorbiert und wiederum leicht verändert desorbiert usw., bis zum Schluss die ursprüngliche Gammastrahlung den Stern als sichtbares Licht verlässt.
Bei Temperaturen ab etwa 15 Millionen [K] treten weitere Nebenreaktionen auf, die als PP- Reaktion II bezeichnet wird:
1 Heliumisotop (3He2+) trifft auf einen Heliumkern (4He2+), es bildet sich ein Berylliumkern (7Be4+)
3He2+ + 4He2+ 7Be4+ +

Das 7Be4+ fängt ein Elektron ein und wird zu Lithium (7Li3+)
7Be4+ + e- 7Li3+ + νe
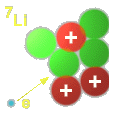
7Li3+ kollidiert mit einem Proton und bildet 2 4He2+- Kerne
7Li3+ + 1H+ 4He2+ + 4He2+
Nur noch etwa 9% der Fusionen in der Sonne laufen nach diesem Schema ab, wobei 18,9 [MeV] an Energie freigesetzt werden. Erreicht ein Stern Temperaturen von mehr als 23 Millionen [K] in seinem Zentrum, finden hauptsächlich Fusionen des Typs PP- Reaktion III statt:
Ein Heliumisotop 3He2+ bildet wieder mit einem 4He2+ einen Berylliumkern 7Be4+
3He2+ + 4He2+ 7Be4+ +
Das 7Be4+ kann auch ein Proton einfangen und wird zum Borisotop (8B5+)
7Be4+ + 1H+ 8B5+ +
Dieses 8B5+ gibt ein Neutrino und ein Positron ab und zerfällt in zwei 4He2+- Kerne
8B5+ 8Be4+ + e+ + νe
8Be4+ 4He2+ + 4He2+
Bei dieser Reaktion, die in der Sonne nur noch einen Anteil von 0,1 % hat, wird noch eine Energie von 1,7 [MeV] freigesetzt. Die entstandenen Neutrinos durchqueren ungehindert den gesamten Stern, weil sie kaum mit anderen Kernteilchen wechselwirken. Im PP- III- Prozess sind die Neutrinos am energiereichsten und lassen sich damit am besten in den Detektoren nachweisen.
Ist im Stern bereits ein geringer Anteil an Kohlenstoff (C) vorhanden, so tritt ab etwa 10 Millionen [K] eine zusätzliche Fusionsmöglichkeit des Wasserstoffs zu Helium auf, bei welcher der Kohlenstoff eigentlich nur als Katalysator fungiert. Nach ihren Entdeckern Hans Bethe und Carl Friedrich von Weizsäcker wird der CNO- Zyklus (Kohlenstoff, Stickstoff, Sauerstoff) auch Bethe-Weizsäcker- Zyklus genannt:
Ein Kohlenstoffkern 12C fängt ein Proton 1H ein und bildet ein instabiles Stickstoffisotop 13N
12C + 1H 13N +
13N zerfällt unter Abgabe eines Positrons und Neutrinos zu 13C
13N 13C + e+ + νe
13C nimmt ein Proton 1H auf und bildet Stickstoff 14N
13C + 1H 14N +
14N nimmt ein Proton 1H auf und bildet ein Sauerstoffisotop 15O
14N + 1H 15O +
15O zerfällt unter Abgabe eines Positrons und Neutrinos zu 15N
15O 15N + e+ + νe
15N fängt ein Proton 1H ein und bildet wieder Kohlenstoff 12C und einen Heliumkern 4He
15N + 1H 12C + 4He

Auch in dieser Reaktion wird wieder Energie freigesetzt, und zwar ein Betrag von 25,03 [MeV]. Wie leicht zu erkennen ist, dient der Kohlenstoff nur als Katalysator, im Endeffekt verschmelzen 4 Protonen zu einem Heliumkern. Während eine vollständige Proton- Proton- Reaktion einige Milliarden Jahre in Anspruch nimmt, benötigt der CNO- Zyklus 340 Millionen Jahre und ist damit deutlich schneller. Es liegt auf der Hand, dass eine solche Fusion in den ersten Sterngenerationen (= Population III) nicht ablaufen konnte. Einfach deshalb, weil es damals noch keinen Kohlenstoff gab.
Ist der Wasserstoff im Kern zu Helium fusioniert, wird damit auch keine Energie mehr freigesetzt. Der bislang herrschende Strahlungs- und Gasdruck lässt nach und es gibt keine Gegenwehr zu den nun überhand nehmenden Gravitationskräften. Diese quetschen die jetzt überwiegend aus Heliumkernen (α- Teilchen) bestehende Zentralregion zusammen, worauf die Temperatur weiterhin kräftig ansteigt. Hierdurch dehnt sich der Stern aus, die Sternhülle kühlt sich durch die nun gigantische Oberfläche ab - der Stern tritt ins Stadium eines Roten Riesen.
Durch die voranschreitende Kontraktion und den damit weiter ansteigenden Druck entartet das Gas im Kern, in Abhängigkeit von der Gesamtmasse des Sterns (siehe auch weiter unten Verrücktes Gas ). Durch den Entartungsdruck wird jetzt aber eine weitere Kontraktion unterbunden, nur noch die Temperatur erhöht sich.
Ab 100 Millionen [K] beginnt das Heliumbrennen, bei dem Heliumkerne zu Kohlenstoff verschmelzen. Der Ausdruck "Brennen" ist ein wenig unglücklich gewählt, denn das Helium "verbrennt" nicht in einer chemischen Reaktion, sondern hier fusionieren Atomkerne. Die Heliumfusion wird auch nach ihrem Entdecker Edwin Salpeter als Salpeter- Prozess bezeichnet. Durch die nun wieder freigesetzte Energie dehnt sich der Kern aus und die Entartung wird durch die weiter ansteigende Temperatur zurückgenommen. Das Heliumbrennen zündet explosionsartig und wird daher als Helium- Blitz (Helium- Flash) bezeichnet (siehe hierzu auch Entstehung und Entwicklung der Sterne):
2 Heliumkerne 4He bilden zunächst Beryllium 8Be unter Abgabe eines Gammaquants. Dieser Vorgang benötigt sogar einen kleinen Energiebeitrag (92 [keV]):
4He + 4He 8Be +
Der Berylliumkern 8Be fusioniert mit einem Heliumkern 4He unter Abgabe von Energie zu Kohlenstoff 12C:
8Be + 4He 12C +
Das gebildete 8Be ist dabei aber sehr instabil und zerfällt rasch wieder (nach 10-16 [s]) in 2 4He. Nur ein sehr geringer Anteil des Berylliums, etwa jeder zehnmilliardste Kern kommt wirklich zur Fusion mit einem Heliumkern. Damit dieser Prozess tatsächlich abläuft, müssen 3 Alpha- Teilchen praktisch fast gleichzeitig zusammenstoßen. Daher der Name 3-Alpha-Prozess, in welchem 7,27 [MeV] an Energie freigesetzt werden.
Derartige Reaktionen können nur unter extrem hohen Drucken und Temperaturen stattfinden und sind deshalb ausschließlich in Sternen mit genügender Masse möglich. Die Wahrscheinlichkeit für das synchrone Zusammentreffen dreier Heliumkerne ist sehr gering und somit konnte bei der Elemententstehung nach dem Urknall kein Kohlenstoff erzeugt werden, denn die Temperatur war dazu viel zu schnell abgesunken.
Manchmal trifft ein Alpha- Teilchen auch auf einen Kohlenstoffkern (12C), wobei unter Entsendung eines Gamma- Quants Sauerstoff (16O) entsteht.
12C + 4He 16O +

Während des Heliumbrennens wird in einer Schale um den Kern weiter Wasserstoff fusioniert, was einerseits stabilisierenden Strahlungsdruck liefert und die Kernregion mit frischem Brennstoff versorgt. Die Sternenhülle kontrahiert wieder, die Oberfläche wird heißer. Doch die Leuchtkraft sinkt trotz wieder verkleinerter Oberfläche, weil der Stern insgesamt weniger Energie freisetzt. In der ruhigen Phase des Heliumbrennens befinden sich beispielsweise die Riesen Aldebaran und Arktur (Spektralklasse K).
Hat ein Stern eine Masse von mindestens 4 Sonnenmassen, so kann auch nach dem Ende des Heliumbrennens noch Energie freigesetzt werden. Zunächst aber kontrahiert der Stern wieder, bis das Gas in der Kernregion auf 2 x 108 [kg/m3] verdichtet ist (ein Stück Würfelzucker würde hier 200 [kg] wiegen!) und eine Temperatur von 600 Millionen [K] angenommen hat. Jetzt kann der Kohlenstoff fusionieren:
12C + 4He 16O +
13C + 4He 16O + n
Die Fusion des Kohlenstoffisotops 13C stellt somit eine Neutronenquelle dar, auch bei der folgenden zweiten Fusion wird ein Neutron freigesetzt:
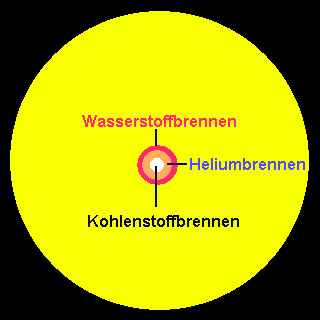
12C + 12C 23Mg + n
12C + 12C 23Na + 1H
12C + 12C 20Ne + 4He
12C + 12C 16O + 2 4He
Mit diesen Neutronen können im s- Prozess weitere Elemente gebildet werden. Bei den Reaktionen, in denen 23Mg und 16O entstehen, wird keine Energie freigesetzt, sondern sogar ein wenig verbraucht. Nach einer relativ kurzen Zeit - einige Tausend Jahre - ist das Kohlenstoffbrennen beendet. Der Kern besteht jetzt aus Magnesium, Sauerstoff und Neon. Selbst letzteres kann unter geeigneten Bedingungen in einem weiteren Schritt Energie freisetzen.
Sterne mit einer Mindestmasse von 8 Sonnenmassen können im Anschluss an das Kohlenstoffbrennen auch noch ihr Neon fusionieren. Nach dem Ende der C- Fusionen versiegt wieder einmal der Energienachschub aus dem Zentrum (wenn auch in den Schalen um den Kern weiter Helium bzw. Wasserstoff fusionieren). In dieser Folge setzen erneut Kontraktionen ein, die das Sternzentrum zu einer ungeheuren Dichte von 4 Milliarden [kg/m3] zusammenpressen. Die Temperatur steigt dabei auf unvorstellbare 1200 Millionen Kelvin. Unter diesen Bedingungen werden die Gammaphotonen überaus energiereich und sie sind jetzt imstande, zuvor erbrütete Kerne durch Fotodissoziation zu zerschlagen.
So wird mancher Neonkern zu Sauerstoff und Helium zertrümmert:
20Ne + 16O + 4He
Ist das geschehen, kann ein anderer Neonkern mit dem nun wieder zur Verfügung stehenden Helium verschmelzen und dabei erneut Energie freisetzen:
20Ne + 4He 24Mg +
Der Neon- Kern kann jedoch auch ein Neutron einfangen und dabei Energie freisetzen. Das gebildete Neonisotop kann dann wieder mit einem α- Teilchen reagieren, wobei wieder ein Neutron freigesetzt wird:

21Ne + 4He 24Mg + n
Aus den Reaktionen geht hervor, dass im Laufe dieser Fusionen das Neon in die Elemente Sauerstoff und Magnesium umgewandelt wird, sich das Sternzentrum also damit anreichert. Nach dem Verbrauch des Neons erlischt abermals die Energieversorgung aus dem Zentrum. Wenn auch in Schalen um den Kern jetzt noch Kohlenstoff, Helium und Wasserstoff fusionieren, reicht doch die freigesetzte Energie nicht aus, den weiteren Kollaps aufzuhalten. Das Sternzentrum wird nochmals durch die Gravitation verdichtet.
Und zwar geht die Verdichtung jetzt so weit, bis eine Temperatur von 1½ Milliarden [K] und eine Dichte von 10 Milliarden [kg/m3] erreicht ist. Unter diesen Bedingungen kann eine Reihe von Reaktionen der Sauerstoffkerne ablaufen, wobei vor allem Silizium, Phosphor und Schwefel gebildet werden:
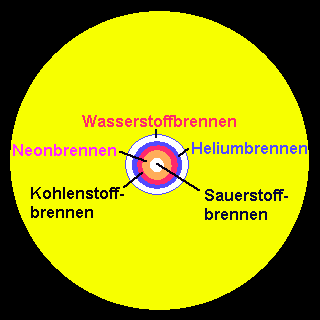
16O + 16O 31S + n
16O + 16O 31P + 1H
16O + 16O 28Si + 4He
16O + 16O 24Mg + 2 4He
Es dauert nur wenige Jahre, bis aller Sauerstoff im Sternzentrum verbraucht ist. Wieder setzen anschließend Kontraktionen ein, bis die Bedingungen geschaffen sind, dass nun auch noch als letzte Phase das Silizium fusioniert.
Die Temperatur muss jetzt mindestens auf 2,7 Milliarden [K] gestiegen sein und die Dichte auf 30 Tonnen (!) pro [cm3], damit das Siliziumbrennen einsetzen kann. Es ist das letzte Mal, dass ein Stern (von mindestens 8 Sonnenmassen) noch einmal für ein paar Tage in einem stabilen hydrostatischen Gleichgewicht in seinem Zentrum Energie freisetzt. In Schalen um den Kern fusionieren derweil weiterhin Sauerstoff, Neon, Kohlenstoff, Helium und Wasserstoff.
Während des Siliziumbrennens fusionieren zwei Siliziumkerne zu einem Nickelisotop:
28Si + 28Si 56Ni +
Das Nickelisotop ist jedoch nicht stabil und zerfällt alsbald in einem β+- Zerfall unter Abgabe eines Positrons und eines Elektronneutrinos zu Kobalt:
56Ni 56Co + e+ + νe
Doch auch das Kobalt ist nicht stabil und zerfällt wiederum, diesmal zum stabilen Eisenkern:
56Co 56Fe + e+ + νe
Am Ende befindet sich im Sternzentrum eine Eisenkugel von vielleicht 10 000 [km] Durchmesser mit einer maximalen Masse von ca. 2,8 bis 3 Sonnenmassen.
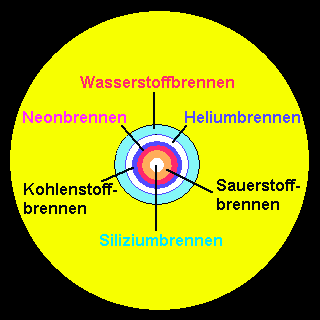
Jetzt kann die Gravitation noch einmal das Sternzentrum verdichten, ohne jedoch auf eine Gegenwehr zu stoßen. Das Eisen (56Fe) wird durch einen Photodissoziation genannten Prozess in 14 Heliumkerne (4He) gespalten, verursacht durch hochenergetische Gammaphotonen, die in den umliegenden Schalen produziert wurden und nun in den Kern eindringen. Dies führt zum sofortigen Kollaps des Sternzentrums. Bei diesem Kollaps kann der Druck so hoch ansteigen, dass die Bindungsenergie der Kernbausteine verringert wird und sich die Atomkerne praktisch auflösen. Die so freigesetzten Protonen fangen ein Elektron ein (inverser Betazerfall) und bilden damit ein Neutron. Womit dann der gesamte Kern fast ausschließlich aus Neutronen besteht. Das ist die Geburtsstunde eines Neutronensterns, bei genügend großer Masse auch eines stellaren Schwarzen Lochs.
Bei den Temperaturen, die in einem Stern, ja selbst auf seiner Oberfläche herrschen, kann keine Materie in festem oder flüssigem Zustand bestehen. Unter diesen Bedingungen können nur Gase existent sein, wenn sie auch ganz und gar nicht die Eigenschaften besitzen, welche wir von unserer Umgebung gewohnt sind. So sind unter Normalbedingungen die Atome bzw. Moleküle der Gase elektrisch neutral, weil genau so viele (negative) Elektronen in der Elektronenhülle den Atomkern umgeben, um die positive Ladung der Protonen zu neutralisieren.
Bei hohen Temperaturen, ab 10 000 [K], verlassen jedoch die ersten Elektronen das Atom, weil die zugeführte (kinetische) Energie so groß wird, dass ein Aufenthalt in der Hülle nicht mehr möglich ist. Dadurch wird das Atom natürlich elektrisch (positiv) geladen, weil die Ladung der Protonen nicht mehr vollständig neutralisiert wird. Das Gas ist ionisiert. Und zwar umso mehr, je weniger Elektronen sich in der Elektronenwolke aufhalten. Ein solches Gas nennt man Plasma. Das geht soweit, dass im Sterninnern kein Atom mehr ein Elektron besitzt. Nun leistet die Gravitation ihren Beitrag: sie presst das Gas immer mehr zusammen, je tiefer man in den Stern eindringt. So liegt die Gasdichte im Außenbereich bei vielleicht 5 [gcm-3], während sie im Kern eines massereichen Sterns leicht um den Faktor 10 Millionen verstärkt wird. Entsprechend hoch ist damit auch der Druck des Gases.
Den Gasdruck kann man sich vorstellen als die Häufigkeit und Heftigkeit, mit der die Gasmoleküle in einem geschlossenen Gefäß gegen die Gefäßwandung prallen; mit ansteigendem Druck geschieht dies häufiger und heftiger. In einem Stern übernimmt dabei die Gravitation die Funktion der Gefäßwandung.
Im Sterninnern kommt noch ein wichtiger Faktor hinzu, der Strahlungsdruck. Das Verhalten der Strahlungsphotonen (ein Photon ist die kleinste Energieeinheit einer beliebigen elektromagnetischen Schwingung, man kann auch sagen ein Strahlungsquant) kann man sich in Analogie zu den gerade beschriebenen Molekülen vorstellen.
Strahlungs- und Gasdruck würden jeden Stern unweigerlich auseinander reißen, wenn die Gravitation die Materie nicht mit gnadenlosem Griff zusammenpressen würde.
Bedingt durch die ungemütlichen Bedingungen im Sterninnern, also extremer Gas- und Strahlungsdruck sowie höllischer Temperatur, müssen sich alle Atome und was von ihnen übrig geblieben ist, alle Teilchen der Materie mit sehr großer Geschwindigkeit bewegen. Normalerweise ist diese Geschwindigkeit abhängig von der Temperatur (Temperatur ist ja nichts anderes als Bewegung von Teilchen) und dem Druck. Bei sehr hohen Dichten wie im Kern eines Sterns spielt die Temperatur hierbei aber keine Rolle mehr. Vielmehr ist die hohe Geschwindigkeit darin begründet, dass die Teilchen extrem nahe zusammengequetscht sind.
Nun können aber nicht gleiche Teilchen (Elektronen, Protonen oder Neutronen; Teilchen mit gleichem Spin, das ist der Eigendrehimpuls) gleiche Lagen und Geschwindigkeiten einnehmen (Pauli- Verbot), sie können sich nicht beliebig einander nähern, sondern müssen sich durch ihren Impuls unterscheiden. Das erreichen sie, indem sie sich schnell bewegen. Je höher die Dichte, umso höher ist die Geschwindigkeit, und umso größer sind dann auch die Geschwindigkeitsdifferenzen. Ein solches Gas nennt man entartet.
Mit zunehmender Dichte entarten zuerst die Elektronen, bis ihre Geschwindigkeit in den relativistischen Bereich (d.h. in der Nähe der Lichtgeschwindigkeit) gelangt. Steigt der Druck weiter, vereinigen sich die Elektronen mit den Protonen, es entsteht ein Neutronenstern. Auch dieses Neutronengas entartet mit weiter steigender Dichte, und ab 1014 [gcm-3] bewegen auch sie sich im relativistischen Bereich. Weiteres zur Entartung unter Zustandsgleichung und Entartung.
Nun noch eine tabellarische Darstellung, wann und unter welchen Umständen die verschiedenen chemischen Elemente im Universum erzeugt werden bzw. wurden:
Legende:
p = Proton
n = Neutron
γ = Gammaquant
e- = Elektron
e+ = Positron
ve = Elektron- Neutrino
MJ = Jupitermassen
MS = Sonnenmassen
D = Deuterium
T = Tritium
| Elemente | Ursprung - Quelle - Prozess | Bedingungen - Reaktionen | Weitere Abläufe - Endstadien | ||
|---|---|---|---|---|---|
| p ↔ n | 0,01s < t < 1s | 10 MeV < T < 1 MeV | p und n im therm. Gleichgewicht | Zeit nach Urknall | |
| H+ | T ≈ 1 MeV, t ≈ 1s, p + n, Paarvernichtung abgeschlossen | Neutrinos koppeln ab 1010 K | Bei 0,5 MeV Paarvernichtung: Elektronen/Positronen | n/p ≅ 1/7 (Betazerfall) |
|
| D T He Li Be | T ≈ 80 KeV, t ≈ 1 min p + n ↔ D + γ | T + n → D + γ D + D → T + p D + p → 3He + γ D + D → 3He + n T + D → 4He + n | T + α → 7Li + γ 3He + n → p + T 3He + D → p + 4He 3He + α → 7Be + γ 7Li + p → 4He + α 7Be + n → 7Li + p | ||
| H He | 5 min: Ende primordialer Synthese 4He ist stabil, kein Zerfall mehr | Erzeugte Materie besteht jetzt aus: | 75% H ~25% He 0.001% D Spuren Li, T, 3He | ||
| Li Be B | 4He + 3H → 7Li + γ | 4He + 3He → 7Be + γ Aber: 7Be + e- → 7Li + γ | Li, Be und B werden überwiegend in Spallationsreaktionen der Interstellaren Materie erzeugt | Ende der Elementerzeugung im frühen Kosmos | |
| C, O, Si, N..Au.. Pt | Pop-III-Sterne (erste Generation) Lebensdauer 3- 4 Mill. Jahre Bis 1000 MS | Überwiegend C und O werden erbrütet | Erzeugung höherer natürlicher Elemente (s- Prozess) | Sternende jedoch als Paarinstabilitäts- SN (r-, p- und rp- Prozess) Weitere Elemente | Völlige Zerstörung der Sterne |
| He | Brauner Zwerg < 8% MS 13 MJ75 MJ ≈ 0,07 MS | D + p → 3He (ab 13 MJ) ab ≈ 2 Mill. K: 7Li + p → 4He (ab 65 MJ) | CH4 in Sternatmosphäre | Nach Fusionsende Abkühlung in 10- 50 Mill. Jahren | |
| He | Roter Zwerg > 8 - 57% MS | p-p-Reaktion ab ≈ 3 Mill. K Gesamte Brenndauer: | 4 1H → 4He Reaktion im Kern Mehrere 10 Mrd. bis 100 Mrd. | Anschließend noch Schalenbrennen 4 1H → 4He bis 1 Billon Jahre! | Keine weiteren Elemente, Ende: Weißer Zwerg |
| He (C, O?) | Kühle Unterzwerge 2000-6000 K Oberflächentemperatur | H- Brennen | Alte Pop-II- Sterne | Halo der Galaxis | |
| He C, O | Heiße Unterzwerge > 10 000 K Oberfläche | He- Brennen | Nur noch dünne H- Schale vorhanden | Verlust der Hülle | Kern eines Roten Riesen |
| He | Zwergstern ∼ 1 MS (Gelber Zwerg) | Kern ab T ≈ 5 x 106 K (Sonne = 1.5 x 107 K) : 4 1H → 4He pp- Reaktion + CNO-Zyklus | Nach 9,4 Mrd. Jahren Schale aus 4 1H → 4He Kern besteht nur noch aus He | Nach 12,3 Mrd. Jahren He- Blitz: Kern: He → C | Zwergsterne: 0.3 bis 2.3 MS Beispiel: Sonne |
| C | Zwergstern ∼ 1 MS T ≈ 108 K | Heliumbrennen 3 4He → 12C + γ | Schale: H- Fusion | Heliumbrennen möglich ab 0.3 MS | |
| O | Zwergstern ∼ 1 MS T ≈ 1.5 x 108 K | Kern: C, O Keine weitere Fusion | He- Schalenbrennen | Stern expandiert zum Roten Riesen | |
| He, C, O | Rote Riesen ∼ 1 - 8 MS | Kern: C, O entartet, keine weitere Fusion | He- Schalenbrennen H-Schalenbrennen | Nach Schalenbrennende Abstoßen der Hülle → Weißer Zwerg | AGB- Sterne |
| Mg, Na, Ne, O | Rote Riesen > 4 MS T > 6 x 108 K | 12C + 4He → 16O + γ 12C + 12C → 24Mg + γ 12C + 12C → 23Mg + n 12C + 12C → 23Na + 1H 12C + 12C → 20Ne + 4He 12C + 12C → 16O + 24He | C- Brennen ist Neutronenquelle! | Vorhandenes Fe wird durch s- Prozess in höhere Elemente umgewandelt | |
| Cu, Zn, Ge, Ga, As, Se, Br, Kr, Zr, Y, Sr, Rb | s- Prozess in kohlenstoffbrennenden Sternen Langsamer Neutroneneinfang | 209Bi + n → 210Bi + γ 210Bi → 210Po + e- + ve 210Po → 206Pb + 4He 206Pb + 3 n → 209Pb 209Pb → 209Bi + e- + ve | Maximal erreichbare Kerngröße: 209Bi | Stabile Isotope | |
| He, C, O, Ne, Na, Mg, S, P, Si, Fe | Rote Überriesen ∼10 - 40 MS Blaue Riesen ∼20 - 40 MS Blaue Überriesen > 40 MS Hyperriesen > 100 MS | T ≈ 1.2 x 109 K: Ne- Brennen (Fotodesintegration!)
20Ne + γ → 16O + 4He | T ≈ 1.5 x 109 K: O- Brennen
16O + 16O → 32S + γ | T ≈ 2.7 x 109 K: Si- Brennen
28Si + 28Si → 56Ni + γ | Je nach Status noch fusionierende Schalen aus H, He, C, Ne, O (von außen nach innen gesehen) |
| He, C, O, Si, S, Fe | Supernova
SN Ia (Weißer Zwerg) | 1. Deflagration 2. Detonation | 56Ni → 56Co + e+ + ve 56Co → 56Fe + e+ + ve | Hoher Si- Anteil | Völlige Zerstörung |
| Elemente bis Massezahl ∼ 260 | Supernova SN II r- Prozess Schneller Neutroneneinfang | Neutronenreiche Kerne Photodesintegration | Fe, Pb, Bi, U, Th, Pu | p- Prozess langsamerProtoneneinfang schneller Protoneneinfang | Neutronenstern Schwarzes Loch |
| ∼ 6000 Isotope im Kosmos (vermutet) | 300 bekannte stabile Kerne 2500 bekannte instabile Kerne 3500 unbekannte instabile Kerne | s- Prozess liefert stablie Kerne bis 209Bi | r-Prozess führt zu neutronenreichen Kernen, hier setzt Photodesintegration ein | p- und rp- Prozesse führen zu protonenreichen, instabilen Kernen, Photodesintegration | © Werner Kasper 11/2010 |