Der Raum

Was ist Raum?

Das, was wir heute unter Raum verstehen, entstand erst mit dem Urknall. Und mit diesem Ereignis begann auch die Zeit, es war die Geburtsstunde unseres Kosmos. Wir wissen heute, dass vor etwa 13,7 Milliarden Jahren alle Materie des Kosmos wahrscheinlich aus einem Punkt unendlicher Dichte entstand, so sagt es uns das Standardmodell des Urknalls. Erst mit der explosionsartigen Ausdehnung konnte sich der uns geläufige Raum entfalten. Aufgrund unserer Beobachtungen ist es nicht möglich auf Ereignisse zu schließen, die vor diesem Zeitpunkt stattfanden. Deshalb ist es völlig sinnlos darüber zu spekulieren, was vor diesem Zeitpunkt gewesen sein könnte. Denn Ereignisse vor dieser unserer Zeit können in keiner Weise einen Einfluss auf die Entwicklung des Universums haben, und so ist die Frage, ob es vorher schon Raum (oder Zeit) gab, absolut unbeantwortbar. Verschiedene Hypothesen deuten zwar darauf hin, dass unser Universum aus einer Fluktuation, einer plötzlichen Schwankung des Zustandes eines übergeordneten Universums ("Multiversum", "Hyperraum") entstand. Was immer man darunter verstehen mag, bleibt dies vorerst nicht mehr als Spekulation. Hier wollen wir nun versuchen, ein wenig "Licht" in das Wesen des uns scheinbar so vertrauten Raums zu bringen.

Einstein formulierte einmal: Da wo Materie oder Energie ist, da ist auch Raum. Oder anders betrachtet: Erst durch die Anwesenheit von Materie und Energie bnt sich der Raum auf. So kam er auch zur folgerichtigen Feststellung:

Ein Raum ohne jegliche Materie ist sinnlos!

Eine weitere seiner Definitionen ist: Raum ist da, wo sich Licht bewegt (und Zeit ist, wie lange es sich bewegt). Seit EuklidEuklid von Alexandria, griechischer Mathematiker, beschrieb das Parallelenaxiom, den euklidischen Algorithmus (größter gemeinsamer Teiler), bewies Unendlichkeit der Primzahlen. (300 v. Chr.) wissen wir, dass eine Gerade die kürzeste Verbindung zwischen zwei Punkten ist. Und bis zum Beginn des 20. Jahrhunderts war man überzeugt, dass zwei Geraden als Parallele unendlich weit ins Universum verlaufen, ohne sich je zu schneiden. Deshalb sollte sich auch das Licht im Kosmos absolut geradlinig ausbreiten. Doch stimmt dies immer noch?

Die drei Dimensionen des euklidischen Raums stellt man im so genannten kartesischen Koordinatensystem dar. Alle 3 Raumachsen (Länge, Breite, Höhe) stehen senkrecht aufeinander. Jede Achse stellt eine Gerade dar, die sich grundsätzlich unendlich weit ins All erstreckt. Nehmen Sie sich einmal ein großes Blatt Papier, ein Lineal und einen Bleistift. Nun zeichnen Sie eine hübsche Gerade auf und überlegen einmal, ob diese auch wirklich gerade ist. Denken Sie dabei an die Gestalt unseres Planeten...

Sicher sind Sie auch zu dem Ergebnis gekommen, dass diese schöne Gerade eigentlich eine "Krumme" sein müsste, denn wenn das Lineal lang genug wäre, würde nach rund 40 000 [km] die "Gerade" exakt wieder in ihren Ausgangspunkt laufen. Sie hätte dann nämlich die Erde umrundet und wäre ein Kreis! Jede Gerade, die wir auf der Erdoberfläche ziehen, ist Teil eines (Groß-) Kreises und man nennt sie deshalb nicht "Krumme", sondern Geodäte (siehe hierzu auch Krumme Sachen).

Halten wir also fest, dass Raum nur dort ist, wo auch Materie und/oder Energie anwesend sind, und wo sich Licht ausbreiten kann. Das aber gilt für unser gesamtes Universum! Gibt es denn nun überhaupt Geraden und damit Parallelen? Im Prinzip nicht, denn sie sind nur in einem Raum ohne Materie möglich. Jede Anwesenheit von Materie aber krümmt den Raum und daher muss alles was sich im Raum bewegt diesen Krümmungen folgen, selbst das Licht. Das Bild eines absolut euklidischen Raums sollte man also tunlichst aufgeben. Das gilt vor allem in Bereichen hoher Massedichten, in der Umgebung von Neutronensternen oder gar Schwarzen Löchern wirken sich die Raum(zeit)krümmungen z.T. verheerend aus. Großräumig gesehen, beispielsweise in den riesigen Leerräumen des Universums, spielen die Krümmungen keine bedeutende Rolle. Wir können sie vernachlässigen und von einer euklidischen, flachen Raumzeit ausgehen, solange wir von großen Skalen sprechen.

Sir Isaac Newton hatte seinerzeit den Raum als absolut bezeichnet, womit er meinte, dass der Raum durch nichts und niemand beeinflussbar und damit unveränderlich ist. Wir werden noch sehen, dass diese Aussage nicht mehr haltbar ist.

Minkowski- Raum

Hermann Minkowski (1864-1909), wie schon im Abschnitt über die Zeit angedeutet, war einer von Einsteins Professoren und ein sehr bedeutender deutscher Mathematiker seiner Zeit.

Unter vielen anderen Arbeiten ist er besonders bekannt geworden durch die Einführung einer vierten Dimension in den euklidischen Raum, weshalb man ihn heute kurzerhand als Minkowski- Raum bezeichnet.

Wenn in einer Nachbargalaxie eine Supernova explodiert, so werden wir erst dann eine Information über dieses Ereignis bekommen, wenn das Signal (Licht) die Distanz zu uns überbrückt hat. Das Licht (die Information) bewegt sich mit der Geschwindigkeit $c$ durch den Raum und benötigt dazu die Zeit $t$ . Damit ist $c \cdot t$ also die zeitliche Distanz des Ereignisses von unserem Standpunkt aus und genau genommen eine Entfernungsangabe! Diese hat Minkowski als vierte Dimension $w$ in den dreidimensionalen euklidischen Raum eingeführt und ist damit die Zeitdimension umgangen: $w = c \cdot t$ . Ist so etwas gerechtfertigt? Wir wissen doch, dass alle unsere Empfindungen, unser Herzschlag, jedes Ereignis in unserem Leben in exakter zeitlicher Abfolge stattfinden. Das alles spielt sich in unserem Erfahrungsraum mit den 3 uns vertrauten Raumkoordinaten $x, y, z$ ab. Nun soll noch eine Raumkoordinate hinzukommen, und die Zeit wird nicht mehr berücksichtigt?

Genau so ist Minkowski mit seiner neuen Ansicht des Raumes verfahren. Durch die Verwendung der vierten Dimension $w$ braucht man nicht mehr die Zeit, um ein Ereignis im dreidimensionalen Raum zu beschreiben, sondern man gibt nur den Ort im vierdimensionalen Minkowski- Raum an. Folgendes, aus dem "harten" Leben gegriffene Beispiel mag dies verdeutlichen:

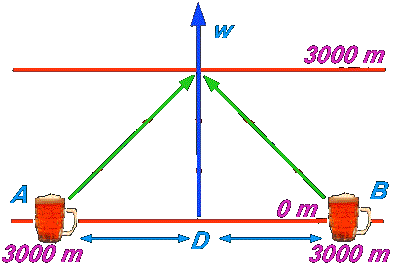
Ein Wanderer, nennen wir ihn treffend D (= durstig), irrt orientierungslos durch die Wüste und ist dem Tod durch Verdursten nah. Glücklicherweise melden sich auf seinem Handy gleich zwei Kneipenwirte, A und B, die jeweils genau 3 [km] von seinem Standort entfernt sind und bereits gezapft haben. Weil die Funkwellen sich mit Lichtgeschwindigkeit ausbreiten, treffen beide Signale (grüne Pfeile) den Wanderer, wenn er sich auf der

w

- Koordinate im Punkt

w = 3000 [m]

befindet. In dem Moment, als beide Wirte das Bier fertig haben und die SMS gleichzeitig senden, befindet sich der Wanderer im Punkt D, hier aber sind beide Signale noch 3000 [m] von ihm entfernt. Er kann sie erst empfangen, wenn er sich im Minkowski- Raum auf der Koordinate

w

3000 [m] weiter bewegt hat.

Wir erkennen, dass eine Zeitangabe zur Beschreibung dieses (wichtigen) Ereignisses keinesfalls erforderlich ist!

Anmerkung:
Es ist hier nicht gefragt, für welchen Wirt sich der Wanderer entscheidet!

Man kann also durchaus die Zeit und den Ort eines Ereignisses durch eine (vierdimensionale) Ortsangabe beschreiben.

Wir leben in einem für uns verständlichen dreidimensionalen Erfahrungsraum und können uns sicher nicht vorstellen, wie dieser sich nach Minkowskis Ansicht mit Lichtgeschwindigkeit durch den vierdimensionalen Minkowski- Raum bewegt (selbst die umgekehrte Betrachtung ist erlaubt, dass der vierdimensionale Minkowski- Raum sich mit Lichtgeschwindigkeit durch unseren 3-dimensionalen Raum bewegt!). Wir können nichts wahrnehmen, was nicht momentan in unserem "Gegenwartsraum" existiert. Unser dreidimensionaler Raum bewegt sich entlang der

w

- Koordinate durch den Minkowski- Raum. Dargestellt sind nur 2 Dimensionen als Fläche. Wenn dieser dreidimensionale Raum einen bestimmten Punkt auf der

w

- Koordinate schneidet, findet ein Ereignis statt. Genau das ist unser "Gegenwartsraum", der in diesem Moment dieselbe

w

- Koordinate hat wie der Minkowski- Raum. Alles, was darüber liegt, ist die Zukunft, unterhalb des Punktes liegt die Vergangenheit.

Vielleicht ist diese Art der Darstellung des Minkowski- Raums etwas anschaulicher. Dargestellt sind nur 2 Koordinaten,

x

und

c t = w

. Die Winkelhalbierende zwischen diesen Koordinaten

(x = c t)

entspricht dabei der Ausbreitung des Lichts. Diese Art der Darstellung nennt man Lichtkegel. Wenn man das Diagramm der Realität entsprechend gestaltet, und das ist hier der Fall, wird die zeitartige Achse (

c t

) in Sekunden unterteilt und die Raumachse (

x

) in Lichtsekunden (die Strecke, die das Licht in 1 s zurücklegt, also 300 000 [km]). Die Winkelhalbierende entspricht dann den so genannten Weltlinien von Photonen, sie steigen in einem Winkel von 45° an. Größer kann dieser Winkel niemals werden, sonst hätten die Teilchen mehr als Lichtgeschwindigkeit! Alles, was sich außerhalb dieser Weltlinien befindet, bleibt für immer unerreichbar. Ereignisse, die dort stattfinden nennt man raumartig. Innerhalb der blauen Kegel liegen die zeitartigen Ereignisse. Sie können in irgendeinem Zusammenhang stehen, weil innerhalb der Kegel gilt

x < c t

, was einfach bedeutet, dass sich nichts schneller als das Licht bewegt. Außerhalb der Kegel gilt

x < c t

, dieses "Irgendwo" ist für uns nicht mehr fassbar. Die Gegenwart liegt auf dem Schnittpunkt von

x / c t

, alles was oberhalb ist liegt in der Zukunft, unterhalb geht es in die Vergangenheit. Eingezeichnet ist noch eine Weltlinie, z.B. die eines Teilchens oder Menschen, welche sich mit unterschiedlicher Geschwindigkeit durch den Minkowski- Raum bewegen.

Vielleicht hat Minkowski bei der Bezeichnung des nach ihm benannten Raums einen Fehler gemacht, als er ihn nämlich ein raum- zeitliches Kontinuum nannte. Haben wir doch gesehen, dass es sich bei der vierten Dimension um eine Längenangabe, und nicht um eine Zeitangabe handelt. Vielleicht war es jedoch auch Absicht von Minkowski als auch von Einstein, dass sie den Begriff beibehielten, weil dieser "Irrtum" keine praktische Auswirkung hat.

Raumzeit

Verlassen wir nun Minkowskis Raum und wenden uns wieder Einsteins vierdimensionaler Raumzeit zu. Wie schon oben erwähnt, ist nach unserem alltäglichen Empfinden der Raum dreidimensional, man kann durch jeden Punkt im Raum drei senkrecht zueinander stehende Koordinaten ziehen (Länge, Breite, Höhe), es ist ein euklidischer Raum. Albert Einstein hat uns in seiner Allgemeinen Relativitätstheorie jedoch gezeigt, dass Raum und Zeit untrennbar miteinander zur vierdimensionalen Raumzeit verbunden sind.

Das ist im Grunde auch sehr einleuchtend und leicht zu verstehen: Stellen Sie sich einmal ein Universum ohne Zeit vor. Es wäre völlig fremdartig, denn darin gäbe es keine Entwicklung, ja man sagt, ein solcher Kosmos hat keine Geschichte! Nichts könnte sich hier bewegen, Wolken aus Gas und Staub könnten nicht zu Sternen kontrahieren, es gäbe weder Planeten noch Leben. Viel schlimmer noch, nicht nur dass es absolut finster und kalt wäre (es gäbe ja weder Licht noch Wärmebewegung von Molekülen), selbst Materie könnte nicht existieren. Denn die Elektronen um jeden Atomkern sind in ständiger Bewegung, das aber wäre in einem Universum ohne Zeit nicht möglich.

Weil in der Raumzeit alle 4 Dimensionen gleichberechtigt sind, denken wir uns nun einmal anstatt der Zeit eine der Raumdimensionen weg. Es könnten in einem solchen Kosmos demnach nur zweidimensionale Wesen auf einem zweidimensionalen Planeten leben. Diese "Flachländer" würden also nur eine Länge und eine Breite kennen, sie könnten weder Wolkenkratzer bauen noch bequem im Fernsehsessel sitzen. Höher entwickelte Lebewesen mit einem durchgehenden Verdauungstrakt würden einfach auseinanderfallen! Es sei denn, sie hätten die unappetitliche Variante entwickelt, bei welcher verdaute Nahrung denselben Weg nimmt wie die frische Kost. Wollten diese Wesen aneinander vorbei kommen, müssten sie übereinander kriechen, aber selbst das wäre schon ungeheuer problematisch ohne die Raumdimension "Höhe". Zumal ein Fortbewegungsapparat wie z.B. Beine, Flossen oder Flügel kaum denkbar wäre, der in 2 Dimensionen funktioniert. Es wäre sicher ein beschwerliches Leben in einem Kosmos, dem nur eine der vier Dimensionen fehlt. Diese Beispiele halten uns vor Augen, dass die 3 Raumdimensionen wie auch die Zeit untrennbar und gleichberechtigt miteinander verbunden sind und wir auch auf jede einzelne unbedingt angewiesen sind.

Krümmungen

Finden wir uns also damit ab, in einer vierdimensionalen Raumzeit zu leben. Sie wird allerdings durch die Anwesenheit von Materie gekrümmt, und zwar umso mehr, je größer die Masse ist. Nun muss alles, was sich in der Raumzeit bewegt, diesen Krümmungen folgen, selbst das Licht. Es kann nicht einfach geradeaus laufen, wie man vielleicht im ersten Moment vermuten würde.

Diese Voraussage der Einstein'schen Relativitätstheorie sollte zugleich auch den ersten Beweis für deren Richtigkeit liefern. Im März 1919 wurden dazu gleich 2 Expeditionen unternommen, um die stattfindende totale Sonnenfinsternis zu beobachten. Laut Einstein sollte man nämlich einen Stern nahe am Sonnenrand in einer etwas anderen Position vorfinden, als wenn man ihn nachts beobachtet. Einfach aus dem Grund, weil das Licht des Sterns den durch die Sonnenmasse verursachten Raumzeitkrümmungen folgen muss. Man fand tatsächlich die von Einstein vorausgesagten Positionsabweichungen! Seitdem wurden ungezählte Experimente unternommen und noch nicht ein einziges Ergebnis gefunden, welches an der Relativitätstheorie zweifeln ließe.

Raumzeitkrümmungen fallen naturgemäß gering aus bei Körpern kleiner Masse. Unsere Erde, erst recht der Mond, sind solch kleine Massen mit geringem Gravitationsfeld. Sie verursachen daher kaum nachweisbare Krümmungen. Anders sieht es bei extrem großen Massen aus, die über entsprechend starke Gravitationskräfte verfügen.

Ihren Sieg über alle anderen Naturkräfte feiert die Gravitation bei den Schwarzen Löchern. Hier herrscht an deren Ereignishorizont eine Gravitationsgewalt, welche die umgebende Raumzeit in sich selbst krümmt. Das bedeutet (zumindest bei nichtrotierenden Schwarzen Löchern) ein kugelförmiges Gebilde, welches das Loch vom restlichen Universum vollkommen abschneidet. Man kann sich dabei die Raumzeit auf 2 Dimensionen reduziert vorstellen, als ein gebntes Tuch, auf das man eine schwere Kugel legt. Das Tuch wird nach unten immer mehr ausgebeult (gekrümmt), in der Spitze endlich umschließt die Raumzeit das Schwarze Loch vollständig.

Aber wie verhält es sich dann mit den Raumzeitkrümmungen auf großen Skalen?

Wie bereits oben angedeutet, kann man bei relativ kurzen Distanzen bequem von einem euklidischen Raum sprechen. Den Strich auf unserem Blatt Papier sehen wir ohne Reue als Gerade an. Aber machen Sie den Spaziergang um die Erde und schon werden Sie sehen, dass es keine Geraden gibt! Einen Laserstrahl, auf den Mond gerichtet, können wir ebenfalls durchaus als Gerade akzeptieren. Auch noch, wenn wir größere Distanzen im Kosmos betrachten, hier ist die Materiedichte und damit die Krümmung nur gering. Doch ein (Super-) Laserstrahl, zum "Ende" des Universums gesendet, wird allen Raumzeitkrümmungen folgen und vielleicht irgendwann zu uns zurückkehren. Man mag sich hierzu vereinfacht das Universum als riesigen Luftballon vorstellen, es ist vollständig in sich selbst gekrümmt. Darin gibt es nichts "Gerades", denn jede Linie muss diesen Krümmungen gehorchen.

Raumstauchung!

Alle bisherigen Betrachtungen haben wir als ruhende Beobachter gemacht. Aber nun wollen wir uns fragen, was passiert mit dem Raum, wenn man sich schnell bewegt? Um das zu verstehen, benutzen wir wieder unsere Photonen- Uhr, bestehend aus 2 Spiegeln und einem Photon, die wir schon im Abschnitt über die Zeitdilatation kennen lernten:

Für die folgende Betrachtung ist es günstiger, dass wir die Uhr um 90° drehen. Den Weg, den das Photon von einem zum anderen Spiegel zurücklegt, wollen wir

b

nennen. Da im folgenden Abschnitt ein wenig Mathematik eine Rolle spielen wird, können Sie diese Erklärungen bei Nichtinteresse auch überschlagen und gleich weiter unten mit dem Lesen fortfahren.

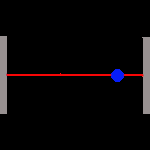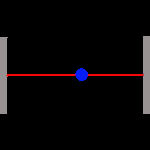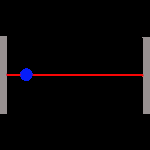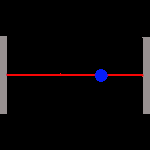
Unsere Präzisionsuhr funktioniert prächtig, und so werden wir nun ein Exemplar in die Rakete unseres überstrapazierten Astronauten einbauen und ihn wieder einmal auf die Reise schicken. Die Uhr ist so angebracht, dass sich das Photon längs zur Flugrichtung bewegt und wir die Uhr beobachten können. Eine baugleiche Lichtuhr haben wir natürlich neben uns auf der Erde.

Zunächst beobachten wir, wie sich das Photon vom linken Spiegel in Flugrichtung bewegt. Es benötigt die Zeit

t

, um bis zum rechten Spiegel zu gelangen, wobei es natürlich mit der Lichtgeschwindigkeit

c

fliegt. Wir erkennen, dass das Photon zusätzlich zu seinem Weg

b

auch die Bewegung der Rakete aufholen muss.

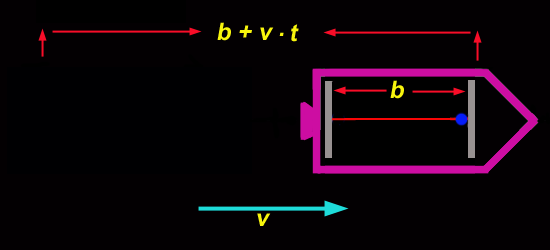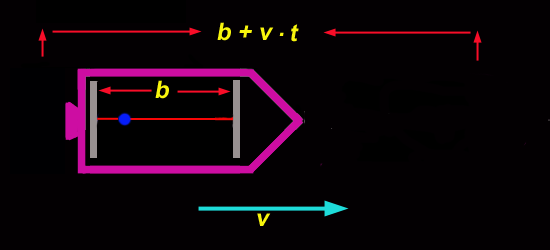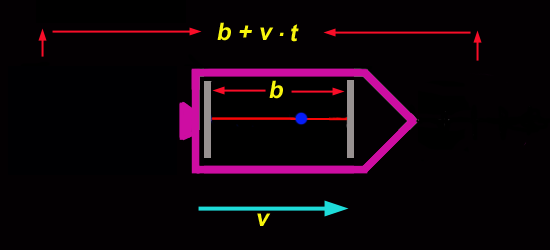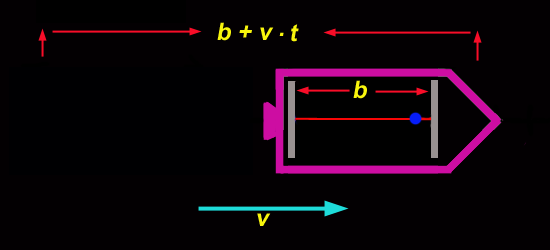
Die Rakete hat die Geschwindigkeit $v$ und der Gesamtweg des Photons ist daher $b + v \cdot t$ .

Die Flugzeit des Photons berechnet sich wie üblich aus dem Weg, dividiert durch die Geschwindigkeit, also:

$t = \frac{b}{c}$

Da sein Gesamtweg aber $b + v \cdot t$ ist, beträgt die von uns beobachtete Flugzeit

$t = \frac{b + v \cdot t}{c}$

Wir haben bis jetzt nur den Weg des Photons in Flugrichtung untersucht, auf dem Rückflug vom rechten zum linken Spiegel ergibt sich allerdings eine etwas andere Situation. Sehen wir uns noch mal die Rakete an:

Wenn das Photon vom rechten Spiegel startet, kommt ihm der linke Spiegel durch die Bewegung der Rakete entgegen. Dadurch verkürzt sich sein Weg, so dass sich dieser nun aus

b - v \cdot t

zusammensetzt. Weil die Zeit

t

nun eine andere Größe hat, nennen wir die Zeit für den Rückflug nun

t'

Analog zur obigen Rechnung ergibt sich nun für den Rückweg des Photons die Zeit

$t' = \frac{b - v \cdot t'}{c}$

Aus diesen Formeln können wir aber $t$ bzw. $t'$ nicht berechnen und müssen sie deshalb nach $t$ umstellen:

$t \cdot c = b + v \cdot t$

$t \cdot c - v \cdot t = b$

$t \cdot (c - v) = b$

$t = \frac{b}{c - v}$

und analog für den Rückweg

$t' = \frac{b}{c + v}$

Damit sind wir nun in der Lage, die Gesamtflugzeit - nennen wir sie $t_{G}$ - auszurechnen:

$t_{G} = t + t'$

Nun können wir schreiben:

$t_{G} = \frac{b}{c - v} + \frac{b}{c + v}$

Lassen wir unseren Astronauten einen Moment allein durchs All fliegen und sehen uns noch mal näher unsere eigene Photonenuhr an:

Wir haben ja eine baugleiche Uhr wie unser Astronaut, aber sie ruht. Weil das Photon keinen zusätzlichen Weg wie in der bewegten Rakete zurücklegen muss, ist die Berechnung der Zeit für den Hin- und Rückweg viel einfacher. Zur besseren Unterscheidung nennen wir jetzt den Weg unseres Photons

b_{E}

(

E

für Erde) und die Zeit, die es für beide Strecken braucht,

t_{E}

Die Zeit, die das Photon für den Hin- und Rückweg benötigt ist dann ganz einfach:

$t_{E} = \frac{2 b_{E}}{c}$

Im Abschnitt über die Zeitdehnung haben wir bereits gesehen, wie man die Zeit der schnell bewegten Rakete gegenüber unserer eigenen Zeit korrigieren muss, nämlich mit dem $γ$ - Faktor. Die Gesamtflugzeit des Photons in der Rakete $t_{G}$ berechnet sich demnach wie folgt:

$t_{G} = \frac{1}{\sqrt{1 - {(\frac{v}{c})}^{2}}} \cdot t_{E}$

In diese Gleichung können wir jetzt die oben gefundenen Ausdrücke einsetzen und erhalten als Ergebnis:

$\frac{b}{c - v} + \frac{b}{c + v} = \frac{1}{\sqrt{1 - {(\frac{v}{c})}^{2}}} \cdot \frac{2 b_{E}}{c}$

Unser Ziel ist zu untersuchen, wie sich der Weg des bewegten Photons verhält. Dazu müssen wir die gefundene Gleichung nach $b$ umstellen. Hierzu klammern wir zuerst $b$ auf der linken Seite aus:

$b (\frac{1}{c - v} + \frac{1}{c + v}) = \frac{1}{\sqrt{1 - {(\frac{v}{c})}^{2}}} \cdot \frac{2 b_{E}}{c}$

...und bringen die Brüche auf den gemeinsamen Hauptnenner...

$b \cdot \frac{c + v + c - v}{(c - v) (c + v)} = \frac{1}{\sqrt{1 - {(\frac{v}{c})}^{2}}} \cdot \frac{2 b_{E}}{c}$

...den Bruch auf der linken Seite fassen wir weiter zusammen...

$b \cdot \frac{2 c}{c^{2} - v^{2}} = \frac{1}{\sqrt{1 - {(\frac{v}{c})}^{2}}} \cdot \frac{2 b_{E}}{c}$

um ihn nun auf die rechte Seite zu bringen, wo wir die 2 kürzen können und c zusammenfassen...

$b = \frac{c^{2} - v^{2}}{c^{2}} \cdot \frac{1}{\sqrt{1 - {(\frac{v}{c})}^{2}}} \cdot b_{E}$

Wenn man den ersten Bruch auf der rechten Seite auflöst, kommt man zu folgendem Bild:

$b = (1 - {(v / c)}^{2}) \cdot \frac{1}{\sqrt{1 - {(\frac{v}{c})}^{2}}} \cdot b_{E}$

Den Ausdruck $1 - {(v / c)}^{2}$ kann man auch als Produkt zweier Quadratwurzeln darstellen:

$b = \sqrt{1 - {(\frac{v}{c})}^{2}} \cdot \sqrt{1 - {(\frac{v}{c})}^{2}} \cdot \frac{1}{\sqrt{1 - {(\frac{v}{c})}^{2}}} \cdot b_{E}$

So dass wir jetzt eine Wurzel kürzen können:

$b = \sqrt{1 - {(\frac{v}{c})}^{2}} \cdot b_{E}$

Aus dem Abschnitt über die Zeitdilatation haben wir ja bereits den Gamma- Faktor kennen gelernt

$\frac{1}{\sqrt{1 - {(\frac{v}{c})}^{2}}} = γ$

Womit wir jetzt eine recht einfache und bequeme Form haben, den Weg des bewegten Photons zu berechnen:

$b = \frac{1}{γ} \cdot b_{E}$

Was sagt uns nun eigentlich die gefundene Formel? Sie gibt uns eine Aussage darüber, dass dieselbe Strecke, wenn man sich mit relativistischer Geschwindigkeit in Bezug auf ein ruhendes System bewegt, viel kürzer erscheint! Der Weg des Photons in der Rakete hat eine weit geringere Länge als diejenige des Photons in unserer irdischen Lichtuhr. Alle Längen, die wir in Flugrichtung der Rakete messen, sind gestaucht. Die Größe der Stauchung ist direkt abhängig von der Geschwindigkeit und wird durch den Gamma- Faktor beschrieben. In Analogie zur Zeitdilatation bedeutet dies, dass wir bei Bewegung mit relativistischen Geschwindigkeiten in gleichen Zeiten viel größere Strecken zurücklegen.

Gibt es denn quer zur Flugrichtung auch eine Stauchung? Nein, denn in dieser Richtung ist die Geschwindigkeit ja gleich Null. Wenn man das in unsere Korrekturformel für die Länge einsetzt, ergibt sich:

$\frac{1}{γ} = \sqrt{1 - {(\frac{0}{c})}^{2}} = 1$

In dieser Raumrichtung gibt es damit keinen Korrekturfaktor, die Stauchung findet nur in Flugrichtung statt.

So wird unser geplagter Astronaut die Erde sehen, wenn er der Lichtgeschwindigkeit näher kommt. Je größer seine Geschwindigkeit, umso "schmaler" wird er die Erde sehen. Aber wieso schrumpft sie nicht komplett, in allen Raumrichtungen? Wir haben ja die Uhr des Astronauten in Flugrichtung beobachtet und gesehen, dass nur in dieser Richtung eine Stauchung erfolgt. Wenn wir die Breite der Rakete messen bzw. der Astronaut die "Breite" der Erde, finden beide dieselben Werte als wenn sie sich in Ruhe befänden.

Man darf nun allerdings nicht glauben, dass sich alle schnell bewegten Gegenstände in ihrer Größe verkleinern.

Aus unserer Sicht macht der tapfere Astronaut zwar eine "relativistische Diät", aber leider spürt er selbst nichts davon. Das, was wir von ihm sehen, ist nicht eine Schrumpfung seines Körpers, sondern eine Stauchung der Raumzeit! Nicht sein Körper wird schmaler, was wir sehen ist eine Schrumpfung der Maßstäbe. Derselbe Zollstock, der auf der Erde 1 [m] anzeigt, zeigt uns das auch in der Rakete des Astronauten, aber er hat eine andere, viel kürzere Länge als hier bei uns.

Auch in seiner Flugrichtung sieht der Astronaut die Raumzeit gestaucht vor sich, je schneller er fliegt, umso kürzer werden seine Wege. Das hat auch einen Einfluss auf seine "Sicht der Dinge": Sein Sehfeld wird immer schmaler, alle Sterne rücken in seinem Sichtkegel immer näher zusammen, je schneller er fliegt.

Ähnlich wie bei unseren Feststellungen, dass es keine "universelle" Zeit im Kosmos gibt, also in jedem unterschiedlich bewegten Bezugssystem die Zeit anders verläuft, verhält es sich auch mit dem Raum. Raum ist genau wie die Zeit eine reine Privatangelegenheit, es gibt keinen absoluten Raum.

Jeder Beobachter im Kosmos hat damit eine andere Sicht der Dinge. Denn in der Regel wird sich jedes Bezugssystem im All unterschiedlich verhalten, so dass jeder Beobachter andere Entfernungen und Abmessungen wahrnimmt, wie er auch andere Zeitverläufe misst.

Nun abschließend noch einmal zum Begriff Raum: Stellen Sie sich vor, jemand würde das Universum über Nacht ausräumen. Was bliebe übrig? Nur Raumzeit? Nein, eigentlich absolut nichts! Ohne die Materie, ohne Sterne, Strahlung, Gas, Staub und Atome gäbe es keinen Raum. Raum ist eine Bezeichnung für alle Abmessungen, alle Entfernungen zu irgendwelchen Objekten. Wenn Sie das Innenleben Ihres Computers komplett ausräumen (wovon dringend abgeraten wird), befindet sich NICHTS mehr in dem Gehäuse (abgesehen von der Luft), Sie können darin nichts mehr lokalisieren. Allerdings belehrt uns hier wieder mit einem kräftigen Einspruch die Quantenphysik: sie sagt, es gibt kein "leeres" Vakuum, keinen leeren Raum, denn ständig entstehen in diesem so genannte virtuelle Teilchenpaare. Das Vakuum ist ein brodelnder See ständig neu entstehender und sich wieder vernichtender Teilchen. Der Raum ist also aus Sicht der Quantenphysik etwas völlig anderes. Ja, auf der Quantenebene wird womöglich sogar die Raumzeit selbst einem ständigen Auf und Ab unterliegen, so genannten FluktuationenZufällige Änderung oder Schwankung einer ansonsten bekannten konstanten oder schwingenden Systemgröße.. Sie wird dann nicht mehr so ruhig und glatt sein, wie wir sie bis jetzt sahen, sondern eher eine schaumartige, unruhige Struktur haben.

Schwenkt man, wo wir gerade dabei sind, von den gigantischen kosmischen Entfernungen in den Mikrokosmos, so kommt man zur Frage: Gibt es eigentlich auch eine kleinste Ausdehnung? Bereits Werner Heisenberg hat diese Frage bei der Entwicklung der Quantentheorie aufgegriffen und eine "kleinste Länge" postuliert. Darunter versteht man eine gequantelte Länge L₀, die es nicht gestattet, kleinere Abstände zu messen. Danach sind auch nur ganzzahlige Vielfache von L₀ zulässig.

Heute verwendet man die so genannte Planck- Wheeler- Länge, um die kleinste mögliche Ausdehnung aufzuzeigen. Sie hat die unvorstellbar kleine Länge von nur 10^-35[m]. Das ist quantenphysikalisch die kleinste noch sinnvolle Distanz.