Die Zeit

Raumzeit

Maße

Anfang oder Ende?

Zeitdehnung

Zeit ist Privatsache

Das GPS- System

Raumzeit

Zeit ist eine Dimension, für die wir kein Sinnesorgan besitzen. Daher haben wir ein nur subjektives Zeitempfinden, welches sich nach der biologischen Uhr richtet und damit vom Tagesablauf abhängt. Physikalisch gesehen beschreibt sie den temporären Ablauf eines Ereignisses. Isaac Newton formulierte seinerzeit:

"Es gibt eine absolute, wahre und mathematische Zeit, die gleichförmig für sich und vermöge ihrer eigenen Natur fließt, ohne Beziehung zum äußeren Geschehen".

Wie sehr sich Newton mit dieser Aussage irrte, wissen wir spätestens seit der Entwicklung der Relativitätstheorie durch Minkowski, Lorentz und natürlich Einstein. Minkowski fügte dem dreidimensionalen Raum die Zeit hinzu, auf

"dass von nun an Raum und Zeit für sich völlig zum Schatten herabsinken, nur noch eine Union der beiden soll Selbstständigkeit bewahren".

Die Relativitätstheorie wie auch die Quantenmechanik bringen nun zusätzlich den Beobachter bei Betrachtung des Raumzeit- Kontinuums mit ins Spiel. Denn die Bewertung von Zeit oder Raum fällt unterschiedlich aus, wenn sich Beobachter mit unterschiedlichen Geschwindigkeiten bewegen. Dazu später aber noch mehr.

Jedes Ereignis im Kosmos ist definiert durch die Raumkoordinaten und die Zeitkoordinate. Fehlt nur eine davon, ist das Ereignis nicht mehr korrekt zu beschreiben. Ohne die Zeitkoordinate aber hätte unser Universum überhaupt keine Geschichte, es gäbe keine Entwicklung, es wäre ein totes Universum, weil kein einziges Ereignis stattfinden könnte. Kein Stern, kein Planet würde sich bilden und erst recht kein Leben entstehen. Alles, was wir in unserem Leben erfahren, ist eine ununterbrochene Kette von Ereignissen! Den Verlauf der Zeit betrachten wir als gleichförmig fließend:

Unterbrechungen im Zeitfluss scheint es nicht zu geben, augenscheinlich ist es eine Dimension ohne "Ecken" oder "Zacken". Dennoch haben wir durch die Quantenmechanik erkennen müssen, dass auch die Zeit in kleinsten Abschnitten einer gewissen Unschärfe unterliegt.
Wir können also heute nicht mehr die Zeit vom Raum losgelöst betrachten. Die Relativitätstheorie macht deshalb auch keinen Unterschied mehr zwischen den 4 Koordinaten "Länge, Breite, Höhe und Zeit". Dennoch soll hier die Zeit als eigenständige Größe betrachtet werden.

Maße

Die Einteilung der Zeit in messbare Abschnitte erfolgt rein willkürlich. Wenn wir alltägliche Begriffe wie Stunde oder Sekunde verwenden, sollten wir uns darüber im Klaren sein, dass sich diese Einheiten aus unserer natürlichen Umgebung ableiten. Unsere Zeiteinteilung ist gegeben durch die Erddrehung (Stunde Minute, Sekunde), die Dauer des Erdumlaufs um die Sonne (Jahr) und die Dauer des Mondumlaufs (Monat, Woche). Wesen auf anderen Planeten mit anderen Umlaufzeiten werden sicherlich eine völlig abweichende Zeiteinteilung haben. Um einen reproduzierbaren Maßstab für die Zeit herzustellen, braucht man lediglich eine bestimmte Menge des Metalls Cäsium (¹³³Cs), dessen Atome durch eine spezifische Umlagerung sich gegenseitig zur Ausstrahlung von Mikrowellenstrahlung anregen. Mit dieser Welle versetzt man dann einen Quarzkristall in Schwingungen, welche nun durch eine elektronische Digitalanzeige dargestellt werden. Genau
9 192 631 770 Schwingungen dieser Mikrowelle benötigt man zur exakten Darstellung eines Zeitraums von einer Sekunde, welche die Basiseinheit der Zeitmessung bildet. Dieses Prinzip ist in einigen Tausend Atomuhren weltweit verwirklicht. Darüber hinaus senden einige dieser Uhren regelmäßige Radioimpulse aus, so dass wir jederzeit bei einem Blick auf unsere Funkuhr höchst präzise wissen, was die Stunde geschlagen hat.

Weil man die Lichtgeschwindigkeit heute recht genau bestimmen kann und diese im Vakuum eine universelle, absolut unveränderliche Naturkonstante darstellt, verwendet man sie in den SI- Einheiten zur Definition der Basiseinheit Sekunde. Demnach wird eine Sekunde als die Zeit definiert, die ein Lichtstrahl benötigt um eine Strecke von 299 792 458 [m] zu durcheilen. Ebenso wird heute die Längenangabe nicht mehr wie früher auf das in Paris aufbewahrte Urmeter zurückgeführt, sondern auf eine Zeitangabe. 1 Meter entspricht der Strecke, die ein Lichtstrahl in 1/299 792 458 [s] durcheilt. Diese Angabe ist viel genauer als das Urmeter, weil die Lichtgeschwindigkeit nicht wie die Länge des Urmeters von der Temperatur abhängig ist.

Zeit fließt augenscheinlich kontinuierlich in eine Richtung, ohne jede Unterbrechung. Vermutlich kann sie dies unendlich lang, jedenfalls so lange wie unser Universum existiert. Wie aber sieht es im kleinsten Bereich aus? Gibt es vielleicht eine kleinste Zeiteinheit? Ja, in der Physik rechnet man mit der so genannten Planckzeit, dem kleinsten noch sinnvollen Zeitabschnitt. Er leitet sich aus folgender Beziehung ab:

$t_P=\sqrt{\frac{\mathrm{\hslash }G}{c^5}}\approx \mathrm{5,39121}·{10}^{-44}s$

Hierin ist $G$ die Gravitationskonstante, $\mathrm{\hslash }$ die Planck- Konstante über 2 Pi und $c$ die Lichtgeschwindigkeit. In diesen winzigen Bereichen ist auch die Zeit der Unschärfe der Quantenmechanik unterworfen, man kann sie nicht mehr erfassen, weiß nicht ob sie vorwärts oder rückwärts läuft und sie wird durch die Beobachtung in ihrer Richtung beeinflusst. Durch keine auch noch so ausgeklügelte Methode ist es möglich, einen derart kurzen Zeitabschnitt zu messen. Hierzu wäre ja ein Apparat notwendig, der in noch kleineren Zeiteinheiten messen könnte, um eine halbwegs genaue Zeitbestimmung durchzuführen. Doch kürzere Zeiten sind nicht möglich.

Anfang oder Ende?

Man kann sich nun die Frage stellen: Hat die Zeit einen Anfang, und gibt es vielleicht auch ein Ende? Den ersten Teil der Frage kann man mit einem klaren "Ja" beantworten. Die Zeit unseres Kosmos begann mit dem Urknall. Das war, zumindest für unser Universum, der absolute Punkt Null (genau genommen beginnt unser All mit der oben genannten Planckzeit, was davor war liegt verschwommen in der Quantenunschärfe). Wir wissen nicht, wie und woraus der Kosmos entstand, ob er vielleicht nur ein Staubkorn in einem "Multiversum" ist, in welchem völlig andere Gesetze gelten und eventuell eine für uns unbegreifliche Zeit existiert. Jedenfalls ergeben sich für den Verlauf unserer Zeit lediglich zwei Alternativen: Sie kann ein Ende nehmen, wenn irgendwann in ferner Zukunft das gesamte Universum wieder kontrahieren sollte durch die Eigengravitation. Es wird dann vollständig in sich zusammenstürzen, alle Materie, Energie, Raum und Zeit in einem schier unendlich kleinen Punkt (einer Singularität?) vereinen. Das wäre das Ende von Allem, auch der Zeit. Falls wir im Gegensatz zu einem solch geschlossenen Universum in einem offenen leben (und alles deutet bisher darauf hin), so wird die Expansion des Raums unendlich lang fortgesetzt. Selbst wenn dann irgendwann alle Materie zerfallen ist und der Kosmos nichts Sinnvolles mehr enthält, wird es noch die Zeit geben.

Zeitdehnung

Bis jetzt haben wir die Zeit als gleichmäßig in eine Richtung fließend betrachtet. Durch Einsteins Relativitätstheorie wissen wir aber, dass Zeit abhängig ist vom Bezugssystem eines Beobachters. Zeit lässt sich nämlich beeinflussen, und zwar durch Gravitation und durch Bewegung:

Je schneller die Bewegung oder je größer die Gravitation, umso langsamer verläuft die Zeit.

So wird z.B. eine Atomuhr an Bord eines in 10 km Höhe fliegenden Flugzeugs nachweislich schneller laufen als auf dem Erdboden, denn hier unten ist die Gravitation größer (man kann das durchaus nachmessen). Selbst die Kirchturmuhr geht schneller als unsere Armbanduhr, der Unterschied ist aber noch verschwindend gering. Tragen wir unsere Uhr in die Nähe eines Schwarzen Loches, so wird sie durch die extreme Gravitation immer langsamer laufen, je näher wir diesem Objekt kommen. Kommt sie so nahe an das Loch, dass sie den Ereignishorizont berührt, bleibt die Zeit gänzlich stehen. Noch verrückter: womöglich läuft sie innerhalb des Ereignishorizontes sogar rückwärts!

So verhält es sich auch bei unserem "armen Astronauten" (der inzwischen ja schon so manches Schwarze Loch besuchen musste), wenn er sich mit hoher Geschwindigkeit bewegt. Für ihn vergeht die Zeit viel langsamer als für das Bodenpersonal auf der Erde. Hätte er ein Superraumschiff, mit dem er die Lichtgeschwindigkeit erreichen könnte (was natürlich nicht möglich ist), so würde für ihn die Zeit stehen bleiben! Er könnte dann in Nullzeit jeden beliebigen Punkt im Universum erreichen.

Wie aber wird er aus seiner Sicht die Vorgänge auf der Erde beobachten? Der Astronaut kann mit Fug und Recht von sich behaupten, selbst der ruhende Pol im Universum zu sein. Nach seiner Anschauung steht er still im Raum und die Erde sowie das restliche All fliegen an ihm vorüber! Während seine Borduhr (auch seine biologische Uhr) vollkommen normal läuft, sieht er die Zeit auf der Erde nun immer langsamer verlaufen, je schneller er sich bewegt. Daran erkennt man, dass Zeit an unterschiedlichen Orten, oder besser gesagt in unterschiedlich bewegten Bezugssystemen anders verläuft:

Es gibt im Universum keinen absoluten Ort, den man als ruhenden Bezugspunkt bezeichnen kann, und deshalb ist die Zeit an verschiedenen Orten unterschiedlich.

Zeit ist also abhängig von der Bewegung des betrachteten Bezugssystems. Wie aber kommt Einstein zu solchen Aussagen? Um das zu verstehen, stellen wir uns eine simple, aber hochgenaue Uhr her. Sie besteht ganz einfach aus zwei parallelen Spiegeln, zwischen welchen ein Photon hin und her reflektiert wird. Als Maßeinheit der Zeit verwenden wir dabei die Dauer, die das Photon für den Weg vom einen zum anderen Spiegel benötigt. Weil die Lichtgeschwindigkeit absolut konstant ist, arbeitet unsere Uhr mit höchster Präzision:

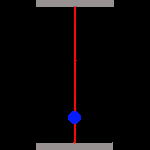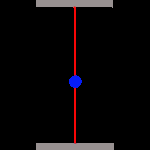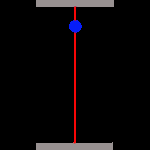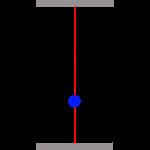
Jetzt können wir auf den Feuerknopf drücken und unseren Astronauten ins All schießen. Er dreht erst ein "paar Runden" um Geschwindigkeit aufzunehmen, und fliegt dann mit relativistischer Geschwindigkeit (in deutlichen Bruchteilen der Lichtgeschwindigkeit) auf einem solchen Kurs, dass wir bequem seine Uhr beobachten können. Was werden wir sehen?

Minkowski, Einsteins ehemaliger Professor (der seinen Studenten Einstein noch als "faulen Hund" bezeichnete), erkannte in dessen Gleichungen die Bedeutung des Satzes des Pythagoras, der die Seitenverhältnisse eines rechtwinkligen Dreiecks beschreibt:

$A^2+B^2=C^2$

Das Photon durcheilt nun alle Strecken mit der Lichtgeschwindigkeit $c$, also $A$ und auch $C$. Somit können wir sagen, dass sich die Strecken $A$ zu $C$ verhalten wie die Zeiten $T$ zu $\mathrm{T\text{'}}$:

$A/C=T/\mathrm{T\text{'}}$

Während das Photon $C$ durchläuft, verschieben sich die Spiegel mit der Geschwindigkeit $v$ um den Betrag $B$, daher gilt auch

$B/C=v/c$

Nun wollen wir untersuchen, wie sich die Laufzeiten zueinander verhalten. Wir beginnen damit, den Satz des Pythagoras durch $C^2$ zu dividieren:

${\left(\frac{A}{C}\right)}^2+{\left(\frac{B}{C}\right)}^2=1$

Wir bringen $B/C$ auf die andere Seite:

${\left(\frac{A}{C}\right)}^2=1-{\left(\frac{B}{C}\right)}^2$

Um $A/C$ berechnen zu können, müssen wir auf beiden Seiten die Wurzel ziehen:

$\frac{A}{C}=\sqrt{1-{\left(\frac{B}{C}\right)}^2}$

Jetzt können wir die Verhältnisse $A/C$ und $B/C$ durch die anderen physikalischen Größen ersetzen, da sie ja einander proportional sind. Die Strecke $A$ ersetzen wir also durch $T$, die Zeit, die das Photon für einen Weg auf unserer Erduhr benötigt und $C$ durch $\mathrm{T\text{'}}$, die verlängerte Zeit in der Raumschiffuhr. Wie wir oben gesehen haben, verhalten sich $B/C=v/c$, und wir ersetzen daher auch diesen Ausdruck:

$\frac{T}{\mathrm{T\text{'}}}=\sqrt{1-{\left(\frac{v}{c}\right)}^2}$

Wir bilden noch den Kehrwert und erhalten eine damit eine bequeme Möglichkeit, die Größe der Zeitdehnung zu berechnen:

$\frac{\mathrm{T\text{'}}}{T}=\frac{1}{\sqrt{1-{\left(\frac{v}{c}\right)}^2}}=\gamma$

Dies ist nun der berühmte Gamma- Faktor, ein sehr wichtiger Ausdruck, der häufig in der Relativitätstheorie vorkommt. Er gibt uns an, um welchen Faktor sich die Zeit verlangsamt, wenn sich jemand im Gegensatz zu uns als ruhende Beobachter mit einer Geschwindigkeit $v$ bewegt. Das gilt für jede Bewegung! Selbst wenn wir einen Fußgänger an unserem Fenster vorbeigehen sehen, verläuft seine Zeit eine winzige Idee langsamer als unsere. Das ist aber kaum messbar, überhaupt bemerken wir auf der Erde nichts von der Zeitdehnung, sie ist einfach zu gering. Erst bei hohen Geschwindigkeiten wird sie deutlich spürbar, wie folgende Beispiele zeigen:

Man sieht an diesen Beispielen sehr deutlich, dass man die Zeitdehnung in unserem Alltag durchaus vernachlässigen kann, erst in relativistischen Geschwindigkeitsbereichen wirkt sie sich erheblich aus. Exakt bei Lichtgeschwindigkeit wird sie dann sogar unendlich groß!

Wenn Sie möchten, können Sie hier selbst den armen Astronauten mit seinem Raumschiff durch den Kosmos jagen - sofern Sie die Ausführung des folgenden Java- Scripts auf Ihrem Rechner zulassen. Die Geschwindigkeit wird in Bruchteilen der Lichtgeschwindigkeit eingegeben, z.B. 98% als 0.98. Dezimalstellen bitte nur mit Punkt eingeben, 100% = 1.0 sind nicht erlaubt, denn hier wird die Zeitdehnung unendlich! In großen Geschwindigkeitsbereichen wird das Script leider etwas ungenau:

Für den Astronauten geht seine Uhr völlig normal, er bemerkt an sich und seinem Raumschiff keine Veränderung. Doch im Endeffekt bedeutet das, wenn er nur ein Jahr lang mit 99,999999% der Lichtgeschwindigkeit unterwegs ist und zur Erde zurück kehrt, sind wir bereits nur noch Staub und Asche, denn es sind über 7000 Jahre seit Beginn seiner Reise vergangen! Wieso aber heben sich beide Effekte nicht gegenseitig auf? Der Astronaut war vor seinem Start im selben, ruhenden Bezugssystem wie wir. Während nun unsere Zeit normal verläuft, verlangsamt sich sein Zeitfluss durch seinen Weltraumflug. Wenn er wieder in unser ruhendes Bezugssystem eintritt, ist ein großer Teil seiner Reisezeit gedehnt worden, nach obigem Beispiel dauerte eine seiner Bordsekunden 7000 Erdsekunden. Weil unsere Zeit somit viel schneller verging, findet er uns nur noch im "Methusalem- Outfit" bei seiner Rückkehr vor.

Wir können die Bewegung auch durch Gravitation ersetzen, um denselben Effekt zu erzielen. Dazu lassen wir unseren (armen!) Astronauten in ein Schwarzes Loch steigen und beobachten ihn aus sicherer Entfernung. Je näher er dem Ereignishorizont kommt, umso langsamer sehen wir seine Uhr gehen. Berührt er den Ereignishorizont, so wird die letzte Sekunde, bevor er in das Loch fällt, unendlich gedehnt. Wir müssten also unendlich lange warten, um ihn darin verschwinden zu sehen. Schonen wir lieber den armen Astronauten und verwenden unsere Zeit sinnvoller!

Zeit ist Privatsache

Wir sehen also, dass die Zeit in verschiedenen Bezugssystemen eine völlig andere Rolle spielen kann, wenn diese sich zueinander bewegen oder von unterschiedlichen Gravitationsfeldern beeinflusst werden. Aber gibt es denn nicht eine für alle Objekte im Kosmos gültige Zeit? Nein, es gibt keine absolute Zeit wie sie vormals von Newton definiert wurde. Es ist nirgendwo im All eine große Uhr aufgehängt, deren Zeit für alle Lebewesen und für jeden beliebigen Ort maßgebend ist. Zeit ist eine reine Privatangelegenheit, denn alle Bezugssysteme unterscheiden sich voneinander. Der Mann, der mit seinem Auto auf der Autobahn fährt, hat eine andere Zeit als seine Frau zu Hause in der Küche. Die Uhr des Reisenden im Zug geht anders als die eines am Bahnhof wartenden Passanten.

Dennoch gibt es so etwas wie eine Kosmische Zeit. Diese begann ja mit dem Urknall und kann vermutlich unendlich lang weiterführen. Es ist die Zeit unseres Universums, und wir erleben wahrscheinlich gerade seine "Kindheit", denn es ist "erst" etwa 13,8 Milliarden Jahre alt.

Das GPS- System

Eine aktuelle Anwendung der Relativitätstheorie findet man im GPS- Satelliten- Navigationssystem (Global Positioning System). Hierzu befinden sich mindestens 24 Satelliten in 20 000 [km] Höhe über der Erde und senden Signale herunter (manchmal sind bis zu 31 im Orbit). Unser Empfänger kennt die Laufzeit des Signals und kann daraus die Position ableiten. Nun geht aber die Uhr des Empfängers langsamer als die der Satelliten, weil sie einer stärkeren Erdanziehung ausgesetzt ist. Diesen relativistischen Effekt muss der Empfänger korrigieren. Verrechnet er sich nur um eine Millionstel Sekunde, so ergibt sich bei einer Ausbreitungsgeschwindigkeit der Funksignale von rund 300 000 [km/s] bereits ein Fehler von 300 [m]!

Der Empfänger muss aber noch mehr wissen:

Die Satelliten umkreisen die Erde nicht auf exakten Kreisbahnen und "spüren" daher unterschiedliche Stärken des Gravitationsfeldes. Das beeinflusst ihre Uhren unterschiedlich. Der Raum um die Erde wird von ihrem Gravitationsfeld gekrümmt, das verändert den Weg der Signale. Und zum Schluss drehen sich Satellit und Empfänger relativ zueinander wegen der Erdrotation.

Würde man alle diese Effekte nicht berücksichtigen, so käme am Ende eine Abweichung von mehreren Kilometern zustande! Zum Glück kann man sie aber berechnen und kann sich über die hohe Genauigkeit des GPS- Systems freuen.

Weitere Informationen zum GPS- System:
https://de.wikipedia.org/wiki/Global_Positioning_System