Schwarze Löcher

Karussell der Raumzeit

Bis jetzt haben wir Schwarze Löcher als einfache, simple Gebilde kennen gelernt, was sie im Grunde auch sind. Man kann sie recht kurz beschreiben durch ihre Masse und dem daraus folgenden Radius. Eine Lösung der Einsteinschen Feldgleichung ("Reissner-Nordström-Lösung") weist darauf hin, dass Schwarze Löcher eine elektrische Ladung besitzen können, was ein weiterer Aspekt ihrer Beschreibung wäre. Es spricht nichts dagegen, dass aus dem Loch elektrische Feldlinien herausragen. Wären sie positiv geladen, würden z.B. Elektronen angezogen, bei negativer Ladung Protonen. Diese Teilchen würden bei ihrem Sturz ins Loch dessen Ladung recht schnell neutralisieren. Das aus dem Grund, weil Schwarze Löcher im Kosmos stets von Materie umgeben sind. Materie besteht aus Elektronen und Protonen (sowie Neutronen), also positiven und negativen Ladungen. Die elektrostatischen Anziehungskräfte eines geladenen Schwarzen Lochs sind eine Milliarde Milliarden Mal stärker als seine Gravitation, daher wäre seine Ladung in kürzester Zeit durch Anziehung der entgegengesetzt geladenen Teilchen neutralisiert. Eine weitere Betrachtung geladener Löcher erübrigt sich daher, denn in der Natur werden wir sie kaum antreffen.

Etwas sehr Wichtiges wurde bei den bisherigen Betrachtungen allerdings noch nicht beachtet: Alle Sterne, die wir beobachten können, rotieren! Bis jetzt führte unsere Reise lediglich zu "statischen" Schwarzen Löchern, also solchen, die nicht rotieren. Doch wenn ein Stern kollabiert, dann muss nach dem physikalischen Gesetz der Drehimpuls erhalten bleiben, es sei denn, er wird durch eine äußere Kraft gebremst. Weil es keine "Bremse" bei einem solchen Ereignis gibt, werden somit die allermeisten Schwarzen Löcher rotieren!

Damit haben wir alles beisammen, um ein Schwarzes Loch zu beschreiben:

Masse Drehimpuls Ladung

Mehr als das kann man niemals über ein Schwarzes Loch erfahren. Man kann hinfliegen und diese Größen messen, aber man wird nie herausbekommen, ob das Loch z.B. aus einem Stern entstanden ist oder vielleicht sogar aus Antimaterie besteht. Nun wird man sich fragen, was passiert denn mit dem Magnetfeld des Sterns, wenn er kollabiert? Es müsste doch zu ungeheurer Stärke verdichtet werden, noch viel mächtiger als bei den Magnetaren. Doch auch hier siegt die Gravitation. Die magnetischen Feldlinien werden immer mehr nach unten gebogen und wenn der Stern den kritischen Radius erreicht hat, ragt keine einzige mehr aus dem Loch heraus. Die Gravitation lässt es nicht zu, dass wir mehr als die drei oben genannten Größen erfahren! Diese Eigenschaften, die ein Schwarzes Loch zu einem "simplen" Gebilde machen, beschrieb 1971 John Wheeler mit dem prägnanten und durchaus zweideutigen Satz

Schwarze Löcher haben keine Haare!

Mit den Haaren ist natürlich all das gemeint, was aus dem Schwarzen Loch, dem Horizont, herausragen könnte. Mit seinem Satz erregte John Wheeler verständlicherweise einige Unruhe unter seinen Wissenschaftskollegen, doch bald legte sich die Aufregung über diese "Obszönität". Heute findet dieser Ausspruch in jeder Abhandlung über Schwarze Löcher seinen selbstverständlichen Platz.

Gegenstände wie Sterne, Hühner oder Autos sind komplizierte Gebilde. Um jedes noch so kleine Detail, bis in den atomaren Aufbau, beschreiben zu können, würde man viele Milliarden von Parametern benötigen. Ein Schwarzes Loch dagegen reduziert alles auf die drei genannten Größen. Es "vergisst" praktisch alles, woraus es entstanden ist und wie der ursprüngliche Aufbau beschaffen war. Masse, Drehimpuls und elektrische Ladung sind alles, was von Sternen, Hühnern oder Autos übrig bleibt, fallen sie in ein Schwarzes Loch. Schwarze Löcher sind die effektivsten Informationsvernichter im Universum (was der aktuellen Meinung von Stephen Hawking allerdings widerspricht, hierzu später aber mehr)!

Doch zurück zu Schwarzen Löchern, die rotieren.

Die Einsteingleichungen für rotierende, nicht geladene Schwarze Löcher sind vom neuseeländischen Mathematiker Roy Kerr erst 1963 gelöst worden, und man nennt solche Objekte nach ihm Kerrsche Löcher. Zunächst beschrieb seine Lösung die Krümmungen der Raumzeit um einen rotierenden Stern. Doch schon bald konnten Brandon Carter, Roger Penrose sowie R.Boyer und R. Lindquist nachweisen, dass Kerrs Lösung alle rotierenden Schwarzen Löcher umfasste. Und was ist an diesen Objekten nun anders als bei den Schwarzschild- Löchern?

Kerrsche Löcher rotieren nicht nur selbst, sondern zwingen allem in ihrer Umgebung diese Rotation auf! Alles, was sich in der Nähe des Horizonts aufhält. Licht oder andere Strahlung, Materie jeder Form und sogar die Raumzeit werden gezwungen, der Rotation des Lochs mit derselben Geschwindigkeit zu folgen. Man kann sich diesen Effekt (genannt frame- dragging) wie einen Strudel vorstellen. Das Mitreißen der Raumzeitgeometrie gilt im Prinzip für jeden rotierenden Körper (und wird dann nach ihren Entdeckern Lense-Thirring-Effekt genannt), ist aber verschwindend gering, solange der Körper nicht zum Schwarzen Loch kollabiert ist.

Wenn Sie einmal den Stöpsel aus der Badewanne ziehen, sehen Sie, dass entfernt vom Abfluss die Wasseroberfläche (die "Raumzeit") noch relativ ruhig ist. Je näher man an den Abfluss herangeht, umso schneller und so wirbelnder werden die Bewegungen. Ähnlich auch beim Schwarzen Loch, direkt an der Oberfläche des Horizonts muss alles mit der Geschwindigkeit des Lochs rotieren. Hier zunächst in einem so genannten Einbettungs- Diagramm die umgebende Raumzeit eines nicht rotierenden Schwarzen Lochs, die Rotation entspricht a = 0. a ist der so genannte Kerr- Parameter, mit dem die Rotation Schwarzer Löcher bezeichnet wird. Er kann Werte zwischen 0 und +1 oder -1 annehmen. Der rote Kreis zeigt jeweils den Ereignishorizont.

Bei einem mit maximaler Geschwindigkeit (a = 1) rotierenden Loch wird die umgebende Raumzeit in einer strudelartigen Form mitgerissen. Ein anderer anschaulicher Vergleich ist etwa ein Tornado, der einen ähnlichen Wirbel erzeugt. Wieso gibt es eigentlich eine maximale Rotationsgeschwindigkeit? Theoretisch könnte man doch einfach mit Drehimpuls behaftete Materie in das Loch werfen, um seine Rotation immer schneller werden zu lassen (der Drehimpuls muss ja erhalten bleiben). Da aber macht uns die Natur einen Strich durch die Rechnung.

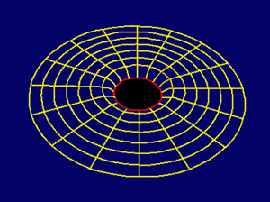
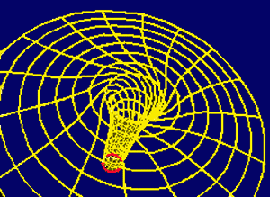
Wenn Sie ihren Kaffee einmal extrem schnell umrühren, so wird ab einer bestimmten Drehzahl durch die Zentrifugalkraft das herrliche Getränk aus der Tasse spritzen, der Zusammenhalt der Flüssigkeit zerreißt. Auch Sterne können nicht mit jeder beliebigen Geschwindigkeit rotieren, denn sonst würden sie durch die Zentrifugalkräfte zerrissen. Das gilt auch für Weiße Zwerge, genauso wie für Neutronensterne, die nicht mehr als etwa 1000 Umdrehungen pro Sekunde durchführen können. Gilt das auch für ein Schwarzes Loch?

Durch die Zentrifugalkraft wird der Horizont (exakt ausgedrückt: die Ergosphäre, siehe weiter unten, der eigentliche Ereignishorizont wird nicht verformt) eines Schwarzen Lochs zusammengepresst, abgeplattet wie die Erde durch ihre Rotation. Irgendwann sollte er doch zerreißen, wenn wir immer mehr Materie mit Drehimpuls hineinwerfen? Leider nein. Es gibt für ein rotierendes Schwarzes Loch eine maximale Geschwindigkeit: Wenn es mit halber Lichtgeschwindigkeit rotiert (a = 1, = "Maximal- Kerr"), lassen es die Zentrifugalkräfte nicht mehr zu, dass Materie ins Loch fällt. Sie wird vom Horizont fortgeschleudert. Würde allerdings Maximal-Kerr tatsächlich exakt erreicht werden, könnten die Zentrifugalkräfte die Gravitation aufheben. Wir hätten dann ein Schwarzes Loch ohne Horizont geschaffen, denn der würde jetzt zerplatzen und wir könnten direkt auf die Singularität sehen!

Man kann aber noch so trickreich vorgehen, wir können weder den Horizont zerstören, noch die Rotation beliebig steigern. Roger Penrose hat 1969 eine Hypothese aufgestellt, die so genannte Kosmische Zensur(cosmic censorship). Demnach ist es einem außenstehenden Beobachter zu keiner Zeit und an keinem Ort des Universums möglich, eine nackte Singularität zu erblicken, also eine Singularität ohne Ereignishorizont. Die Natur scheint uns das generell verwehren zu wollen. Jede echte ("intrinsische", ~aus sich selbst heraus) Singularität muss sich nach der Kosmischen Zensur hinter einem Ereignishorizont verbergen, vom Rest des Universums isolieren. Ein Beobachter kann eine Singularität nur erblicken, wenn er sich in das Schwarze Loch begibt. In der "Praxis" ist es also nicht möglich, dass ein Loch mit maximaler Geschwindigkeit rotiert, jedoch können viele Schwarze Löcher dem maximalen Drehimpuls sehr nahe kommen.

Beschäftigen wir uns nun ein wenig mit dem Horizont Kerrscher Löcher, besser gesagt den Horizonten:

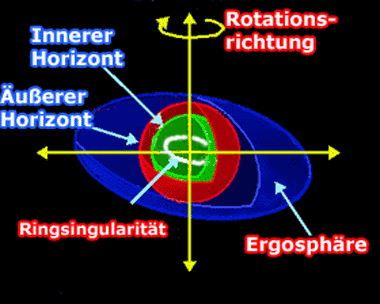
Wie die Skizze schon andeutet, ist der Aufbau stark verändert gegenüber einem nicht rotierenden Loch. Außen umschließt eine so genannte Ergosphäre das Gebilde. Sie hat die abgeplattete Form eines Ellipsoids und stellt ein Gebiet um das Loch dar, in dem keine statisch ruhige Lage mehr möglich ist. Allem, was sich hier aufhält, Materie oder Strahlung, wird die Rotation des Schwarzen Lochs aufgezwungen (frame dragging). Die äußere Begrenzung der Ergosphäre wird deshalb auch statische Grenze genannt. Selbst wenn ein Körper Lichtgeschwindigkeit erreicht, kann er innerhalb der Ergosphäre keine statische Lage mehr einnehmen. Nicht eingezeichnet ist der Übersichtlichkeit halber hier die schon bekannte Photonensphäre, ein Bereich, in dem ein unter günstigem Winkel hinein gelenktes Photon gerade noch auf einer stabilen Bahn umlaufen kann, ohne in das Loch zu fallen.

Weder die Ergosphäre, Photonensphäre noch die statische Grenze stellen einen Ereignishorizont dar. Erst bei weiterem Eintauchen in das Kerr- Loch stoßen wir auf - zwei - Horizonte! Der äußere Horizont befindet sich vollständig innerhalb der statischen Grenze, an den Polen können Ergosphäre und äußerer Horizont sich überschneiden (bei a = 1). Dieser Horizont ist die eigentliche Grenze des Lochs, aus der keine Informationen mehr entweichen können. Darunter befindet sich ein zweiter Horizont, über dessen Bedeutung man sich noch nicht im Klaren ist. Noch weiter innen stoßen wir nun auf eine ringförmig aufgeblasene, jedoch unendlich dünne Singularität in der äquatorialen Ebene. Bei Maximal-Kerr liegt sie, wie dann auch der innere auf dem äußeren Horizont. Wird a = 0, haben wir es wieder mit einem Schwarzschild- Loch zu tun - die Singularität schrumpft zu einer Punktsingularität zusammen.

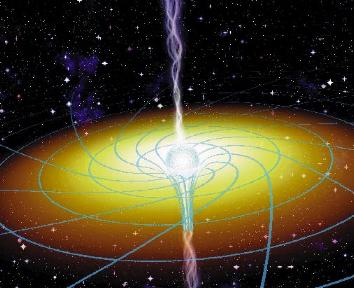
Hier eine weitere Darstellung, wie ein Kerr- Loch die Raumzeit und alles andere mit sich reißt (frame- dragging) und seine Rotation aufzwingt. Vielfach wird gesagt, dass durch die Ringsingularität völlig neue Möglichkeiten eröffnet werden: Man könnte sich oberhalb der Ringebene aufhalten oder sogar durch den Ring hindurch fliegen, zumindest bei supermassereichen Löchern, da hier die Gezeitenkräfte noch erträglich wären. Der Ring stelle nicht das Ende der Raumzeit dar, wie es bei einer intrinsischen Punktsingularität der Fall ist. Prinzipiell könnten wir unseren Astronauten also wieder auf die Reise schicken, und nach manchen Vermutungen sollte er durch die Ringsingularität sogar andere Universen erreichen. Allerdings liegen solche Spekulationen jenseits jeder Realität, niemand kann den Sturz in ein Schwarzes Loch überleben! Zunächst einmal dürfte es keine Konstruktion und keinen Organismus geben, die den Belastungen der Rotation mit evtl. relativistischen Geschwindigkeiten schon in Horizontnähe widerstehen könnten. Direkt am Horizont hätte jeder Gegenstand Lichtgeschwindigkeit, um dann überlichtschnell weiter zu stürzen! Materie in der uns bekannten Form kann hier wohl nicht mehr existieren, weil die Geodäten der Teilchen raumartig werden. Das bedeutet, dass die Teilchen tachyonische Eigenschaften annehmen, sich außerhalb aller von uns fassbaren Grenzen bewegen. Deshalb bleibt fortan unser Astronaut von allen Blessuren verschont.

Mit freundlicher Genehmigung von J. Bergeron/Sky & Telescope

Damit kennen wir jetzt alle Arten von Schwarzen Löchern, die denkbar sind:

Das Schwarzschild- Loch. Es ist statisch, rotiert also nicht und ist kugelsymmetrisch. Für seine Beschreibung genügt die Masse
Das Schwarze Loch nach Reissner-Nordström: Es rotiert auch nicht, ist ebenfalls kugelsymmetrisch, aber elektrisch geladen
Das Kerrsche Loch. Zu seiner Beschreibung braucht man Masse und Drehimpuls
Die wahrscheinlichste Lösung eines Gravitationskollapses: Ein im Gleichgewicht befindliches, rotierendes Loch mit einer geladenen Masse. Es wird Kerr-Newman- Loch genannt.

Für die Masse eines Schwarzen Lochs ist keine Begrenzung bekannt, sie kann beliebige (!) Größen annehmen. Das gilt jedoch nicht für die Ladung und den Drehimpuls, ihnen ist ein oberes Limit gesetzt. Würde es überschritten, z.B. beim Kollaps eines Sterns, so könnte kein Schwarzes Loch entstehen, sondern eine nackte Singularität. Das aber verbietet die Kosmische Zensur!

Jetzt wollen wir uns ansehen was passiert, wenn Materie zu engen Kontakt mit Schwarzen Löchern hat.

Weitere Informationen: http://www.wissenschaft-online.de/astrowissen/lexdt_k02.html#kerr