Die Keplerschen Gesetze

Bereits im Jahre 1609 formulierte Johannes Kepler (1571 bis 1630, linkes Bild) die ersten zwei seiner Gesetze in seiner Astronomia Nova.

Er konnte sie ableiten aus dem ausgezeichneten Beobachtungsmaterial des dänischen Astronomen Tycho Brahe (1546 bis 1601, rechtes Bild), dessen Mitarbeiter Kepler von 1600 bis zum Tod Tychos war. Das erste Gesetz lautet:

Die Planeten bewegen sich auf Ellipsen, in deren einem Brennpunkt die Sonne steht.

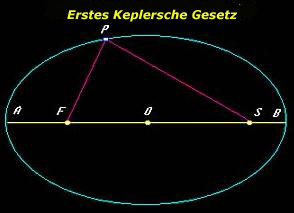
Das Verhältnis OS/OB ergibt die Exzentrizität.

Wie wir heute wissen, sind diese (Kepler-) Ellipsen allerdings nicht geschlossen, sondern weisen aufgrund relativistischer Effekte Abweichungen auf. Es bildet sich eine so genannte Rosettenbahn, welche besonders gut bei Merkur als Periheldrehung zu beobachten ist. Darunter versteht man die Drehung der Apsidenlinie (Verbindungslinie sonnenfernster- und nächster Punkt) der Planetenbahn innerhalb der Bahnebene. Diese Abweichung wurde bereits von der Relativitätstheorie vorhergesagt.

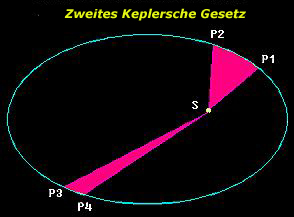
Das zweite Gesetz (der Flächensatz) besagt:

Die von der Sonne zu einem Planeten gezogene Linie, der Fahrstrahl, (oder heute besser als Radiusvektor Sonne- Planet bezeichnet), überstreicht in gleichen Zeiten gleiche Flächen.

Im dritten Gesetz, welches 1618 erschien, bringt Kepler die Umlaufzeiten und großen Halbachsen der Planetenbahnen in eine Beziehung:

Die Quadrate der Planetenumlaufzeiten verhalten sich wie die dritten Potenzen der großen Halbachsen ihrer Bahnellipsen:

(T₁/T₂)² = (a₁/a₂)³

Durch eine Ergänzung hat das Gesetz auch heute noch in gewissem Umfang Gültigkeit:

(T₁/T₂)² = (a₁/a₂)³ (M+m₂) / (M+m₁)

Hierin bedeuten:

• T₁,T₂: Umlaufzeit Planet 1,2
• a₁,a₂: große Halbachse Planet 1,2
• M: Masse Sonne
• m₁,m₂: Masse Planet 1,2

Es bestehen allerdings noch geringe Abweichungen aufgrund der Gravitationswirkung der großen Planeten.