Die Helligkeit der Sterne
Wenn wir in einer klaren Nacht die Sterne betrachten, so erscheinen sie uns unterschiedlich hell. Sirius z.B. ist sehr leicht als wesentlich heller zu erkennen als die Gürtelsterne des Orion. Dieses visuelle Empfinden bezeichnet man als scheinbare oder visuelle Helligkeit, Formelzeichen ist allgemein das oder (abgeleitet von magnitudo, lat., Größe).
Bereits in der griechischen Antike wurden durch HipparchosHipparchos von Nicäa, 190 v. Chr. - 120 v. Chr., der bedeutendste griechische Astronom seiner Zeit, gilt als Begründer der wissenschaftlichen Astronomie die mit bloßem Auge sichtbaren Sterne in 6 Größenklassen eingeteilt, wobei ein Stern sechster Größe gerade noch sichtbar ist, die hellsten dagegen haben die Helligkeit . So ordnen sich die 15 hellsten Sterne der ersten Größe zu, bis zu finden sich etwa 150 und bis zu etwa 5000 Sterne, die gerade noch mit bloßem Auge sichtbar sind. Die Bezeichnung magnitudo wird dabei häufig als als Hochzahl geschrieben, z.B. . Weil diese Skala aber bei vielen Sternen nur unzureichend war, setzten Astronomen um das Jahr 1800 für noch hellere Objekte ein Minuszeichen vor die Größe und erweiterten die Helligkeitsklassen zur feineren Unterscheidung durch weitere Dezimalstellen. So haben sich folgende Schreibweisen eingebürgert: , , oder
Demnach hat dann Sirius eine scheinbare Helligkeit von -1,47m und die Sonne leuchtet mit - 26,7m (oder als andere Schreibweise -26m7). Ein Stern erster Größe ist um den Faktor 100 heller als einer mit 6m (siehe Rechenbeispiel unten), und von einer Klasse zur anderen liegt ein Helligkeitssprung um den Faktor 2,5. Die Helligkeitsskala ist logarithmisch aufgebaut und definiert die Energie des einfallenden Lichts als Strahlungsstrom . Wenn die Magnituden zweier Sterne sind, so gilt:
Daraus ergibt sich, dass z.B. die Klasse 3m um den Faktor 2,512 heller ist als ein Stern der Größe 4m, entsprechend einem Logarithmus von 0,4.
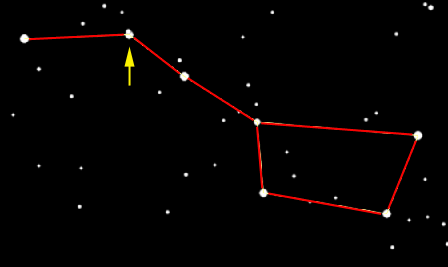
Ein bekannter Prüfstein für das bloße Auge ist der Stern Alkor, auch genannt Das Reiterlein im Sternbild Großer Wagen (Ursa major). Alkor ist Begleiter des mittleren Deichselsterns Mizar und hat die visuelle Größe 4m0. Wer ihn sehen kann hat nicht nur gute Augen, sondern auch brauchbare Sichtverhältnisse.
Mit einem Fernrohr von 100 [mm] Öffnung kann man noch Sterne von 11m7 erkennen, bei 500 [mm] sind es 14m5. Mount Palomar dagegen sieht noch Objekte von 23m, das Keck- Teleskop bis zu 27m. Natürlich schätzen die Astronomen die Sternhelligkeit nicht mit bloßem Auge ab, sondern sie wird fotometrisch ermittelt. Die fotometrische Helligkeit ist dabei von der rein visuellen durch andere spektrale Empfindlichkeit etwas abweichend. Als Referenzstern dient Wega, der die Größe 0m zugeordnet wird, zur Eichung fotometrischer Messgeräte eine Gruppe von Sternen nahe dem Himmelsnordpol, der so genannten Polsequenz.
Die scheinbare Helligkeit sagt aber nichts über die wirkliche Strahlungsintensität eines Sterns aus, denn die ist von seiner Entfernung abhängig. So kann eine sehr starke Strahlungsquelle (z.B. ein Quasar) doch nur sehr schwach erscheinen aufgrund einer großen Distanz, während eine schwache Lichtquelle wie die Venus sehr hell ist, weil sie uns nahe steht. Hinzu kommt, dass das Licht der Sterne auf dem Weg zu uns durch die Interstellare Materie abgeschwächt wird, wir sprechen hier von der so genannten Extinktion (= Lichtdurchlässigkeit). Man benötigt also eine Angabe über die absolute Helligkeit , die man willkürlich festgelegt hat: Objekte außerhalb des Sonnensystems erscheinen dann mit einer Helligkeit, mit welcher sie aus einer Entfernung von 10 Parsec (32,6 [LJ]) strahlen würden. Für Körper des Sonnensystems hat man dazu eine Distanz von einer Astronomischen Einheit festgelegt.
Leicht kann man diese absolute Helligkeit berechnen, wenn man die Entfernung des Probanden kennt. Dazu dient die einfache Formel
wobei die Entfernung in Parsec ist. Berechnet man hiernach die absolute Helligkeit der Sonne, so erscheint sie nur noch als schwacher Stern von M = 4,8. Für Deneb im Schwan, der eine scheinbare Helligkeit von 1,25m hat und 500 [pc] entfernt ist, erhält man dann M = - 7,2, womit er fast 65000- mal heller als die Sonne ist. Insgesamt erstrecken sich die absoluten Helligkeiten über 30 (!) Klassen, was bedeutet, dass Sterne 1 Million mal so hell wie die Sonne sein können, aber auch 1 Million mal schwächer.
Wenn ein Astronom auf der Erde nun die Helligkeit eines Sterns bestimmt, so erfasst er nur einen bestimmten Teil des Strahlungsspektrums. Ein bedeutender Teil der Strahlungsleistung des Sterns wird von der Erdatmosphäre verschluckt, weil sie für unterschiedliche Wellenlängen verschieden durchlässig ist. Will man die Helligkeit aber über das ganze Spektrum des Sterns wissen, so benötigt man die bolometrische Helligkeit. Sie ist allerdings nicht leicht zu bestimmen, weil die Messgeräte immer nur einen bestimmten Teil des Spektrums erfassen. Hat man jedoch Kenntnis über die Energieverteilung im Sternspektrum, so kann man durch bolometrische Korrekturfaktoren aus der scheinbaren die bolometrische Helligkeit ableiten. Zwischen der Strahlungsleistung (Leuchtkraft) eines Sterns und der bolometrischen Helligkeit besteht folgender Zusammenhang:
wobei in Einheiten der Sonnenleuchtkraft (3,85 x 1026 [W]) angegeben wird. Ein Stern der bolometrischen Helligkeit Mbol = 0m hat eine Leuchtkraft von 3,03 x 1025 [W].
Nun soll noch gezeigt werden, wie man den Helligkeitsunterschied zwischen zwei Himmelskörpern berechnen kann. Betrachten wir dazu als erstes Beispiel Sonne und Mond:
Sei das hellere Objekt, das dunklere, so ist der gesuchte Unterschied in Größenklassen :
Der Helligkeitsunterschied ergibt sich zu
Die Sonne hat die visuelle Helligkeit -26m73, der Vollmond -12m6. Wir rechnen:
Die Sonne ist demnach 449 000 Mal heller als der Vollmond.
Ein anderes Beispiel:
Wie viel heller ist die Venus (-4m7) als der hellste Stern Sirius (-1m47)?
Die Venus erscheint uns also fast 20 Mal heller als Sirius.
Abschließend noch eine tabellarische Übersicht der visuellen Helligkeiten einiger bekannter Objekte:
| Magnitude vis. m | Objekt |
|---|---|
| -26.73 | Sonne (449 000 Mal heller als der Vollmond) |
| -20 | Sonne, von Neptun aus gesehen |
| -12.6 | Vollmond |
| -6.0 | Supernova SN 1054 im Krabbennebel, 6500 Lichtjahre entfernt |
| -4.7 | Größte Helligkeit der Venus und der ISS |
| -3.0 | Größte Helligkeit des Mars |
| -2.8 | Größte Helligkeit von Jupiter |
| -1.47 | Der hellste Stern: Sirius |
| -0.72 | Canopus |
| -0.24 | Größte Helligkeit von Saturn |
| -0.04 | Arcturus |
| -0.01 | α Centauri A |
| 0 | Der "Nullpunkt": Wega |
| 0.112 | Rigel |
| 1.09 | Antares |
| 2.01 | Polaris |
| 5.1 | Größte Helligkeit des Asteroiden Vesta |
| 5.5 | Größte Helligkeit von Uranus |
| 6.5 | Schwächster noch mit bloßem Auge unter perfekten Bedingungen sichtbarer Stern |
| 7.7 | Größte Helligkeit von Neptun |
| 12.9 | Hellster Quasar 3C 273 in 2.4 Gigalichtjahren Distanz |
| 13.65 | Größte Helligkeit von Pluto |
| 18.7 | Derzeitige Helligkeit des Zwergplaneten Eris |
| 23 | Größte Helligkeit von Plutos Monden Hydra und Nix |
| 27 | Schwächste Objekte mit 8m- Keck- Teleskop |
| 30 | Schwächstes Objekt im Hubble Weltraumteleskop |
| 35 | Sedna im Aphel |