Physikalischer Hintergrund von Raumzeit- Reisen in Science Fiction
Inhaltsverzeichnis:
1. Einleitung
2. Physikalische Grundlagen
2.1 Die Spezielle Relativitätstheorie
2.2 Die Allgemeine Relativitätstheorie
2.3 Antimaterie
3. Analyse von Raumzeit-Reisen der Science Fiction
3.1 Reisen durch den Raum
3.1.1 Unterlichtschnelle Bewegung per Impulsantrieb
3.1.2 Überlichtschnelle Bewegung
3.1.2.1. Warpantrieb
3.1.2.2. Wurmlöcher
3.2 Reisen durch die Zeit
3.2.1 Reisen mittels Zeitdilatation
3.2.2 Reisen mittels Wurmlöcher
3.2.3 Paradoxien
4. Schlussbewertung
5. Quellenverzeichnis
6. Anhang
6.1 Anhang I
6.2 Anhang II
6.3 Anhang III
6.4 Anhang IV
6.5 Anhang V
6.6 Anhang VI
6.7 Anhang VII
6.8 Anhang VIII
6.9 Anhang IX
6.10 Anhang X
6.11 Anhang XI
6.12 Anhang XII
1. Einleitung
- Lawrence M. Krauss, Professor für Physik und Astronomie -
"Was geschehen kann, wird auch geschehen"2
- Data, Androide -
Diese Aussage hat sich in der Geschichte der Physik schon oft bestätigt. Als der deut-sche Astronom Karl Schwarzschild 1916 eine Lösung der Gleichungen der Allgemeinen Relativitätstheorie angab, deuteten seine Ergebnisse auf die Existenz von Schwarzen Lö-chern hin, die damals jedoch noch "gravitativ vollständig kollabiertes Objekt"3 genannt wurden. Albert Einstein verwahrte sich jedoch lange Zeit gegen solche Objekte, weil ihm die darin enthaltene Singularität "physikalisch unrealistisch"4 erschien. Heute sind Schwarze Löcher allgemein anerkannt, denn es wurden zahlreiche Phänomene nachgewie-sen, die auf ihre Existenz hindeuten. Genau wie im Fall Schwarzer Löcher erscheinen heute hypothetische Konstrukte wie Wurmlöcher oder Zeitreisen vielen Wissenschaftlern als unphysikalisch und der amerika-nische Physiker Kip Thorne gibt zu, dass man in diesen Fällen häufig Angst hat, sich vor den "Kollegen lächerlich zu machen, wenn unsere Forschungsarbeit in diese Richtung geht"5 , da es dann zu sehr nach Science Fiction klingt.
In den letzten Jahren hat sich diese strikte Trennung zwischen Science und Fiction je-doch merklich aufgelöst und Wissenschaftler befassen sich zunehmend ernsthaft mit Ideen der Science Fiction. Das wird auch dadurch deutlich, dass viele anerkannte Physiker wie der Brite Stephen W. Hawking von der Cambridge University, begeisterte Science Fiction Leser sind und einige, so zum Beispiel Gregory Benford, sogar selbst solche Literatur ver-fassen. So denken Physiker heute zum Beispiel darüber nach, ob nicht doch Schlupflöcher in Einsteins Relativitätstheorie bestehen, die Reisen schneller als das Licht zulassen. Auch Wurmlöcher oder Zeitreisen sind Bestandteile der Forschungsarbeit von Physikern. Scien-ce Fiction und Wissenschaft ergänzen sich also gegenseitig, was Hawking folgendermaßen erklärt: "Die von der Science Fiction präsentierten Ideen gehen ab und zu in wissenschaft-liche Theorien ein. Und manchmal bringt die Wissenschaft Konzepte hervor, die noch selt-samer sind als die exotischste Science Fiction."6 Einige für Science Fiction Literatur typische Themen werden neuerdings auch physikalisch untersucht. Sie sollen in dieser Facharbeit näher betrachtet werden, wobei zunächst grundlegende physikalische Fakten erklärt werden und im zweiten Teil der Bezug zur Science Fiction hergestellt wird.
2Krauss, Lawrence M.: Die Physik von Star Trek. Wolfgang Jeschke. 6. Auflage. - München:(Wilhelm Heyne Verlag GmbH & Co. KG); S. 28
3Vaas, Rüdiger: Tunnel durch Raum und Zeit. - Stuttgart:(Franckh-Kosmos Verlags-GmbH & Co. KG) 2005; S. 23
4Vaas, Rüdiger: Tunnel durch Raum und Zeit. - Stuttgart:(Franckh-Kosmos Verlags-GmbH & Co. KG) 2005; S. 35
5Thorne, Kip: Gekrümmter Raum und verbogene Zeit. Lewis Thomas. Bd. 9 der Reihe: The Commonwealth Fund Book Program. - München:(Droemer Knaur) 1994; S. 563
6Krauss, Lawrence M.: Die Physik von Star Trek. Wolfgang Jeschke. 6. Auflage. - München:(Wilhelm Heyne Verlag GmbH & Co. KG); S. 9
2. Physikalische Grundlagen
2.1. Die Spezielle Relativitätstheorie
Im Jahr 1905 veröffentlichte Albert Einstein eine maßgebende, neue physikalische Theorie, die heute als Spezielle Relativitätstheorie bekannt ist. Im Folgenden wird erst ein kurzer Überblick über das physikalische Wissen um die Jahrhundertwende gegeben und daraufhin werden die wichtigsten Aussagen der Speziellen Relativitätstheorie erklärt.
Ende des 19. Jahrhunderts wähnten sich viele Wissenschaftler im Glauben, die Welt vollständig zu verstehen, und meinten, alle wesentlichen Dinge des Kosmos erklären und berechnen zu können. Möglich war dies durch ein Gedankengebäude, das auf der Newton-schen Physik beruhte, also vor allem auf den Bewegungs- und Gravitationsgesetzen sowie auf der Vorstellung von absolutem Raum und absoluter Zeit. Im Rahmen der bekannten physikalischen Theorien konnte man eine Vielzahl experimenteller Befunde erklären, insbesondere im Bereich der Astronomie und des Elektromagnetismus. Die technische Ent-wicklung erlaubte immer genauere Messmethoden. So maßen die amerikanischen Experimentalphysiker Albert A. Michelson und Edward W. Morley in den Jahren 1881-87 die Lichtgeschwindigkeit mit einer neuen, auf Interferenzeffekten beruhenden Methode7 . Ihr Ergebnis widersprach den allgemeinen Erwartungen, die besagten, dass die Geschwindigkeit des Lichts eines anderen Himmelskörpers kleiner ist, wenn sich die Erde von diesem Himmelskörper weg bewegt, und dass die Geschwindigkeit des Lichts größer ist, wenn sich Erde und Himmelskörper aufeinander zu bewegen. Im Gegensatz zur Newtonschen Vorstellung, nach der sich zwei Geschwindigkeitsvektoren relativ zu einer alles durchdringenden Substanz namens Äther, die als hypothetisches Trägermedium für elektromagnetische Wellen vermutet wurde, addieren, wenn sie in die selbe Richtung gerichtet sind, und sich relativ zu dem Äther subtrahieren, wenn sie entgegengesetzt gerichtet sind, maßen Michelson und Morley eine stets konstante Geschwindigkeit des Lichts, egal wie der Bewegungszustand des Senders oder des Empfängers durch den Äther ist.
Auch ein anderer Befund ließ Risse im Fundament der Newtonschen Physik erkennen. So sagt eine der vier Maxwell- Gleichungen aus, dass unter der Annahme eines absoluten Raumes magnetische Feldlinien einem bewegten Beobachter unterbrochen erscheinen können. Solche Tatsachen erschienen einigen Physikern "hässlich und unbefriedigend"8 . Es gab Versuche, das Michelson- Morley-Experiment zu erklären und die Maxwell- Gleichungen in eine einfache Form ohne abgeschnittene Feldlinien zu bringen. Dazu musste man sich jedoch vom absoluten Raum und der absoluten Zeit trennen und zusätzlich eine bis dahin geheimnisvolle Längenkontraktion und Zeitdilatation relativ zum Äther bewegter Objekte annehmen. Diese erschienen dem Großteil der Physiker jedoch abwegig, da man versuchte, alles durch Kräfte zu erklären, die hier nicht nachweisbar waren. So ignorierten viele Wissenschaftler einfach die unerklärlichen Befunde, war die Newtonsche Physik doch immer so erfolgreich gewesen.
Albert Einstein, ein bis dahin noch unbekannter junger Physiker, nahm diese Ideen 1905 wieder auf und führte sie konsequent weiter. Dadurch brachte er das Gebäude der Newtonschen Physik völlig zum Einsturz, da er gezwungen war seine Annahmen auf andere, fundamentale Prinzipien zu gründen. Erstens berief er sich auf das Prinzip der Absolutheit der Lichtgeschwindigkeit, die völlig unabhängig vom Bewegungszustand eines Beobachters im Vakuum stets  beträgt. Dadurch ließ sich das Experiment von Michelson und Morley erklären. Die zweite Grundannahme Einsteins war das Prinzip der Relativität. Es sagt aus, dass kein Bezugssystem einem anderen vorgezogen werden darf und somit alle Naturgesetze für alle Bewegungszustände eines Beobachters gleichrangig gelten müssen. Im Rahmen der Speziellen Relativitätstheorie gilt dies jedoch nur für Inertialsysteme, also für gleichförmig geradlinig bewegte Systeme, auf die keine Kräfte von außen einwirken. Einstein verwarf dabei völlig die Vorstellung vom absoluten Raum und der absoluten Zeit. "Und was den Äther betrifft: Er existiert nicht."9
beträgt. Dadurch ließ sich das Experiment von Michelson und Morley erklären. Die zweite Grundannahme Einsteins war das Prinzip der Relativität. Es sagt aus, dass kein Bezugssystem einem anderen vorgezogen werden darf und somit alle Naturgesetze für alle Bewegungszustände eines Beobachters gleichrangig gelten müssen. Im Rahmen der Speziellen Relativitätstheorie gilt dies jedoch nur für Inertialsysteme, also für gleichförmig geradlinig bewegte Systeme, auf die keine Kräfte von außen einwirken. Einstein verwarf dabei völlig die Vorstellung vom absoluten Raum und der absoluten Zeit. "Und was den Äther betrifft: Er existiert nicht."9
Geschwindigkeiten sind immer nur relativ zu anderen Objekten messbar und es ist sinnlos, von einem Zustand der absoluten Ruhe zu sprechen.
Daraus sagte Einstein die sogenannte Zeitdilatation voraus, das heißt eine Dehnung der Zeit. Gemäß der Formel
 ( I )
( I )
verstreicht die Zeit in relativ zu einem Bezugssystem  mit konstanter Geschwindigkeit bewegten Systemen langsamer als in
mit konstanter Geschwindigkeit bewegten Systemen langsamer als in  . Bewegt sich zum Beispiel eine Uhr
. Bewegt sich zum Beispiel eine Uhr  für die Zeitdauer
für die Zeitdauer  in Bezug auf
in Bezug auf  mit konstanter Geschwindigkeit
mit konstanter Geschwindigkeit  , so verstreicht in
, so verstreicht in  die um den Faktor
die um den Faktor  längere Zeitspanne
längere Zeitspanne  . Angenommen
. Angenommen  bewegt sich ab
bewegt sich ab  , also auch ab
, also auch ab  , mit der Geschwindigkeit
, mit der Geschwindigkeit  relativ zu
relativ zu  und beendet die Bewegung bei
und beendet die Bewegung bei  so zeigt eine Uhr, die sich in S auf Höhe von
so zeigt eine Uhr, die sich in S auf Höhe von  befindet, die Zeit
befindet, die Zeit  an. Diese Zeit ergibt sich aus
an. Diese Zeit ergibt sich aus  , wobei
, wobei  das Produkt des Faktors
das Produkt des Faktors  mit
mit  ist.
ist.
Die Zeitdilatation sowie die Längenkontraktion (siehe Anhang I), eine weitere Folge-rung Einsteins, machen sich nur bei relativistischen Geschwindigkeiten bemerkbar, also bei solchen, die größer als 10% der Lichtgeschwindigkeit sind (siehe Anhang II). Dies war auch ein Grund, warum einige Physiker so vehement gegen Einsteins Theorie waren, die erst in den späten 30er Jahren endgültig durch Experimente bestätigt wurde10.
Doch noch zwei weitere wichtige Aussagen macht die Spezielle Relativitätstheorie. Dabei geht es um die Massenzunahme eines Körpers in Abhängigkeit von seiner relativen Geschwindigkeit. So nimmt die Masse  eines Körpers der Ruhemasse
eines Körpers der Ruhemasse  gemäß der Formel
gemäß der Formel
 ( II )
( II )
zu, wenn dieser sich mit der konstanten Geschwindigkeit  in einem Bezugssystem bewegt. Hat zum Beispiel ein Proton der Ruhemasse
in einem Bezugssystem bewegt. Hat zum Beispiel ein Proton der Ruhemasse  relativ zu einem Beobachter
relativ zu einem Beobachter 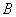 die Geschwindigkeit
die Geschwindigkeit  , so nimmt seine Masse
, so nimmt seine Masse  für
für 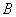 um
um  zu und beträgt
zu und beträgt  Kg, hat sich also etwas mehr als verdreifacht. Doch wie bei Zeitdilatation und Längenkontraktion gilt auch hier, dass der Effekt im täglichen Leben nicht bemerkt werden kann, da
Kg, hat sich also etwas mehr als verdreifacht. Doch wie bei Zeitdilatation und Längenkontraktion gilt auch hier, dass der Effekt im täglichen Leben nicht bemerkt werden kann, da
 bei 'menschlichen' Geschwindigkeiten mit guter Näherung gleich Eins ist und somit die Masse sich nicht merklich ändert.
bei 'menschlichen' Geschwindigkeiten mit guter Näherung gleich Eins ist und somit die Masse sich nicht merklich ändert.
Die zweifellos bekannteste Formel von Einstein lautet
E = m(v)c2 ( III )
und drückt die Äquivalenz von Masse m(v) und Energie E aus, wobei als Umrechnungsfaktor das Quadrat der Lichtgeschwindigkeit dient. Masse ist also eine Form von Energie und kann in sie umgewandelt werden und Energie besitzt Trägheit, wobei vergleichsweise viel Energie in wenig Masse enthalten ist. So enthält beispielsweise Materie der Masse m(v) = 1,00 g die Energie  , eine Energiemenge, mit der man "eine ganze Stadt für mehrere Tage versorgen"11 könnte.
Diese Ergebnisse waren ein Segen für Einstein, denn sie verschafften ihm die Aufmerksamkeit anderer Physiker und bis heute Weltruhm. Für die Science Fiction erwiesen sie sich eher als Fluch, wie später gezeigt wird. Doch zunächst bleiben wir bei Einstein.
, eine Energiemenge, mit der man "eine ganze Stadt für mehrere Tage versorgen"11 könnte.
Diese Ergebnisse waren ein Segen für Einstein, denn sie verschafften ihm die Aufmerksamkeit anderer Physiker und bis heute Weltruhm. Für die Science Fiction erwiesen sie sich eher als Fluch, wie später gezeigt wird. Doch zunächst bleiben wir bei Einstein.
8Thorne, Kip: Gekrümmter Raum und verbogene Zeit. Lewis Thomas. Bd. 9 der Reihe: The Commonwealth Fund Book Program. - München:(Droemer Knaur) 1994; S. 73
9Thorne, Kip: Gekrümmter Raum und verbogene Zeit. Lewis Thomas. Bd. 9 der Reihe: The Commonwealth Fund Book Program. - München:(Droemer Knaur) 1994; S. 79
10vgl. Vaas, Rüdiger: Tunnel durch Raum und Zeit. - Stuttgart:(Franckh-Kosmos Verlags-GmbH & Co. KG) 2005; S. 183
11Davies, Paul: So baut man eine Zeitmaschine. Eine Gebrauchsanweisung. - München:(Piper Verlag GmbH); S. 38
2.2. Die Allgemeine Relativitätstheorie
Im Jahr 1907 war Einstein bereits ein angesehener Physiker und wurde deswegen gebeten, einen Übersichtsartikel über die Spezielle Relativitätstheorie zu schreiben. Beim Schreiben dieser Zusammenfassung stieß er auf das Problem, die Gravitation in seine Überlegungen mit einzubeziehen, die in der Speziellen Relativitätstheorie im Sinne eines idealisierten Universums überhaupt nicht vorkommt, da diese sich auf Inertialsysteme beschränkt. Der Schlüssel zur Lösung dieses Problems war ein Gedanke, den Einstein später "als den glücklichsten seines Lebens"12 bezeichnete: "Wenn sich eine Person im freien Fall befindet, dann spürt sie ihr eigenes Gewicht nicht."13 Die Konsequenz daraus ist, dass niemand unterscheiden kann, ob er sich in einem Bezugssystem geringer räumlicher Ausdehnung (= lokales Bezugssystem ) befindet, das selbst, bezogen auf ein äußeres Gravitationsfeld, frei fällt, oder in einem Inertialsystem fern von jeder Gravitation. Angenommen eine Person springt mit einem Ball in der Hand aus einem Flugzeug und lässt den Ball im freien Fall los. Denkt man sich den Luftwiderstand weg, dann kann die Person mit geschlossenen Augen nicht entscheiden, ob sie und der Ball im freien Fall sind oder mitten im All ohne Gravitation, denn in beiden Fällen bewegt sich der Ball nicht aus der Hand der Person. Den Sachverhalt, dass alle physikalischen Gesetze sowohl in jedem lokalen, frei fallenden Bezugssystem in einem Universum mit Gravitation als auch in jedem Inertialsystem in einem Universum ohne Gravitation gelten müssen, bezeichnet man als Äquivalenzprinzip. Aus ihm folgt, dass alle Aussagen der Speziellen Relativitätstheorie auch in lokalen, freifallenden Bezugssystemen gelten. Die Bezugssysteme müssen lokal sein, damit der Gezeiteneffekt vernachlässigt werden kann, also die unterschiedlich starke Anziehung der dem gravitationsausübenden Objekt zu- und abgewandten Seite des freifallenden Objektes.
Vom Äquivalenzprinzip gelangte Einstein zu einem weiteren Ergebnis, der gravitativen Zeitdilatation. Sie sagt aus, dass die Zeit für einen Beobachter umso mehr gedehnt ist, je näher das gravitationsausübende Objekt ist. Zeit vergeht also schneller, wenn man sich fern von jeglicher Materie befindet, zum Beispiel im Weltraum, als nahe einer großen Masse. Auf der Erde ist dieser Effekt so gering, dass er nur mit auf Bergen oder in Flugzeugen stationierten Atomuhren gemessen werden kann, jedoch groß genug, um Satelliten regelmäßig synchronisieren zu müssen, damit sie stets die selbe Zeit wie auf der Erdoberfläche haben. Mit diesen Ergebnissen, dem Äquivalenzprinzip und der gravitativen Zeitdilatation, war jedoch noch keine allgemeine Beschreibung der Gravitation aus relativistischer Sicht gegeben. Einstein wandte sich erneut dem Gezeiteneffekt zu, der, wenn man ihn aus Sicht der Newtonschen Physik betrachtet, einen Widerspruch mit dem Relativitätsprinzip aufweist. Gemäß der Speziellen Relativitätstheorie ist der Abstand zweier Objekte (in diesem Fall zweier Himmelskörper) abhängig von den messenden Bezugssystemen. Welche Messung sollte man also als Grundlage für die Berechnung der Anziehungskraft nehmen? Dieses Problem und die gravitative Zeitdilatation versuchte Einstein durch die Annahme zu begründen, "die Zeit sei gekrümmt, der Raum jedoch flach."14
Er hoffte auch andere unerklärliche Phänomene wie zum Beispiel die scheinbar anomale Bewegung des Merkur logisch begründen zu können. Astronomen beobachteten, dass Merkur keine exakt elliptische Bahn um die Sonne beschreibt, sondern eine sogenannte Rosettenbahn15 . Tatsächlich wandert sein sonnennächster Punkt, das Perihel, pro Merkurjahr um 1,38 Bogensekunden weiter um die Sonne (siehe Anhang III). Mit der Newtonschen Physik ließe sich bestenfalls eine Perihelverschiebung "von 1,28 Bogensekunden erklären."16 Doch statt die Differenz von 0,1 Bogensekunden begründen zu können, stieß Einstein wiederum auf einen Widerspruch mit dem Relativitätsprinzip. Um diesen zu beseitigen, musste er auf die Gedanken von Hermann Minkowski zurückgreifen, einem deutschen Mathematiker und Physiker, der 1908 auf vorwiegend ma-thematischem Wege aus der Speziellen Relativitätstheorie folgerte, Raum für sich und Zeit für sich würden "von Stund an [...] völlig zu Schatten herabsinken, und nur noch eine Art Union der beiden soll Selbständigkeit bewahren."17 Mit dieser ,Union' ist die Raumzeit gemeint, welche vierdimensional und absolut ist, also unabhängig vom beobachtenden Bezugssystem gleich. Beobachter in verschiedenen Bezugssystemen nehmen dabei nur "unterschiedliche dreidimensionale Ausschnitte der vierdimensionalen Realität"18 wahr, so wie Menschen mit jeweils einem geschlossenen Auge ein Lineal aus verschiedenen Blickwinkeln unterschiedlich lang erkennen19. Für Einstein, der bis 1912 nie viel von Minkowskis Entdeckung gehalten hat, bedeutete dies, dass, wenn Raum und Zeit untrennbar in einer Raumzeit bestehen, eine Krümmung der Zeit dann auch zwangsläufig eine Krümmung des Raumes ist, also eine Krümmung der Raumzeit. Diese vierdimensionale Krümmung kann sich der Mensch unmöglich vorstellen, man kann aber trotzdem ihr Wesen verstehen, indem man die Analogie zu einer zweidimensionalen Krümmung sucht. Dort erscheint jede Linie, die eine kürzeste Verbindung von zwei Punkten ist, auf hinreichend kleinen Gebieten betrachtet wie eine Gerade und die Krümmung bleibt unbemerkt. Ebenso erscheint jedes Teilchen, das "in freier Bewegung [...] in unserem realen Universum durch ein kleines freifallendes Inertialsystem fliegt"21 als ob es sich entlang einer Geraden durch dieses Bezugssystem bewegt. Da die oben für den zweidimensionalen Raum beschriebene Linie geodätische Linie genannt wird, folgerte Einstein, dass sich freifallende Teilchen in der vierdimensionalen Raumzeit ebenfalls entlang solcher geodätische Linien durch die Raumzeit bewegen.
Nun konnte Einstein auch den Gezeiteneffekt logisch erklären: Ein freifallender Kör-per wird deswegen in die Richtung des gravitationsausübenden Objektes gestreckt und senkrecht dazu komprimiert, weil jeder Teil dieses Körpers einer anderen geodätischen Linie durch die Raumzeit folgt. Diese Linien sind zunächst parallel, laufen jedoch mit ab-nehmender Distanz zum gravitationsausübenden Objekt aufeinander zu, was der seitlichen Kompression des freifallenden Objektes entspricht (siehe Anhang IV). Eine Krümmung der Raumzeit entspricht also dem Gezeiteneffekt der Newtonschen Physik. Die Antwort auf die Fragen, warum und wodurch diese Krümmung auftritt und wie sie quantitativ beschrieben werden kann, war ab 1912 der Hauptgegenstand Einsteins Arbeit. Dazu musste er sich mit Hilfe eines befreundeten Mathematikers die sogenannte Differentialgeometrie aneignen, die nach dessen Aussage "ein furchtbar unübersichtliches Gebiet sei, mit dem sich Physiker besser nicht einließen."21 Und so dauerte es bis 1915, als Ein-stein die endgültige Fassung der Allgemeinen Relativitätstheorie präsentierte, deren zehn Feldgleichungen der Gravitation in allen Bezugssystemen gültig sind. Sie drücken die Wechselwirkung zwischen Masse und Raumzeit-Krümmung mathematisch korrekt aus, sagen also neben der gravitativen Zeitdilatation vor allem voraus, wie Masse die Raumzeit krümmt und wie eine Krümmung der Raumzeit das Verteilungsmuster von Masse beein-flusst. Als ersten Beweis für ihre Gültigkeit konnte Einstein nun die Verschiebung des Merkurperihels vollständig erklären. Ebenso sagte er eine Ablenkung des Lichts aufgrund der Raumzeit-Krümmung in der Umgebung der Sonne voraus, die 1919 von dem briti-schen Astrophysiker Sir Arthur Stanley Eddington experimentell bestätigt wurde. Die gravitative Zeitdilatation wurde erst weitaus später gemessen. "1959 führte man an der Universität Harvard ein Experiment durch,"22 das auf dem Mößbauer-Effekt23 beruht . Somit konnte man den Zeitunterschied zwischen einem 22,5 Meter hohen Turm der Universität und dem Erdboden bestimmen. Obwohl der Verzögerungsfaktor des Zeitunterschieds im Bereich von lag, war die gravitative Zeitdilatation nun erstmals experimentell bestätigt.
13Thorne, Kip: Gekrümmter Raum und verbogene Zeit. Lewis Thomas. Bd. 9 der Reihe: The Common-wealth Fund Book Program. - München:(Droemer Knaur) 1994; S. 109
14Thorne, Kip: Gekrümmter Raum und verbogene Zeit. Lewis Thomas. Bd. 9 der Reihe: The Common-wealth Fund Book Program. - München:(Droemer Knaur) 1994; S. 109
15vgl. http://abenteuer-universum.de/merkur.html#rot (22.01.2006)
16Thorne, Kip: Gekrümmter Raum und verbogene Zeit. Lewis Thomas. Bd. 9 der Reihe: The Common-wealth Fund Book Program. - München:(Droemer Knaur) 1994; S. 106
17Thorne, Kip: Gekrümmter Raum und verbogene Zeit. Lewis Thomas. Bd. 9 der Reihe: The Common-wealth Fund Book Program. - München:(Droemer Knaur) 1994; S. 99
18Krauss, Lawrence M.: Die Physik von Star Trek. Wolfgang Jeschke. 6. Auflage. - München:(Wilhelm Heyne Verlag GmbH & Co. KG); S. 41
19vgl. Krauss, Lawrence M.: Die Physik von Star Trek. Wolfgang Jeschke. 6. Auflage. - München:(Wilhelm Heyne Verlag GmbH & Co. KG); S. 40ff
20Thorne, Kip: Gekrümmter Raum und verbogene Zeit. Lewis Thomas. Bd. 9 der Reihe: The Common-wealth Fund Book Program. - München:(Droemer Knaur) 1994; S. 122
21Thorne, Kip: Gekrümmter Raum und verbogene Zeit. Lewis Thomas. Bd. 9 der Reihe: The Common-wealth Fund Book Program. - München:(Droemer Knaur) 1994; S. 126
22Davies, Paul: So baut man eine Zeitmaschine. Eine Gebrauchsanweisung. - München:(Piper Verlag GmbH); S. 30
23vgl. http://de.wikipedia.org/wiki/Robert_Pound (03.01.2006) und http://de.wikipedia.org/wiki/Zeitdilatation (03.01.2006) und
http://de.wikipedia.org/wiki/M%C3%B6%C3%9Fbauer-Effekt (03.01.2006) und
http://www.physik.uni-muenchen.de/leifiphysik/web_ph12/versuche/09photmasse/photmasse.htm (03.01.2006)
2.3. Antimaterie
Eine weitere Rolle bei der physikalischen Analyse von Raumzeit-Reisen spielt die Antimaterie, ein Phänomen, das unter anderem ein Resultat der Speziellen Relativitätstheorie sowie der Quantenmechanik war. Da die Thematik der Antimaterie jedoch nur von untergeordneter Bedeutung für Raumzeit-Reisen sein wird, ist hier keine ausführliche Erläuterung nötig, eine kurze Erklärung findet sich jedoch im Anhang V.
3. Analyse von Raumzeit-Reisen der Science Fiction
Innerhalb der Science Fiction gibt es zahlreiche revolutionäre Techniken, die zu beschreiben mehrere hundert Seiten füllen würde. Deswegen sollen im Folgenden nur die wichtigsten beleuchtet werden, nämlich das Reisen durch die Dimensionen. Bei Bedarf werden weitere physikalische Erscheinungen erläutert.
3.1. Reisen durch den Raum
Raumreisen sind ein elementarer Bestandteil der meisten Science Fiction Geschichten, da häufig große Entfernungen zu überwinden sind. Dabei wird meist zwischen Reisen unterhalb und oberhalb der Lichtgeschwindigkeit unterschieden. Zunächst wird die unterlichtschnelle Raumfahrt betrachtet, da sie einfacher zu verstehen und weniger spekulativ ist.
3.1.1. Unterlichtschnelle Bewegung per Impulsantrieb
Jede erdenkliche Möglichkeit, auf konventionelle Art im Weltraum zu reisen, beruht auf dem Impulserhaltungssatz sowie auf dem Wechselwirkungssatz von Newton. Der Impuls p eines Körpers ist definiert als das Produkt der Masse  des Körpers und seiner Geschwindigkeit v . Die Impulserhaltung besagt, dass in allen abgeschlossenen, von äußeren Kräften freien Systemen (also Inertialsystemen) der Gesamtimpuls erhalten bleibt, formal ausgedrückt durch
des Körpers und seiner Geschwindigkeit v . Die Impulserhaltung besagt, dass in allen abgeschlossenen, von äußeren Kräften freien Systemen (also Inertialsystemen) der Gesamtimpuls erhalten bleibt, formal ausgedrückt durch  , wobei
, wobei  ein einzelner Impuls im System ist. Der Wechselwirkungssatz sagt aus, dass jede Kraft eine Reaktionskraft hervorruft, die den gleichen Betrag hat, jedoch entgegengesetzt gerichtet ist.
Aus diesen beiden Sätzen folgt das Rückstoßprinzip, nach dem auch heutzutage Raketen betrieben werden. Wenn ein Objekt (zum Beispiel eine Rakete) der Masse m1 ein anderes Objekt (zum Beispiel Treibstoff) der Masse m2 in die eine Richtung ausstößt, erfährt das Objekt selber eine Kraft in die andere Richtung. Mit der Formel m1 · v1 = -m2 · v2 kann man die Geschwindigkeiten v1 und v2 der Objekte in Bezug auf den Schwerpunkt des Systems 'Rakete-Treibstoff' leicht berechnen. Die Formel folgt aus der Bedingung p1 = -p2 , das heißt, dass bezüglich des Schwerpunktes des Systems der Gesamtimpuls stets Null ist. Das Minuszeichen drückt aus, dass die Geschwindigkeiten entgegengesetzt sind, was zwingende Konsequenz des Wechselwirkungssatzes ist. Die Geschwindigkeit v1 der Rakete der Masse m1 bezüglich des Schwerpunktes des Systems erhält man durch Um-formung:
ein einzelner Impuls im System ist. Der Wechselwirkungssatz sagt aus, dass jede Kraft eine Reaktionskraft hervorruft, die den gleichen Betrag hat, jedoch entgegengesetzt gerichtet ist.
Aus diesen beiden Sätzen folgt das Rückstoßprinzip, nach dem auch heutzutage Raketen betrieben werden. Wenn ein Objekt (zum Beispiel eine Rakete) der Masse m1 ein anderes Objekt (zum Beispiel Treibstoff) der Masse m2 in die eine Richtung ausstößt, erfährt das Objekt selber eine Kraft in die andere Richtung. Mit der Formel m1 · v1 = -m2 · v2 kann man die Geschwindigkeiten v1 und v2 der Objekte in Bezug auf den Schwerpunkt des Systems 'Rakete-Treibstoff' leicht berechnen. Die Formel folgt aus der Bedingung p1 = -p2 , das heißt, dass bezüglich des Schwerpunktes des Systems der Gesamtimpuls stets Null ist. Das Minuszeichen drückt aus, dass die Geschwindigkeiten entgegengesetzt sind, was zwingende Konsequenz des Wechselwirkungssatzes ist. Die Geschwindigkeit v1 der Rakete der Masse m1 bezüglich des Schwerpunktes des Systems erhält man durch Um-formung:
 ( IV. )
( IV. )
Gewöhnlich will man eine möglichst hohe Geschwindigkeit v1 sowie eine möglichst große Masse m1 der Rakete (große Nutzlast), ferner eine möglichst geringe Treibstoffmenge der Masse m2, damit sie nicht den gesamten Laderaum verbraucht. Um in Formel IV möglichst groß werden zu lassen, muss man jedoch m2 und v2 groß annehmen, da sie im Zähler stehen, und zudem eine geringe Masse m1 vorgeben, die im Nenner steht. Die Bedingungen stehen also genau entgegengesetzt den ursprünglichen Wünschen, was jedoch verständlich ist. Denn je weniger Masse die Rakete hat, desto geringer ist ihre Trägheit und desto leichter lässt sie sich beschleunigen. Ebenso ist die große Masse und Geschwindigkeit des zu emittierenden Treibstoffes logisch, da sie den Impuls erhöhen, der durch den der Rakete wieder ausgeglichen werden muss.
- Die Masse der Rakete wird verkleinert. Diese Möglichkeit wird im folgenden nicht berücksichtigt, denn es ist sinnlos, eine Rakete auszusenden, die keine Nutzlast besitzt.
- Die Masse des auszustoßenden Treibstoffes wird erhöht. Daraus ergeben sich jedoch wiederum Probleme: Tatsächlich kann die Rakete nicht den gesamten Treibstoff auf einmal ausstoßen, wie es in der obigen Formel der Fall wäre. Daraus folgt, dass während der Beschleunigungsphase stets diejenige Masse des Treibstoffes zur Masse der Rakete addiert werden muss, die noch nicht ausgestoßen wurde, also noch in der Rakete aufbewahrt wird. Wenn mehr Treibstoff mitgeführt werden soll, um die Endgeschwindigkeit der Rakete zu erhöhen, dann erhöht sich wiederum die Gesamtmasse, die beschleunigt werden muss. Dafür muss wieder mehr Treibstoff mitgeführt werden, was wieder die Gesamtmasse erhöht und so fort. Lawrence M. Krauss, amerikanischer Professor für Physik und Astronomie an der Case Western University in Cleveland, hat zwar berechnet, dass sich diese Kette nicht ewig fortsetzt24. Man benötigt jedoch zwangsläufig ein Vielfaches der Nutzlast an Treibstoff, um auf Geschwindigkeiten zu beschleunigen, die einen nicht zu vernachlässigenden Bruchteil der Lichtgeschwindigkeit betragen. Natürlich braucht man auch Treibstoff zum Abbremsen vor Ankunft am Reiseziel, was die Masse wiederum erhöht. Oft wird vorgeschlagen, den Treibstoff unterwegs einzufangen, etwa aus kosmischen Nebeln oder Sternentstehungsgebieten. Das würde jedoch auch Impuls kosten, denn die Partikel, die eingesammelt werden, müssen ja ebenfalls auf die Geschwindigkeit der Rakete gebracht werden und ihre Trägheit würde dem entgegenwirken.
Außerdem ist die Materiedichte mit
 bis
bis  im Durchschnitt25 viel zu gering, um nennenswerte Mengen eingefangenen Treibstoff zu erhalten.
im Durchschnitt25 viel zu gering, um nennenswerte Mengen eingefangenen Treibstoff zu erhalten.
- Die Ausstoßgeschwindigkeit wird erhöht. Dies ist eine technische Aufgabe, die man durch neue Antriebssysteme verwirklichen könnte:
So wurde zum Beispiel der Ionenantrieb in Erwägung gezogen. Dabei werden geladene Teilchen in elektrischen Feldern beschleunigt und emittiert. Die geringe Masse der Ionen wird durch ihre hohe Geschwindigkeit wieder ausgeglichen. Um sie zu errei-chen muss jedoch auch eine immense Energie in Teilchenbeschleunigern aufgebracht werden. Außerdem sind leistungsfähige Teilchenbeschleuniger derzeit noch viel zu groß, um in Raumfähren jeglicher Art untergebracht zu werden. Eine weitere Idee, die bisher nur in der Science Fiction benutzt wurde, ist der Antimaterie-Antrieb. Man könnte Antimaterie mit Materie annihilieren, wodurch deren Energie vollständig in Photonen umgewandelt wird. Diese werden mit Lichtgeschwindigkeit ausgestoßen und übertragen so den Impuls . Dies wäre der effizienteste Rückstoß-Antrieb, doch auch dabei ergeben sich Probleme. Die Herstellung der Antimaterie verschlingt nach dem aktuellen Stand der Technik "mindestens eine Million mal"26 mehr Energie als durch die Annihilation frei wird. Derzeit existierende, für die Herstellung von Antimaterie nötige Teilchenbeschleuniger sind überdies viel zu leistungsschwach. So kann man im CERN, der Organisation Européenne pour la Recherche Nucléaire (ehemals: Conseil Européen pour la Recherche Nucléaire) bei Genf lediglich rund 1000 Antiatome pro Stunde einfangen, was Krauss anschaulich so ausdrückt: "Bei diesem Tempo würde es etwas mehr als das Millionenfache vom gegenwärtigen Alter des Weltalls dauern, bis genug Antiatome beisammen sind, um eine Stubenfliege auf annähernd Lichtgeschwindigkeit zu bringen."
In einigen Science Fiction Geschichten wird die Antimaterie unterwegs an Bord des Raumschiffes hergestellt. Diese Möglichkeit ist energetisch gesehen jedoch völlig unsinnig, denn zur Produktion eines Antiteilchens wird stets mehr Energie verbraucht als durch die Annihilation frei wird. Dies folgt aus dem Energieerhaltungssatz. Wäre dies nicht der Fall, würde aus wenig Energie mehr Energie werden, doch wo käme dieser Überschuss dann her? Es wäre eine Energieverschwendung, erst mit vorhandener Energie Antimaterie zu erzeugen, anstatt sie gleich in den Antrieb zu investieren. Wenn man die Antimaterie mitführen muss, stellt sich neben dem obigen Problem der Massenzunahme das Problem ihrer Lagerung. Dazu muss ein starkes magnetisches Feld erzeugt werden und im Fall von Antiatomen müssen diese noch bei einer Temperatur knapp über dem absoluten Nullpunkt von
. Dies wäre der effizienteste Rückstoß-Antrieb, doch auch dabei ergeben sich Probleme. Die Herstellung der Antimaterie verschlingt nach dem aktuellen Stand der Technik "mindestens eine Million mal"26 mehr Energie als durch die Annihilation frei wird. Derzeit existierende, für die Herstellung von Antimaterie nötige Teilchenbeschleuniger sind überdies viel zu leistungsschwach. So kann man im CERN, der Organisation Européenne pour la Recherche Nucléaire (ehemals: Conseil Européen pour la Recherche Nucléaire) bei Genf lediglich rund 1000 Antiatome pro Stunde einfangen, was Krauss anschaulich so ausdrückt: "Bei diesem Tempo würde es etwas mehr als das Millionenfache vom gegenwärtigen Alter des Weltalls dauern, bis genug Antiatome beisammen sind, um eine Stubenfliege auf annähernd Lichtgeschwindigkeit zu bringen."
In einigen Science Fiction Geschichten wird die Antimaterie unterwegs an Bord des Raumschiffes hergestellt. Diese Möglichkeit ist energetisch gesehen jedoch völlig unsinnig, denn zur Produktion eines Antiteilchens wird stets mehr Energie verbraucht als durch die Annihilation frei wird. Dies folgt aus dem Energieerhaltungssatz. Wäre dies nicht der Fall, würde aus wenig Energie mehr Energie werden, doch wo käme dieser Überschuss dann her? Es wäre eine Energieverschwendung, erst mit vorhandener Energie Antimaterie zu erzeugen, anstatt sie gleich in den Antrieb zu investieren. Wenn man die Antimaterie mitführen muss, stellt sich neben dem obigen Problem der Massenzunahme das Problem ihrer Lagerung. Dazu muss ein starkes magnetisches Feld erzeugt werden und im Fall von Antiatomen müssen diese noch bei einer Temperatur knapp über dem absoluten Nullpunkt von  aufbewahrt werden. Nutzt man lediglich Antiprotonen oder andere geladene Antiteilchen, die zwar leichter herzu-stellen sind, wird deren gegenseitige Abstoßung aufgrund der gleichnamigen Ladung derart groß, dass sie nicht mal mehr mit überdurchschnittlich starken Magnetfeldern aufzubewahren wären, nach Krauss "ein logistischer Alptraum"28.
aufbewahrt werden. Nutzt man lediglich Antiprotonen oder andere geladene Antiteilchen, die zwar leichter herzu-stellen sind, wird deren gegenseitige Abstoßung aufgrund der gleichnamigen Ladung derart groß, dass sie nicht mal mehr mit überdurchschnittlich starken Magnetfeldern aufzubewahren wären, nach Krauss "ein logistischer Alptraum"28.Betrachtet man die großen Entfernungen zwischen Himmelskörpern, stößt man auf Probleme, die aus der Reisedauer resultieren: Der nächstgelegene Stern, Proxima Centauri, ist 4,30 Lichtjahre entfernt, was umgerechnet einer Strecke

 entspricht. Durch einfache Anwendung der Bewegungsgleichung
entspricht. Durch einfache Anwendung der Bewegungsgleichung  kann man berechnen, dass das schnellste von Menschen gebaute Objekt, die Voyager I Raumsonde, mit der Geschwindigkeit
kann man berechnen, dass das schnellste von Menschen gebaute Objekt, die Voyager I Raumsonde, mit der Geschwindigkeit  ungefähr für die Zeit
ungefähr für die Zeit 
 unterwegs wäre, um zu Proxima Centauri zu gelangen. Bei bemannten Raumfähren wie dem Space Shuttle würde sich die Reisedauer noch um den Faktor 10 erhöhen. Man muss also die Reisegeschwindigkeit erheblich erhöhen, was - wie bereits diskutiert - sehr schwer ist. Doch gesetzten Falles dies gelingt, hat man sich mit weiteren Problemen auseinander zu setzen, die aus der Speziellen Relativitätstheorie resultieren:
unterwegs wäre, um zu Proxima Centauri zu gelangen. Bei bemannten Raumfähren wie dem Space Shuttle würde sich die Reisedauer noch um den Faktor 10 erhöhen. Man muss also die Reisegeschwindigkeit erheblich erhöhen, was - wie bereits diskutiert - sehr schwer ist. Doch gesetzten Falles dies gelingt, hat man sich mit weiteren Problemen auseinander zu setzen, die aus der Speziellen Relativitätstheorie resultieren:
-
Die unüberwindliche Grenze der Lichtgeschwindigkeit. Sie folgt aus der Geschwindigkeitsabhängigkeit der Masse eines bewegten Objektes gemäß Formel II. Lässt man v gegen
 konvergieren, geht
konvergieren, geht  gegen 1 und damit
gegen 1 und damit  gegen 0. Des weiteren geht dann
gegen 0. Des weiteren geht dann  gegen 0 und
gegen 0 und  gegen Unendlich. Mathematisch ausgedrückt:
gegen Unendlich. Mathematisch ausgedrückt: 
 . Das Verhältnis der geschwindigkeitsabhängigen Masse zur Ruhemasse
. Das Verhältnis der geschwindigkeitsabhängigen Masse zur Ruhemasse  geht also gegen unendlich (siehe Anhang II). Dies bedeutet, dass die Masse eines bewegten Objektes gegen Unendlich geht, je mehr sich seine Geschwindigkeit v an die Lichtgeschwindigkeit c annähert. Je größer die Masse des Objektes wird, umso mehr Kraft muss aufgewendet werden, um es noch weiter zu beschleunigen, da die Trägheit aufgrund der größer werdenden Masse ebenfalls zunimmt. Dies folgt aus dem Grundgesetz der Mechanik F = m · a mit der Beschleunigung a. Je mehr sich v der Lichtgeschwindigkeit c annähert, desto größer wird die Kraft F, die man aufwenden muss, um das Objekt noch mehr in Richtung Lichtgeschwindigkeit zu beschleunigen. Um ein Objekt, das sich schon fast mit der Lichtgeschwindigkeit c bewegt, schließlich vollends auf c zu beschleunigen muss eine unendlich große Kraft erbracht werden. Dies ist nicht möglich, da man dazu unendlich viel Energie bräuchte.
geht also gegen unendlich (siehe Anhang II). Dies bedeutet, dass die Masse eines bewegten Objektes gegen Unendlich geht, je mehr sich seine Geschwindigkeit v an die Lichtgeschwindigkeit c annähert. Je größer die Masse des Objektes wird, umso mehr Kraft muss aufgewendet werden, um es noch weiter zu beschleunigen, da die Trägheit aufgrund der größer werdenden Masse ebenfalls zunimmt. Dies folgt aus dem Grundgesetz der Mechanik F = m · a mit der Beschleunigung a. Je mehr sich v der Lichtgeschwindigkeit c annähert, desto größer wird die Kraft F, die man aufwenden muss, um das Objekt noch mehr in Richtung Lichtgeschwindigkeit zu beschleunigen. Um ein Objekt, das sich schon fast mit der Lichtgeschwindigkeit c bewegt, schließlich vollends auf c zu beschleunigen muss eine unendlich große Kraft erbracht werden. Dies ist nicht möglich, da man dazu unendlich viel Energie bräuchte. Zusätzlich zu dem oben geschilderten Problem, den Treibstoff stets mitbeschleunigen zu müssen, kommt also noch die relativistische Massenzunahme durch hohe Geschwindigkeiten, die es unmöglich macht, sich mit Lichtgeschwindigkeit zu bewegen und die es sehr erschwert, nahe an die Lichtgeschwindigkeit heran zu kommen. In Teilchenbeschleunigern werden zwar regelmäßig Elementarteilchen auf über 99% der Lichtgeschwindigkeit beschleunigt, doch ist deren Ruhemasse naturgemäß um circa 10-30 kleiner als die von 'menschlichen' Raumfahrzeugen.
-
Viele Science Fiction Geschichten handeln von riesigen Imperien, Reichen oder Föderationen, die große Teile von Galaxien beherrschen. Hier sei zum Beispiel das 'Galaktische Imperium' des vom amerikanischen Chemiker Isaac Asimov begonnenen und von zahlreichen Autoren - darunter die Physiker Gregory Benford und David Brin - fortgeführten Foundation-Zyklus genannt. Auch die Raumfahrzeuge der 'Vereinten Föderation der Planeten' aus dem Star Trek Universum können mühelos halbe oder dreiviertel Lichtgeschwindigkeit erreichen. Doch wie wir sehen werden, ist es ein enormes Problem, diese Reiche zu verwalten: Die Zeitdilatation der Speziellen Relativitätstheorie dehnt die Zeit von bewegten Objekten. Wenn also ein Raumschiff von einem Planeten zu einem weit entfernten Ort mit hoher Geschwindigkeit unterwegs ist, müssen nach jeder Ankunft die Uhren synchronisiert werden. Fliegt zum Beispiel ein Raumschiff von der Erde zum 1100 Lichtjahre (
 des Durchmessers der Milchstraße) entfernten Polarstern mit der idealisierten (Vernachlässigung des Beschleunigungs- und Abbremsvorgang) konstanten Geschwindigkeit
des Durchmessers der Milchstraße) entfernten Polarstern mit der idealisierten (Vernachlässigung des Beschleunigungs- und Abbremsvorgang) konstanten Geschwindigkeit  , so vergeht auf der Erde die Zeit
, so vergeht auf der Erde die Zeit  , während für das Raumschiff gemäß Formel I nur die Zeit
, während für das Raumschiff gemäß Formel I nur die Zeit  9,66 · 102 a vergeht. Dies kann zu großem Aufwand führen, denn ein interstellares Reich muss regen Verkehr mit Raumfahrzeugen haben, um verwaltet werden zu können.
Selbst wenn man es schaffen würde, mit
9,66 · 102 a vergeht. Dies kann zu großem Aufwand führen, denn ein interstellares Reich muss regen Verkehr mit Raumfahrzeugen haben, um verwaltet werden zu können.
Selbst wenn man es schaffen würde, mit  zum Polarstern zu fliegen: Während die Reise für das Raumschiff und seine Besatzung nur etwas mehr als 49 Jahre dauern würde, wären auf der Erde etwas mehr als 1100 Jahre vergangen (vgl. explizite Rechnung in Anhang VI). Dort würde man kaum mehr von der Forschungsmission des Raumschiffes wissen, denn es sind bereits viele Generationen vergangen, oder zumindest würde sich niemand mehr auf der Erde dafür interessieren, da die Forschung schon weiter fortgeschritten wäre.
zum Polarstern zu fliegen: Während die Reise für das Raumschiff und seine Besatzung nur etwas mehr als 49 Jahre dauern würde, wären auf der Erde etwas mehr als 1100 Jahre vergangen (vgl. explizite Rechnung in Anhang VI). Dort würde man kaum mehr von der Forschungsmission des Raumschiffes wissen, denn es sind bereits viele Generationen vergangen, oder zumindest würde sich niemand mehr auf der Erde dafür interessieren, da die Forschung schon weiter fortgeschritten wäre.
Doch unabhängig von dem Synchronisationsproblem ist es natürlich sinnlos, Reisen zu unternehmen, die länger als ein Menschenleben dauern. Es wurde vorgeschlagen, riesige, sich selbst versorgende Raumschiffe zu benutzen. Diese 'Generationenschiffe', die auch gerne von Science Fiction Autoren aufgegriffen werden, würden eine eigene Biosphäre beherbergen, in der Menschen leben und sich fortpflanzen, bis die Reise beendet ist. Doch solche Schiffe würden selbstverständlich eine riesige Masse haben, die es noch schwerer macht, das Raumschiff zu beschleunigen, wodurch die Reise noch länger dauert. Davon abgesehen ergeben sich noch unzählige Probleme, wie zum Beispiel diejenigen, welche die NASA hatte, als Wissenschaftler im Projekt 'Biosphere II' versuchten, ein abgeschlossenes, sich selbst versorgendes Ökosystem zu schaffen.
Man muss also die 'Fesseln' der Speziellen Relativitätstheorie ablegen und die Grenze der Lichtgeschwindigkeit überwinden, um das All zu besiedeln. Mit den oben beschriebenen Mitteln kommt man in 'menschlichen' Maßstäben nicht aus dem Sonnensystem heraus. So kommt nicht nur Krauss zu dem Entschluss: "Es muss eine bessere Lösung geben!"29
25vgl. http://de.wikipedia.org/wiki/Universum_%28Astronomie%29 (03.01.2006)
26Krauss, Lawrence M.: Die Physik von Star Trek. Wolfgang Jeschke. 6. Auflage. - München:(Wilhelm Heyne Verlag GmbH & Co. KG); S. 109
27Krauss, Lawrence M.: Jenseits von Star Trek. Die Physik hinter den Ideen der Science Fiction. Wolfgang Jeschke. - München:(Wilhelm Heyne Verlag GmbH & Co KG); S. 49
28 Krauss, Lawrence M.: Jenseits von Star Trek. Die Physik hinter den Ideen der Science Fiction. Wolfgang Jeschke. - München:(Wilhelm Heyne Verlag GmbH & Co KG); S. 50
29Krauss, Lawrence M.: Jenseits von Star Trek. Die Physik hinter den Ideen der Science Fiction. Wolfgang Jeschke. - München:(Wilhelm Heyne Verlag GmbH & Co KG); S. 50
3.1.2. Überlichtschnelle Bewegung
Um das Universum besiedeln zu können, muss man sich also schneller als das Licht bewegen können. Nach der Speziellen Relativitätstheorie ist dies schlichtweg unmöglich, doch die Allgemeine Relativitätstheorie lässt einige Schlupflöcher offen.
3.1.2.1. Warpantrieb
Egal wie verschieden die Namen der überlichtschnellen Raumschiff-Antriebe von Science Fiction Geschichten sind, sie alle müssen auf einem ähnlichen Prinzip beruhen. Die Raumzeit wird verzerrt und weil 'verzerren' dem Englischen 'to warp' entspricht, sprechen die meisten Wissenschaftler vom Warpantrieb, der unter anderem vom mexikanischen Physiker Miguel Alcubierre von der Universidad National Autónoma de México untersucht und mit der Allgemeinen Relativitätstheorie abgestimmt wurde. Wie Krauss hervorhebt, muss man in diesem Kontext eine sehr genaue Ausdrucksweise verwenden, wenn man über Bewegungen nachdenkt. So kann im lokalen Maßstab nichts schneller als das Licht sein, doch global betrachtet ist dies durchaus möglich. Als Beispiel sei unser Universum genannt: Der amerikanische Astronom Edwin Powell Hubble hat 1929 die Fluchtgeschwindigkeit anderer Galaxien ermittelt und dadurch nachgewiesen, dass unser Universum expandiert, weil die Raumzeit sich ausdehnt. Obwohl sich jeder Himmelskörper (also auch die Sonne) in Bezug auf seine lokalen Nachbarn nicht maßgeblich bewegt, kann eine zunehmende Entfernung weit entfernter Objekte gemessen werden, wobei deren Geschwindigkeit in Bezug auf die Sonne umso größer ist, je weiter das betreffende Objekt von ihr entfernt ist. Himmelskörper am Rand des beobachtbaren Universums entfernen sich mit annähernder Lichtgeschwindigkeit voneinander und es wird angenommen, dass unser Universum kurz nach dem Urknall in der inflationären Phase mit Überlichtgeschwindigkeit expandierte. Es kann also weit entfernte Objekte im Universum geben, die sich in Bezug auf ihre lokale Umgebung zwar nicht merklich entfernen, die sich aber global betrachtet mit Überlichtgeschwindigkeit voneinander entfernen. Dies ist der Fall, weil die Raumzeit expandiert.
Dieses Beispiel zeigt, dass überlichtschnelle Bewegung global durchaus möglich ist. Die Frage lautet also nun, ob und wenn ja, wie man die Raumzeit manipulieren könnte, um sich mit Überlichtgeschwindigkeit fortzubewegen. Alcubierre schlug vor, die Raumzeit derart zu krümmen, dass sie vor dem Raumschiff kontrahiert wird und dahinter expandiert30. Das Raumschiff wird also in eine Blase gehüllt, bei der die Raumzeit in der vorderen Blasenwand gestaucht ist und in der hinteren Wand gedehnt. Damit könnte das Raumschiff mit Hilfe der Raumzeit-Blase näher an den Zielort gelangen, da sich die Raumzeit zwischen Raumschiff und Zielort zusammenzieht, und sich weiter vom Startpunkt entfernen, da sich die Raumzeit dazwischen ausdehnt. Währendessen bewegt sich das Raumschiff mit geringer Geschwindigkeit in Bezug auf die nahe Umgebung innerhalb der Blase, wo die Raumzeit nahezu flach, also nicht gekrümmt ist, und vermeidet somit die Tücken der Speziellen Relativitätstheorie. Nach dem Transfer kommt die Raumzeit wieder in die ursprüngliche Geometrie. Die Raumzeit wird also in der hinteren Blasenwand wieder gestaucht und in der vorderen Wand gedehnt, sodass insgesamt wieder der anfängliche Zustand erreicht wird.
Raumzeit kann nur gekrümmt werden, wenn Masse beziehungsweise Energie vorhanden ist. Zusätzlich ist für eine bestimmte Raumzeit-Krümmung eine bestimmte Anordnung der Masse beziehungsweise Energie nötig. Nach Abstimmung der gewünschten Raumzeit-Krümmung mit der Allgemeinen Relativitätstheorie stellte sich Folgendes heraus: Es ist Materie notwendig, die negative Energiedichte besitzt. Solche Materie, die nach dem Amerikaner Kip Stephen Thorne vom California Institute of Technology exotische Materie genannt wird, existiert nach bisheriger Erkenntnis nirgends im beobachtbaren Universum, in dem stets Materie mit positiver Energiedichte gemessen wurde. Die exotische Materie darf jedoch nicht mit Antimaterie verwechselt werden. Diese wirkt sehr wahrscheinlich gravitationell wie 'normale' Materie ebenfalls anziehend, im Gegensatz zur exotischen Materie, die "auf einem gewissen Niveau [...] andere Materie gravitationell abstößt."31 Negative Energiedichte wurde schon mehrfach nachgewiesen. So kann man im Vakuum stets sogenannte Vakuumfluktuationen messen, die von den Gesetzen der Quantenmechanik verlangt werden. Dies sind extrem schwache und kurzzeitige elektromagnetische Schwingungen, die nie "vollständig aus einem Raumgebiet"32 entfernt werden können. Selbst wenn man jede Art von Energie aus einem Raumbereich heraus hält, fluktuiert das elektromagnetische Feld. Es hat mancherorts positive Energie, woanders dagegen negative Energie. Die Differenzen gleichen sich jedoch schnell wieder aus, was letztendlich der Grund für das Fluktuieren ist. Thorne vergleicht dies mit Banken, die auch Kredite aufnehmen, welcher der negativen Energie entsprechen, jedoch nach einer bestimmten Zeit zurückfordern. Insgesamt ist die mittlere Energie also Null, was die Vakuumfluktuationen unabhängig von äußeren Einflüssen macht.
Vakuumfluktuationen machen sich zum Beispiel auch beim sogenannten Casimir-Effekt bemerkbar. Dabei werden zwei verspiegelte Platten parallel zueinander mit nur dem Bruchteil eines Millimeters Abstand im Vakuum bei der Temperatur des absoluten Nullpunktes von -273°C aufgestellt. Da Vakuumfluktuationen überall stattfinden, fluktuieren auch zwischen den beiden Platten elektromagnetische Felder, jedoch nur solche, bei denen "die Wellenlänge ein ganzzahliger Bruchteil des Abstands der Platten ist."33 Der Plattenabstand muss also ein ganzzahliges Vielfaches der Wellenlänge betragen, damit elektromagnetische Felder zwischen den Platten fluktuieren können. Diese Einschränkung auf die Existenz der elektromagnetischen Felder findet außerhalb der Platten nicht statt. Somit sind außerhalb der Platten mehr elektromagnetische Schwingungen zu finden als innerhalb. Gemäß dem Welle-Teilchen-Dualismus kann jede elektromagnetische Welle auch als Photon verstanden werden, wobei die durch Vakuumfluktuationen hervorgerufenen Photonen als virtuelle Photonen bezeichnet werden. Also findet man außerhalb mehr virtuelle Photonen als innerhalb. Dadurch entsteht ein Druck von außen auf die Platten, da von außen mehr virtuelle Photonen gegen die Platten stoßen als von innen. Diesen Effekt sagte der niederländische Nobelpreisträger Hendrik Casimir bereits 1948 voraus; aufgrund der zum Nachweis erforderlichen komplizierten Messungen konnte er aber erst 1997 experimentell bestätigt werden. Da außerhalb der Platten Vakuum ist und somit die Energiedichte verschwindet, innen aber weniger als Null ist, ist innen die Energiedichte negativ. Diese Erkenntnis zeigt, dass durchaus negative Energiedichte möglich ist. Ob es Materie mit negativer Energiedichte gibt und wenn ja, wie man sie in großem Stil herstellen kann, bleibt offen. "Die bisherigen Anzeichen sind nicht besonders ermutigend."34
Davon abgesehen ergaben sich noch mehr Probleme, die entstanden, als in den 90er Jahren weitere Physiker den Warpantrieb genauer unter die Lupe nahmen und mit allen physikalischen Gesetzen abzustimmen versuchten:
So wurde beispielsweise berechnet, dass, um die Raumzeit-Blase längere Zeit aufrecht zu erhalten, rund "zehn Milliarden Mal mehr Energie, als die gesamte sichtbare Masse des Universums"35 gespeichert hat, notwendig ist. Obwohl Alcubierre die Korrektheit der Berechnung anzweifelt, zeigt das Ergebnis, dass außerordentlich viel Energie von Nöten ist, um die gewünschte Raumzeit-Krümmung zu ermöglichen.
Neben weiteren vorwiegend technischen Problemen ist folgender Sachverhalt unmöglich zu umgehen: Um die Raumzeit den Wünschen entsprechend zu krümmen, muss für eine ganz bestimmte Materieanordnung beziehungsweise -verteilung gesorgt werden. Und um diese Anordnung zu erreichen, muss "mindestens ein Signal den ganzen Weg durch diesen Raum"36 geschickt werden, denn durch irgendeine Information muss die Materie natürlich beeinflusst werden, um die erwünschte Formation einzunehmen. Es dauert also mindestens so lange, wie der betreffende Ort in Lichtjahren entfernt ist, falls noch niemand am Zielort ist und die Materieanordnung vollzieht. Während Alcubierre auf die in der Entwicklung begriffene Theorie der Quantengravitation, eine Vereinheitlichung von Relativitätstheorie und Quantenmechanik, hofft und sich von ihr neue Erkenntnisse in Sachen Warpantrieb verspricht, sehen andere Physiker weitere Anstrengungen und Forschung in die Warptechnologie als umsonst an. "Das letzte Warp-Wort ist also noch nicht gesprochen."37
3.1.2.2. Wurmlöcher
Eine ältere Idee, durch Raumzeit-Krümmung die Grenze der Lichtgeschwindigkeit zu umgehen, besteht in sogenannten Wurmlöchern. Ein Wurmloch ist eine Verbindung zwischen zwei Punkten der Raumzeit, also ein Tunnel, der durch Krümmung der Raumzeit entsteht. Es kann sowohl als Abkürzung zwischen zwei Regionen der Raumzeit dienen als auch als Verbindung zweier Universen. Ähnlich wie bei Schwarzen Löchern ist die Raumzeit in großem Abstand fast flach, das heißt ohne Krümmung. "Nähert man sich dem Loch, nimmt die Krümmung zu,"38 bis sie im sogenannten Schlund am stärksten ist. Dahinter nimmt sie wieder ab. Das Wurmloch öffnet sich und verbindet somit zwei Regionen der Raumzeit durch einen vierdimensionalen röhrenartigen Tunnel, der natürlich "kein wirkliches Loch durch etwas ist, sondern aus Raum besteht"39 . Wurmlöcher kann man sich vereinfacht an einem zweidimensionalen Modell vorstellen. Anhang VII zeigt dies allgemein anhand einer Gummihaut, bei der die Krümmung in die dritte Dimension eingebettet ist. Auf ähnliche Art veranschaulichte sie auch der amerikanische Physiker John Archibald Wheeler, der in den 50er Jahren maßgeblich den Namen Wurmloch prägte, da er sie "mit den Kanälen von Würmern in Äpfeln verglichen"40 hat.
Wurmlöchern ähnliche Phänomene wurden bereits seit der Publikation der Allgemeinen Relativitätstheorie in Erwägung gezogen. Da diese älteren Gedankenkonstrukte jedoch für Raumzeit-Reisen keine praktische Bedeutung haben, wird nur im Anhang VIII eine kurze Zusammenfassung dargestellt.
Der Anstoß zu einer Diskussion über nutzbare Wurmlöcher kam 1984 von dem amerikanischen Professor für Astronomie und Weltraumwissenschaften der Cornell University Carl Sagan, der das Skript des Science Fiction Romans Contact an seinen Freund Kip Thorne schickte, der die Geschichte auf physikalische Stimmigkeit überprüfen sollte. Sagan wollte die Protagonisten durch einen Tunnel zwischen Schwarzen Löchern reisen lassen, auf den sie von einer fremden Zivilisation aufmerksam gemacht wurden. Thorne kannte natürlich die in Anhang VIII beschriebenen Probleme, doch er wollte seinen Freund nicht enttäuschen. So gelangte Thorne nach Jahren der Vergessenheit erneut zu Wurmlöchern. Bis dahin hatte noch kein seriöser Physiker ernsthaft in Erwägung gezogen, Wurmlöcher mit Raumschiffen zu durchqueren. Doch Thorne versuchte, die Feldgleichungen der allgemeinen Relativitätstheorie auf Wurmlöcher anzuwenden. "Er wusste, welche Raumgeometrie erforderlich war - sie sollte die Gestalt eines Wurmloches mit zwei sphärischen Mündungen besitzen."41 Zudem sollte das Wurmloch längere Zeit stabil bleiben und groß genug sein, um die Durchquerung eines Raumschiffes zuzulassen. Ferner mussten die Gezeitenkräfte beim Ein- und Austritt in das Wurmloch klein sein und es durfte nicht von einem Ereignishorizont umhüllt sein. Es musste sich also grundlegend von dem in Anhang VIII beschriebenen Typ auf der Basis Schwarzer Löcher unterscheiden. Thorne stellte schließlich fest, dass dazu Energie nötig war, die geringstenfalls in einigen Bezugssystemen negativen Wert hat. Wurmlöcher benötigen also wie auch der Warpantrieb Energie beziehungsweise Masse mit gravitationell abstoßender Wirkung. Dies ist insofern logisch, da Wurmlöcher die austretende Materie und Strahlung defokussieren, im Gegensatz zu Schwarzen Löchern, bei denen jegliches eintretende Material in der Singularität konvergiert. Dies ist auch der Grund, warum Wurmlöcher wie Zerstreuungslinsen wirken. Einfallende Strahlung wird zunächst gebündelt und fächert sich beim Austritt wieder auf. Es ist also negative Energiedichte nötig, um das Wurmloch stabil zu halten. Der Schlund muss durch die abstoßende Gravitation offen gehalten werden, damit er sich nicht abschnürt und zwei Singularitäten hinterlässt.
So stieß Thorne also erstmals auf eine physikalisch plausible Möglichkeit, per Wurmloch durch die Raumzeit zu reisen. Damit löste er bei vielen Kollegen Interesse aus und obwohl es auch viele Physiker gibt, "die vor Schrecken ihre Hände über dem Kopf zusammenschlagen angesichts solcher Verrücktheiten"42 , belegt "die große Zahl wissenschaftlicher Veröffentlichungen zum Thema"43 Wurmlöcher, dass diese nicht nur auf Spekulation beruhen. Sie technisch nutzbar zu machen, ist jedoch wie auch beim Warpantrieb sehr schwierig. Es gibt drei Arten, Wurmlöcher zu erzeugen:
- Falls Wurmlöcher bereits im Universum existieren, könnte man sie anhand ihrer Art, Licht wie eine Zerstreuungslinse zu defokussieren, über weite Entfernungen aufspüren. Ein solches Wurmloch wäre natürlich kaum zu beeinflussen, da es sich höchstwahrscheinlich fern vom menschlichen Einflussbereich aufhielte und "sich kaum kontrollieren ließe, wohin es führt."44
- Eine andere Möglichkeit bedient sich klassischer Mittel. Die Raumzeit wird derart gekrümmt und aufgeschnitten, dass sie sich zu einem Wurmloch verbinden lässt. Doch bis man die aufgeschnittene Raumzeit zusammenbringt, hat sie einen offenen Rand. "Ein freigelegter Rand dieser Art, der zur Herstellung eines passierbaren Wurmloches erforderlich ist, wäre eine nackte Singularität"45 , die es gemäß der Hypothese der kosmischen Zensur des britischen Mathematikers Sir Roger Penrose nicht geben darf. Es scheint also zweifelhaft, ob dieses Vorgehen gelingen wird.
- Die nach Meinung der meisten Physiker erfolgversprechendste Art, Wurmlöcher zu erzeugen, beruht auf einem quantenmechanischen Weg. Dabei werden submikroskopische virtuelle Wurmlöcher aus dem sogenannten Quantenschaum (siehe Anhang IX) hervorgeholt und drastisch vergrößert. Die noch unvollkommene Theorie der Quantengravitation sagt solche virtuellen Wurmlöcher in Größenordnung der Planck-Länge von
 voraus. Sie entstehen und vergehen aufgrund von quantenphysikalischen Ereignissen innerhalb der Planck-Zeit von
voraus. Sie entstehen und vergehen aufgrund von quantenphysikalischen Ereignissen innerhalb der Planck-Zeit von  überall, andauernd, spontan und zufällig aus der Raumzeit. Wie in Kapitel 3.1.2.1. erklärt, gibt es ständig Vakuumfluktuationen, bei denen elektromagnetische Felder kurzzeitig auftreten und wieder verschwinden. Dabei gilt, dass die enthaltene Energie umso größer ist, je kürzer die Fluktuationen andauern und je kleiner der Raum ist, auf den sie beschränkt sind. Bei Fluktuationen mit einer Dauer der Planck-Zeit kann die aufgenommene Energie derart groß sein, "daß deren Masse die Raumzeit beträchtlich verzerrt und zu komplexen Strukturen verformt."46 Die Raumzeit ist also auf dieser kleinsten physikalischen Skala von virtuellen Wurmlöchern durchsetzt, die ihr eine schaumartige Struktur verleihen. So kam Wheeler auf die Bezeichnung Quantenschaum, den er "als ein brodelndes Meer von geometrischen Möglichkeiten"47 bezeichnete.
Solche virtuellen Wurmlöcher könnte man mit negativer Energie füllen, was zur sogenannten inflationären Expansion führt. Sie würden zu makroskopischen Wurmlöchern vergrößert werden und durch die negative Energie auch als permanente Wurmlöcher stabil bleiben.
überall, andauernd, spontan und zufällig aus der Raumzeit. Wie in Kapitel 3.1.2.1. erklärt, gibt es ständig Vakuumfluktuationen, bei denen elektromagnetische Felder kurzzeitig auftreten und wieder verschwinden. Dabei gilt, dass die enthaltene Energie umso größer ist, je kürzer die Fluktuationen andauern und je kleiner der Raum ist, auf den sie beschränkt sind. Bei Fluktuationen mit einer Dauer der Planck-Zeit kann die aufgenommene Energie derart groß sein, "daß deren Masse die Raumzeit beträchtlich verzerrt und zu komplexen Strukturen verformt."46 Die Raumzeit ist also auf dieser kleinsten physikalischen Skala von virtuellen Wurmlöchern durchsetzt, die ihr eine schaumartige Struktur verleihen. So kam Wheeler auf die Bezeichnung Quantenschaum, den er "als ein brodelndes Meer von geometrischen Möglichkeiten"47 bezeichnete.
Solche virtuellen Wurmlöcher könnte man mit negativer Energie füllen, was zur sogenannten inflationären Expansion führt. Sie würden zu makroskopischen Wurmlöchern vergrößert werden und durch die negative Energie auch als permanente Wurmlöcher stabil bleiben.
Egal auf welche Art man ein Wurmloch erzeugt, in jedem Fall muss es stabilisiert werden. Die Menge an negativer Energie, die man dazu benötigt, ist jedoch wie auch beim Warpantrieb extrem groß. So benötigte man, um ein Wurmloch offen zu halten, dessen Schlund einen Radius von nur einem Meter hat, einen Betrag an negativer Energie, der gleich der abgestrahlten Energie von "zehn Milliarden Sterne[n] in einem Jahr"48 ist. Bei Vergrößerung des Schlund-Durchmessers würde sich die benötigte negative Energie direkt proportional dazu erhöhen. In allen drei Fällen des Reisens durch den Raum - dem Antrieb auf Basis von Impulsübertragung, dem Warpantrieb und dem Passieren von Wurmlöchern - scheint die Verwirklichung also vor allem von energetischen Problemen abzuhängen. Die Gesetze der Physik, vor allem der beiden Relativitätstheorien, scheinen sie jedoch grundsätzlich nicht auszuschließen.
39Vaas, Rüdiger: Tunnel durch Raum und Zeit. - Stuttgart:(Franckh-Kosmos Verlags-GmbH & Co. KG) 2005; S. 142
40Vaas, Rüdiger: Tunnel durch Raum und Zeit. - Stuttgart:(Franckh-Kosmos Verlags-GmbH & Co. KG) 2005; S. 133
41Davies, Paul: So baut man eine Zeitmaschine. Eine Gebrauchsanweisung. - München:(Piper Verlag GmbH); S. 83
42Vaas, Rüdiger: Tunnel durch Raum und Zeit. - Stuttgart:(Franckh-Kosmos Verlags-GmbH & Co. KG) 2005; S. 138
43Vaas, Rüdiger: Tunnel durch Raum und Zeit. - Stuttgart:(Franckh-Kosmos Verlags-GmbH & Co. KG) 2005; S. 138
44Vaas, Rüdiger: Tunnel durch Raum und Zeit. - Stuttgart:(Franckh-Kosmos Verlags-GmbH & Co. KG) 2005; S. 139
45Davies, Paul: So baut man eine Zeitmaschine. Eine Gebrauchsanweisung. - München:(Piper Verlag GmbH); S. 97
46Davies, Paul: So baut man eine Zeitmaschine. Eine Gebrauchsanweisung. - München:(Piper Verlag GmbH); S. 98
47Vaas, Rüdiger: Tunnel durch Raum und Zeit. - Stuttgart:(Franckh-Kosmos Verlags-GmbH & Co. KG) 2005; S. 142
48Vaas, Rüdiger: Tunnel durch Raum und Zeit. - Stuttgart:(Franckh-Kosmos Verlags-GmbH & Co. KG) 2005; S. 145
3.2. Reisen durch die Zeit
Die erste Science Fiction Geschichte, die von Zeitreisen handelt und diese als Reisen durch die vierte Dimension auffasst, stammt von dem englischen Schriftsteller Herbert George Wells. Die Zeitmaschine wurde 1895 publiziert, also 13 Jahre bevor Minkowski Raum und Zeit zur Raumzeit vereinheitlichte. Damals also topaktuell, ist sie heute wissenschaftlich nicht mehr haltbar. Im Gegensatz zu Wells Zeitmaschine, die einem mechanischen Gefährt ähnelt, das den Zeitfluss außerhalb des Reisenden und der Zeitmaschine gleichsam im Schnelldurchlauf vor- und zurückspulen kann, sind alle wissenschaftlich plausiblen Arten von Zeitmaschinen "Teil der kosmischen Architektur"49 und beruhen als Teil der Raumzeit hauptsächlich auf den Relativitätstheorien. Den ersten Hinweis auf Zeit-reisen, die in der Fachterminologie 'geschlossene zeitartige Kurven' genannt werden, fand der niederländische Physiker Willem Jacob van Stockum im Jahre 1937. Durch die Allgemeine Relativitätstheorie gelangte er zu dem Ergebnis, dass Zeitreisen möglich sind, wenn "ein Beobachter sich in einer Umlaufbahn um einen rotierenden Zylinder befände."50 1976 vervollständigte Frank Tipler, Professor der mathematischen Physik an der Tulane University in New Orleans, diese Theorie, indem er erkannte, dass der Zylinder eine möglichst hohe Dichte haben und mindestens mit halber Lichtgeschwindigkeit rotieren sollte. Zur mathematischen Erleichterung nahmen van Stockum und Tipler jedoch einen unendlich langen Zylinder an, und da dazu unendlich viel Materie notwendig wäre, war klar, dass dieses Modell unrealistisch war. Es zeigte dennoch, dass "die Allgemeine Relativitätstheorie Zeitreisen in die Vergangenheit nicht explizit ausschloß."51 Auch Kurt Gödel, ein österreichischer Mathematiker und Philosoph, der wie auch Einstein am Institute for Advanced Study in Princeton arbeitete, zeigte dies 1949. Gäbe es ein "Universum mit konstanter, überall gleich beschaffener Energiedichte ohne Druck, das rotiert und sich nicht ausdehnt"52 , dann ließen sich Bahnen finden, die in die Vergangenheit führten. Doch dieses Universum unterscheidet sich fundamental von dem Unsrigen, das nicht rotiert aber expandiert. Trotzdem ist die Bedeutung des Gödelschen Universums enorm, da es "zum Ausgangspunkt für eine Reihe wichtiger Entwicklungen auf dem Gebiet der Allgemeinen Relativitätstheorie"53 wurde. Heute gibt es viele Vorschläge, die Zeitreisen theoretisch ermöglichen. Die plausibelsten werden nun näher beleuchtet.
50Davies, Paul: So baut man eine Zeitmaschine. Eine Gebrauchsanweisung. - München:(Piper Verlag GmbH); S. 49
51Davies, Paul: So baut man eine Zeitmaschine. Eine Gebrauchsanweisung. - München:(Piper Verlag GmbH); S. 50
52Krauss, Lawrence M.: Die Physik von Star Trek. Wolfgang Jeschke. 6. Auflage. - München:(Wilhelm Heyne Verlag GmbH & Co. KG); S. 64
53Vaas, Rüdiger: Tunnel durch Raum und Zeit. - Stuttgart:(Franckh-Kosmos Verlags-GmbH & Co. KG) 2005; S. 194
3.2.1. Reisen mittels Zeitdilatation
Aus der Speziellen Relativitätstheorie folgt, dass man auf eine ganz einfache Weise Zeitreisen in die Zukunft unternehmen kann. Die Zeitdilatation führt zur Dehnung der Zeit von bewegten Bezugssystemen nach den in Kapitel 2.1. beschriebenen Gesetzen. Die gemessene Zeit in bewegten Systemen S' ist immer kürzer als die in ruhenden Systemen S, da der Faktor  stets größer als eins ist. Während sich also jemand relativ zum System bewegt, vergeht in S mehr Zeit als in S'. Wenn die sich bewegende Person sich dann relativ zu S nicht mehr bewegt, ist sie in der Zukunft von S, da im System S' insgesamt eine längere Zeitspanne vergangen ist als in . Oft wird dies am Beispiel des sogenannten Zwillingseffekts erklärt: Ein Zwilling steigt in ein Raumschiff und fliegt mit 99% der Lichtgeschwindigkeit zu einem Stern, der zehn Lichtjahre entfernt ist. Mit
stets größer als eins ist. Während sich also jemand relativ zum System bewegt, vergeht in S mehr Zeit als in S'. Wenn die sich bewegende Person sich dann relativ zu S nicht mehr bewegt, ist sie in der Zukunft von S, da im System S' insgesamt eine längere Zeitspanne vergangen ist als in . Oft wird dies am Beispiel des sogenannten Zwillingseffekts erklärt: Ein Zwilling steigt in ein Raumschiff und fliegt mit 99% der Lichtgeschwindigkeit zu einem Stern, der zehn Lichtjahre entfernt ist. Mit  und
und  ergibt sich für die Dauer der von der Erde aus gemessen Zeit
ergibt sich für die Dauer der von der Erde aus gemessen Zeit  . Da der Zwilling für den Rückflug wieder 10,1 Jahre braucht, kommt er also wieder auf der Erde an, nachdem dort die Zeit
. Da der Zwilling für den Rückflug wieder 10,1 Jahre braucht, kommt er also wieder auf der Erde an, nachdem dort die Zeit  vergangen ist. Sein Zwillingsbruder, der auf der Erde zurückgeblieben ist, ist also um 20 Jahre gealtert. Der Raumfahrer dagegen hat sich mit 99% der Lichtgeschwindigkeit fortbewegt. Für ihn ist nur die Zeitspanne
vergangen ist. Sein Zwillingsbruder, der auf der Erde zurückgeblieben ist, ist also um 20 Jahre gealtert. Der Raumfahrer dagegen hat sich mit 99% der Lichtgeschwindigkeit fortbewegt. Für ihn ist nur die Zeitspanne  vergangen. Er ist also um knappe 3 Jahre gealtert. Der raumfahrende Zwilling ist also nun
vergangen. Er ist also um knappe 3 Jahre gealtert. Der raumfahrende Zwilling ist also nun  jünger als sein auf der Erde stationärer Bruder; er ist in dessen Zukunft. Auf diese Art kann man in kürzester Zeit beliebig weit in die Zukunft reisen, wenn man nur ausreichend nahe an die Lichtgeschwindigkeit herankommt. So könnte man das Jahr 2496 innerhalb einer Flugzeit von rund 8 Tagen erreichen, wenn man sich mit 99,99999999% der Lichtgeschwindigkeit fortbewegt (vgl. explizite Rechnung in Anhang X). Betont sei jedoch, dass man durch Zeitdilatation nur in die Zukunft reisen kann, nicht in die Vergangenheit. "Bewegung mit hoher Geschwindigkeit folgt einer Einbahnstraße in die Zukunft."54
jünger als sein auf der Erde stationärer Bruder; er ist in dessen Zukunft. Auf diese Art kann man in kürzester Zeit beliebig weit in die Zukunft reisen, wenn man nur ausreichend nahe an die Lichtgeschwindigkeit herankommt. So könnte man das Jahr 2496 innerhalb einer Flugzeit von rund 8 Tagen erreichen, wenn man sich mit 99,99999999% der Lichtgeschwindigkeit fortbewegt (vgl. explizite Rechnung in Anhang X). Betont sei jedoch, dass man durch Zeitdilatation nur in die Zukunft reisen kann, nicht in die Vergangenheit. "Bewegung mit hoher Geschwindigkeit folgt einer Einbahnstraße in die Zukunft."54
Doch wie in Kapitel 3.1.1. klar wurde, schafft man es aus energetischen Gründen nicht, nahe genug an die Lichtgeschwindigkeit heran zu kommen. Bei einer Fluggeschwindigkeit von 10% der Lichtgeschwindigkeit, was noch weit über den heutzutage möglichen Höchstgeschwindigkeiten von realen Raumfahrzeugen liegt, wäre der 'Zeitgewinn' bei der Flugdauer  für den Zeitreisenden nur
für den Zeitreisenden nur  Er wäre also gerade einmal etwas mehr als
Er wäre also gerade einmal etwas mehr als  Stunden in der Zukunft.
Stunden in der Zukunft.
Eine andere Möglichkeit in die Zukunft zu gelangen beruht auf der gravitativen Zeitdi-latation aus Einsteins Allgemeiner Relativitätstheorie. Wie in Kapitel 2.2. erklärt wurde, verstreicht die Zeit in gekrümmter Raumzeit langsamer als in flacher. In der Nähe von großen Masse- oder Energieansammlungen tickt eine Uhr also langsamer als eine im Weltraum fern von jeglicher Materie. In diesem Zusammenhang bedeutet 'große Masse' allerdings mindestens die Masse von Himmelskörpern wie zum Beispiel Sternen. Im Universum gibt es weitaus massivere Objekte, etwa Neutronensterne oder Schwarze Löcher. Deren Dichte ist derart groß, dass man vergleichsweise nahe an den Massenschwerpunkt herankommt. Je größer die Dichte und je näher man dem Schwerpunkt kommt, desto größer ist die erfahrene Zeitdilatation. Auf der Oberfläche eines durchschnittlichen Neutronensterns, dessen Gravitation so groß ist, dass sämtliche Atome zu Neutronen zerquetscht werden, "würde eine Uhr um ungefähr 30 Prozent langsamer laufen als auf der Erde."55
Hält sich ein Zeitreisender also sieben Tage dort auf, sind auf der Erde schon zehn vergangen. Nach seiner Rückkehr wäre er folglich drei Tage in der Zukunft.
Bei Schwarzen Löchern ist dieser Effekt viel extremer. Im Zentrum eines jeden Schwarzen Loches sitzt eine Singularität, die vermutlich eine unendlich große Dichte hat. Deswegen steht die Zeit innerhalb einer gewissen Distanz zur Singularität von außen betrachtet still, da hier auch die Krümmung unendlich ist. Hält man sich dort einen einzelnen Augenblick lang auf, ist "im umliegenden Universum eine ganze Ewigkeit verstrichen."56 Für eine Zeitreise ist es jedoch völlig ausreichend, sich in die Nähe eines Schwarzen Loches zu begeben. Bei einem stellaren Schwarzen Loch von zehn Sonnenmassen verstreicht die Zeit beispielsweise einen Zentimeter "über dem Horizont sechsmillionenmal langsamer als in großer Entfernung vom Horizont"57. Hält man sich dort eine Minute lang auf, sind auf der Erde bereits 6000000 Minuten oder 11,4 Jahre vergangen.
Doch auch diese Möglichkeit, in die Zukunft zu reisen, wird vermutlich nie Wirklichkeit werden. Es steht zwar außer Frage, dass diese Art des Zeitreisens theoretisch funktioniert, doch kein erdenkliches Material, geschweige denn der Mensch selbst, könnte den großen Gezeitenkräften standhalten, die der Aufenthalt in der Nähe großer Massezentren mit sich brächte. Auch aus anderen Gründen wäre es unmöglich, durch gravitative Zeitdilatation in die Zukunft zu reisen. Hier sei nur die extrem energiereiche Strahlung genannt, die beim Einfall auf massereiche Objekte entsteht. Genau die sind jedoch nötig, um erwähnenswert in die Zukunft zu gelangen. Auf der Erde ist die Zeitdilatation so gering, dass sie nur mit hochpräzisen Atomuhren gemessen werden kann, für Zeitreisen also nicht ausreichend.
55Davies, Paul: So baut man eine Zeitmaschine. Eine Gebrauchsanweisung. - München:(Piper Verlag GmbH); S. 35
56Davies, Paul: So baut man eine Zeitmaschine. Eine Gebrauchsanweisung. - München:(Piper Verlag GmbH); S. 59
57Thorne, Kip: Gekrümmter Raum und verbogene Zeit. Lewis Thomas. Bd. 9 der Reihe: The Common-wealth Fund Book Program. - München:(Droemer Knaur) 1994; S. 112
3.2.2. Reisen mittels Wurmlöcher
Gewiss könnte man also durch Ausnutzen der physikalisch erwiesenen Zeitdilatation in die Zukunft gelangen. In die Vergangenheit allerdings nicht. Dieses für Science Fiction Autoren hochinteressante Thema ließe sich theoretisch jedoch anders bewerkstelligen.
Wurmlöcher können nicht nur als abkürzende Tunnel durch den Raum, sondern auch durch die Zeit verwendet werden, und zwar sowohl in die Zukunft als auch in die Vergangenheit. Diese Idee hatte ebenfalls Kip Thorne, als er Wurmlöcher in den späten 80er Jahren näher überdachte.
Die beiden Öffnungen eines Wurmloches vermögen nicht nur zwei verschiedene im äußeren Universum weit entfernte Orte durch einen kürzeren Tunnel zu verbinden, sondern auch zwei im äußeren Universum verschiedene Zeiten. Dazu müssten diese Zeiten aus einer Sichtweise im Wurmloch aber identisch sein, woraus wiederum folgt, dass sich die Zeit innerhalb des Wurmloches anders fortsetzt als außerhalb des Wurmloches, also im äußeren Universum. "Von außen betrachtet ist der Zeitfluß verschieden, von innen gesehen ist er gleich."58 Aus der Speziellen Relativitätstheorie folgt, dass es zu dieser Situation kommt, wenn sich die Wurmloch-Öffnungen zuvor von außen betrachtet in verschiedenen Bezugssystemen befanden. Da die Zeiten, die die beiden Öffnungen des Wurmloches verbinden, vom Wurmloch aus gleich sind, heißt das ebenso, dass die Öffnungen vom Wurmloch aus betrachtet im selben Bezugssystem enthalten waren.
Zusammenfassend kann gesagt werden, dass sich die beiden Öffnungen des Wurmloches von innen im selben Bezugssystem, von außen in unterschiedlichen Bezugssystemen befinden müssen, um einen unterschiedlichen Zeitfluss innerhalb und außerhalb hervorzurufen. Dies wird auf einfache Weise erreicht, indem eine Öffnung zum Beispiel durch den Raum bewegt wird, die andere dagegen fixiert bleibt. Dadurch befinden sich die beiden Öffnungen in unterschiedlichen Bezugssystemen. Die Länge des Wurmloches selbst bleibt dessen ungeachtet konstant, wodurch sich die Öffnungen vom Wurmloch aus betrachtet im gleichen Bezugssystem befinden. Die bewegte Öffnung erfährt nun Zeitdilatation: Je größer die Geschwindigkeit ist, desto größer ist der Faktor zur Dehnung der Zeit. Bewegt sich eine Öffnung beispielsweise mit 99,999625% der Lichtgeschwindigkeit bezüglich der anderen 24 Stunden lang, so vergeht in der Zeitrechnung der stationären Öffnung ein ganzes Jahr (vgl. explizite Rechnung in Anhang XI). Bringt man die Öffnungen nach der Bewegung - in der Zeitrechnung der stationären Öffnung also nach einem Jahr, in der Zeitrechnung der bewegten Öffnung nach einem Tag - wieder nahe beieinander zur Ruhe, so befindet sich die bewegte Öffnung analog zum Zwillingseffekt 364 Tage in der Zukunft der stationären Öffnung. Darum gelangt man um 364 Tage in die Vergangenheit, wenn man das Wurmloch von der bewegten zur stationären Öffnung durchquert und dementsprechend um 364 Tage in die Zukunft, wenn man es von der stationären zur bewegten Öffnung durchquert.
Natürlich ist dieses Verfahren nicht nur mit Zeitdilatation aufgrund hoher Geschwindigkeit, sondern auch mit der gravitativen Zeitdilatation vorstellbar. Die Wurmloch-Öffnung, die später die Pforte in der Zukunft sein soll, muss lediglich in der Nähe eines starken Gravitationsfeldes platziert sein und erfährt auch hier entsprechend dem in Kapitel 2.2. geschilderten Effekt eine Dehnung der Eigenzeit, gerät also in die Zukunft der anderen Öffnung. Von dem Gravitationsfeld entfernt wirkt das Wurmloch sodann als Verbindung zweier Zeiten und kann in beide Richtungen durchquert werden. Unabhängig von der Technik zum Herstellen der Zeitdilatation wird es jedoch niemals gelingen, "in eine Vergangenheit zu reisen, die weiter zurückliegt, als der Zeitpunkt, da das Wurmloch erstmals zu einer Zeitmaschine wurde."59 Dies ist insofern logisch, weil die Wurmloch-Öffnungen vor der Anwendung der Zeitdilatation noch keine Zeitdifferenz hatten. Dem Reisen in die Zukunft ist jedoch keine Grenze gesetzt. Dazu müsste entweder das Wurmloch entsprechend oft durchquert oder die Zeitdifferenz zwischen den Öffnungen vergrößert werden.
59Thorne, Kip: Gekrümmter Raum und verbogene Zeit. Lewis Thomas. Bd. 9 der Reihe: The Common-wealth Fund Book Program. - München:(Droemer Knaur) 1994; S. 574
3.2.3. Paradoxien
Beim Untersuchen möglicher Folgen von Zeitreisen in die Vergangenheit stößt man unweigerlich auf Widersprüche in der Logik, auf sogenannte Paradoxien. Da sie nur teilweise ein physikalisches Problem sind, sondern vor allem auch eine philosophische Frage, wird hier nicht explizit darauf eingegangen. Die Grundgedanken dieser Paradoxien, sowie einige Lösungsansätze werden jedoch im Anhang XII kurz dargestellt.
4. Schlussbewertung
Bei aufmerksamer Lektüre stellt man fest, dass es bislang kein physikalisches Gesetz gibt, welches Warp-Antrieb, Wurmlöcher und Zeitreisen im Allgemeinen verbietet. Das ist für die Science Fiction "die gute Nachricht nach zwanzig Jahren harter Forschungsarbeit"60 . Jedoch erscheint es äußerst fragwürdig, ob man die Realisierung von Raumzeit-Reisen in umfangreich nutzbarem Maß technisch bewältigen kann.
Mit unterlichtschneller Bewegung ist die Reichweite von Raumflügen sehr begrenzt. Es dauert gegenwärtig zu lange, die Entfernungen zwischen galaktischen Objekten zurückzulegen. Auch der Treibstoffverbrauch erscheint, selbst im effizientesten Fall - dem Antimaterie-Antrieb - zu groß, um Anwendung zu finden. Vor allem die relativistische Massenzunahme verhindert es, akzeptable Geschwindigkeiten zu erreichen.
Auch Zeitreisen in die Zukunft durch Zeitdilatation können kaum praktikabel werden, da die relative Geschwindigkeit des Zeitreisenden nahe der Lichtgeschwindigkeit sein muss, um einen annehmbar großen Dehnungsfaktor der Zeit zu erreichen.
Für Warp-Antrieb und Wurmlöcher ist die schlechte Nachricht, "dass sie, wenn sie überhaupt existieren, riesige Mengen an negativer Energie brauchen, damit sie"61 für Raumfahrzeuge nutzbar werden. Bisher wurden nur geringste Mengen negativer Energie gemessen. Es sind also vor allem energetische Probleme, die Raumzeit-Reisen zweifelhaft erscheinen lassen. "Bis wir eine Theorie der Quantengravitation haben, lässt sich vermutlich keine endgültige Antwort auf die Frage nach der Möglichkeit" von überlichtschnellen Reisen geben. Auch wenn sich irgendwann herausstellen wird, dass Warp-Antrieb und Wurmlöcher völlig unphysikalische Illusionen sind, sehen viele Physiker deren Erforschung jedoch nicht als umsonst an. Extreme hypothetische Gedankenkonstrukte wie Wurmlöcher oder Warp-Antrieb sind hilfreich, "mögliche Randbedingungen der Allgemeinen Relativitätstheorie auszuloten und Effekte einer künftigen Theorie der Quantengravitation zu erschließen"63 . Nur wenn wir uns unerforschten Gebieten der Physik zuwenden, können neue Zusammenhänge entdeckt werden, die den wissenschaftlichen Fortschritt gewährleisten.
- Stephen W. Hawking, Professor für Physik und Mathematik - "Es geht darum, die unbekannten Möglichkeiten der Existenz zu kartografieren."65
- Q, omnipotentes Wesen -
61Vaas, Rüdiger: Tunnel durch Raum und Zeit. - Stuttgart:(Franckh-Kosmos Verlags-GmbH & Co. KG) 2005; S. 144
62Krauss, Lawrence M.: Die Physik von Star Trek. Wolfgang Jeschke. 6. Auflage. - München:(Wilhelm Heyne Verlag GmbH & Co. KG); S. 65
63Vaas, Rüdiger: Tunnel durch Raum und Zeit. - Stuttgart:(Franckh-Kosmos Verlags-GmbH & Co. KG) 2005; S. 133
64Krauss, Lawrence M.: Die Physik von Star Trek. Wolfgang Jeschke. 6. Auflage. - München:(Wilhelm Heyne Verlag GmbH & Co. KG); S. 10
65Vaas, Rüdiger: Tunnel durch Raum und Zeit. - Stuttgart:(Franckh-Kosmos Verlags-GmbH & Co. KG) 2005; S. 161
5. Quellenverzeichnis
Literatur:
- Asimov, Isaac: Foundation. 3. Auflage. Band 06/8209 der Reihe: Heyne Science Ficti-on & Fantasy - München:(Wilhelm Heyne Verlag GmbH & Co. KG) 2000
- Davies, Paul: So baut man eine Zeitmaschine. Eine Gebrauchsanweisung. - Mün-chen:(Piper Verlag GmbH)
- Hawking, Stephen: Eine kurze Geschichte der Zeit. 19. Auflage. - Hamburg:(Rowohlt Taschenbuch Verlag GmbH) 2000
- Krauss, Lawrence M.: Jenseits von Star Trek. Die Physik hinter den Ideen der Science Fiction. Wolfgang Jeschke. - München:(Wilhelm Heyne Verlag GmbH & Co KG)
- Krauss, Lawrence M.: Die Physik von Star Trek. Wolfgang Jeschke. 6. Auflage. - München:(Wilhelm Heyne Verlag GmbH & Co. KG)
- Sagan, Carl: Contact. - München:(Droemersche Verlagsanstalt Th. Knaur Nachf.) 1997
- Thorne, Kip: Gekrümmter Raum und verbogene Zeit. Lewis Thomas. Band 9 der Reihe: The Commonwealth Fund Book Program. - München:(Droemer Knaur) 1994
- Vaas, Rüdiger: Tunnel durch Raum und Zeit. - Stuttgart:(Franckh-Kosmos Verlags-GmbH & Co. KG) 2005
- Wells, Herbert G.: Die Zeitmaschine. - Zürich:(Diogenes Verlag AG) 1947
Film:
- Roddenberry, Gene und Rick Berman: Star Trek. Fernsehserie und Spielfilme. Paramount Pictures. - San Francisco 1966-2005
Software:
- Interaktive Naturwissenschaften 2003. Version XIII. © Polster, Steffen. 1993/2003
Internet:
- http://abenteuer-universum.de/merkur.html#rot (22.01.2006)
- http://de.wikipedia.org/wiki/Michelson_Morley (14.01.2006)
- http://de.wikipedia.org/wiki/M%C3%B6%C3%9Fbauer-Effekt (03.01.2006)
- http://de.wikipedia.org/wiki/Periheldrehung (22.01.2006)
- http://de.wikipedia.org/wiki/Robert_Pound (03.01.2006)
- http://de.wikipedia.org/wiki/Universum_%28Astronomie%29 (03.01.2006)
- http://de.wikipedia.org/wiki/Zeitdilatation (03.01.2006)
- http://www.physik.uni-muenchen.de/leifiphysik/web_ph12/versuche/09photmasse/photmasse.htm (03.01.2006)
6. Anhang
6.1. Anhang I
Eine Hauptaussage der Speziellen Relativitätstheorie besteht in der sogenannten Längenkontraktion: Die Länge eines Objektes ist eine relative Größe, das heißt sie hängt von der Geschwindigkeit des Beobachters in Bezug auf das Objekt ab. Quantitativ drückt sich das Phänomen der Längenkontraktion in der Formel

aus. Bewegt sich ein Maßstab der (im relativ zu ihm ruhenden Bezugssystem gemessenen) Länge l' relativ zum Beobachter B mit konstanter Geschwindigkeit v, so nimmt B in seinem Bezugssystem den Stab um den Faktor  verkürzt wahr. Ist beispielsweise l' = 2,00 m und die relative Geschwindigkeit zwischen den beiden Objekten v = 0,87 c = 2,61·108 m/s, so erscheint der Stab dem Beobachter nur rund
verkürzt wahr. Ist beispielsweise l' = 2,00 m und die relative Geschwindigkeit zwischen den beiden Objekten v = 0,87 c = 2,61·108 m/s, so erscheint der Stab dem Beobachter nur rund  lang, da
lang, da  ist. Aus dem Prinzip der Relativität folgt überdies, dass der Beobachter selbst im System des Maßstabes ebenso um den Faktor
ist. Aus dem Prinzip der Relativität folgt überdies, dass der Beobachter selbst im System des Maßstabes ebenso um den Faktor  kontrahiert erscheint.
kontrahiert erscheint.
6.2. Anhang II

Graph der Funktion  , die den Faktor
, die den Faktor  der relativistischen Massenzunahme ( 1. ) sowie der Zeitdilatation ( 2. ) darstellt.66
der relativistischen Massenzunahme ( 1. ) sowie der Zeitdilatation ( 2. ) darstellt.66  steht für den Bruchteil der Geschwindigkeit v von der Lichtgeschwindigkeit c, mit der das Objekt bewegt wird. Der Funktionswert y ist der Faktor, mit dem...
steht für den Bruchteil der Geschwindigkeit v von der Lichtgeschwindigkeit c, mit der das Objekt bewegt wird. Der Funktionswert y ist der Faktor, mit dem...
- die Ruhemasse m0 des Objektes multipliziert wird, um die geschwindigkeitsabhängige relativistische Masse m(v) zu erhalten.
- das Zeitintervall Δt', also die von einem zu dem Objekt ruhenden Bezugssystem gemessene Dauer eines Vorgangs, multipliziert wird, um das Zeitintervall Δt, also die von einem zu dem Objekt mit der Geschwindigkeit v bewegten Bezugssystem gemessene Dauer eines Vorgangs, zu erhalten.
Da der Funktionsgraph erst für x >0,1 merklich von y = 1 abweicht, ist verständlich, dass relativistische Berechnungen erst für größere x-Werte notwendig sind.
66erstellt mit: Interaktive Naturwissenschaften 2003. Version XIII. © Polster, Steffen. 1993/2003
6.3. Anhang III

Stark übertriebene Darstellung der Merkurbahn während drei Umläufen um die Sonne.67 Tatsächlich ist die elliptische Bahn nicht derart ausgeprägt. Der sonnennächste Punkt, das Perihel, wandert pro Sonnenumrundung lediglich um 1,38 Bogensekunden.
67aus http://de.wikipedia.org/wiki/Periheldrehung (22.01.2006)
6.4. Anhang IV

Veranschaulichung des Gezeiteneffekts. Die Pfeile stehen für die Kraftvektoren, die an den verschiedenen Körperteilen angreifen. Links (Bezugssystem Planet): Alle Kräftevektoren zeigen in Richtung Massenschwerpunkt (= gravitationsausübendes Zentrum) und sind umso länger, je näher sie ihm sind. Das heißt, die Körperteile bewegen sich entlang geodätischer Linien durch die gekrümmte Raumzeit. Subtrahiert man links den mittleren Kraftvektor von jedem anderen Kraftvektor, so erhält man die Kraftvektoren die der Astronaut spürt (= Rechts (Bezugssystem Astronaut)). Er wird seitlich komprimiert und in der Länge gestreckt. Denkt man sich einen Planeten mit Wasseroberfläche anstatt des Astronauten, so erfährt das Gewässer ebenfalls eine seitliche Kompression (hier herrscht Ebbe) und eine Dehnung in Längsrichtung (hier herrscht Flut).
68nach Thorne, Kip: Gekrümmter Raum und verbogene Zeit. Lewis Thomas. Bd. 9 der Reihe: The Commonwealth Fund Book Program. - München:(Droemer Knaur) 1994; S. 117
6.5. Anhang V
Seit 1915 machten sich viele Physiker an die Auswertung der Speziellen und Allgemeinen Relativitätstheorie, arbeiteten neue Vorhersagen heraus und schufen eine neue Kosmologie. So auch der britische Physiker Paul Adrien Maurice Dirac, der in den 20er Jahren die Spezielle Relativitätstheorie auf sehr kleinem Maßstab auswertete. Er versuchte das Verhalten von Elektronen zu beschreiben. In solch kleinen Maßstäben gelten jedoch die Gesetze der Quantenmechanik, die die Wechselwirkungen von Teilchen im atomaren Bereich beschreibt. Um sie zu verstehen, sind ein neuer Blickwinkel auf den Kosmos sowie neue mathematische Hilfsmittel nötig. Dirac gelang es 1928, die Dirac-Gleichung zu erstellen, die "das relativistische Verhalten von Elektronen unter vollen quantenmechanischen Bedingungen"69 beschreibt. Dazu musste jedoch ein neues, bisher unbekanntes Elementarteilchen mit seltsamen Eigenschaften postuliert werden, dessen Existenz vier Jahre lang im Dunkeln blieb. 1932 entdeckte man in der kosmischen Strahlung jedoch genau dieses hypothetische Teilchen. Es hatte exakt die gleiche Masse wie das Elektron, jedoch eine positive Elementarladung, und wurde fortan als Antielektron oder Positron bekannt. Nun lag es auf der Hand, dass zu jedem Materieteilchen ein Antimaterieteilchen existiert, das stets die gleiche Masse hat, jedoch, sofern vorhanden, entgegengesetzte elektrische Ladung.
Das wichtigste Charakteristikum von Antimaterie ist jedoch folgendes: Wenn Antimaterie auf Materie trifft, dann annihilieren sich beide vollständig zu elektromagnetischer Strahlung typischer Frequenz f oder, gemäß dem Welle-Teilchen-Dualismus anders ausgedrückt, zu Photonen, deren Energie mit E = h · f ausgedrückt wird, wobei h= 6,63 · 10-34 Js das Plancksche Wirkungsquantum ist. Die Energiemenge E, die dabei freigesetzt wird, ist die Energie der kompletten Massen m(v) von Teilchen und Antiteilchen und lässt sich folglich gemäß der Speziellen Relativitätstheorie mit E = 2m(v) · c2 berechnen. Ist der Gesamtimpuls des Systems 'Teilchen-Antiteilchen' gleich null, so entstehen zwei Photonen, die sich in entgegengesetzter Richtung voneinander entfernen, sodass deren Gesamtimpuls in Übereinstimmung mit dem Impulserhaltungssatz ebenfalls null ist. Die Energie eines Photons beträgt in diesem Fall E = h · f = m(v) · c2.
Diese in der Masse der (Anti-)Teilchen gespeicherte immense Energiemenge wird also immer dann freigesetzt, wenn Antimaterie mit Materie zusammentrifft, und stellt deswegen ein Lagerungsproblem der Antimaterie dar, da sich jegliche Behältnisse mit der gelagerten Antimaterie annihilieren würden. Elektrisch geladene Antiteilchen lassen sich relativ leicht durch ein magnetisches Feld aufbewahren. Bewegen sich die geladenen Antiteilchen mit bestimmter Geschwindigkeit in einem Feld bekannter magnetischer Flussdichte, so bewegen sie sich auf einer Kreisbahn mit berechenbarem Radius70 und können dadurch festgehalten werden. Antiatome, die wie "normale" Atome auch nach außen elektrisch ungeladen sind, können durch Ausnutzung einer Eigenschaft des Spins ebenfalls durch starke magnetische Felder festgehalten werden, jedoch nur bei Abkühlung auf Temperaturen, die knapp über dem absoluten Nullpunkt (0 K) liegen. Dieses Verfahren erscheint zunächst komplizierter als das Festhalten geladener Antiteilchen. Doch bei großen Mengen würde der energetische Aufwand zur Speicherung der geladenen Antiteilchen viel größer, da diese durch ihre Abstoßung eine enorme Kraft hervorriefen, die wiederum durch extrem starke Magnetfelder kompensiert werden müsste.
Bisher wurde noch kein Anzeichen dafür entdeckt, dass sich Antimaterie anders in Bezug auf physikalische Gesetze verhält als Materie. Dies führt jedoch zu einem noch nicht restlos erklärten Problem: Unser Universum besteht - bis auf einige extrem kurzlebige Antimaterieteilchen in der kosmischen Strahlung und einige in Teilchenbeschleunigern künstlich hergestellte Antimaterieteilchen - nur aus Materie. Nach der Entstehung des Universums im Urknall müssen sich jedoch beide Arten von Materie gebildet haben. Ursprünglich gab es viel mehr Materie und Antimaterie als heute, die sich kurz darauf jedoch wieder gegenseitig annihilierten. Da es aber heute noch Materie gibt, muss etwas mehr Materie als Antimaterie nach dem Urknall existiert haben. Das Verhältnis lässt sich aus der kosmischen Hintergrundstrahlung errechnen, die in der Zeit kurz nach dem Urknall entstand, als sich Materie und Antimaterie annihilierten. Wenn die physikalischen Gesetze aber keine Präferenz für Materie oder für Antimaterie haben, warum entstand dann kurz nach dem Urknall eine Asymmetrie zugunsten der Materie?
70vgl. Krauss, Lawrence M.: Die Physik von Star Trek. Wolfgang Jeschke. 6. Auflage. - München:(Wilhelm Heyne Verlag GmbH & Co. KG); S. 101
6.6. Anhang VI
Legt das Raumschiff mit der idealisierten Geschwindigkeit  2,997· 108 m/s die Strecke
2,997· 108 m/s die Strecke  von der Erde zum Polarstern zurück, so kommt es dort, im Zeitmaß der Erde, nach der Zeit Δt = Δs/v =
von der Erde zum Polarstern zurück, so kommt es dort, im Zeitmaß der Erde, nach der Zeit Δt = Δs/v = 
an. Für die Raumschiffbesatzung dauert der Flug gemäß Formel I nur die Zeit  .
.
6.7. Anhang VII

Zweidimensionale Darstellung von drei Universen (= Ebenen) von denen je zwei durch Wurmlöcher (a, b) verbunden werden.71 Ein weiteres Wurmloch (c) verbindet zwei Regionen innerhalb eines Universums, wobei in der Realität die räumliche Distanz zwischen den beiden Öffnungen durch das Wurmloch (das heißt durch die Röhre) durchaus kleiner sein kann als durch den 'normalen' Raum (das heißt auf der nahezu flachen Ebene).
71nach Vaas, Rüdiger: Tunnel durch Raum und Zeit. - Stuttgart:(Franckh-Kosmos Verlags-GmbH & Co. KG) 2005; S. 137
6.8. Anhang VIII
Erstmals stieß der österreichische Physiker Ludwig Flamm 1916 auf solche Verbindungen zweier Orte der Raumzeit, als er die von dem deutschen Astronomen Karl Schwarzschild entdeckten, auf Schwarze Löcher hinauslaufenden Ergebnisse der allgemeinen Relativitätstheorie auf die Geometrie des Raumes hin genauer untersuchte. In den 30er Jahren kamen Einstein und sein amerikanisch-israelischer Mitarbeiter Nathan Rosen darauf zurück und berechneten, dass zwischen zwei Schwarzen Löchern tatsächlich eine tunnelartige Verbindung bestehen kann, die zwei verschiedene Universen verbindet. Diese Einstein-Rosen-Brücken haben die oben allgemein für Wurmlöcher beschriebene Gestalt, sind jedoch extrem instabil, sodass "nichts (weder Menschen noch Strahlung, noch Signale irgendwelcher Art) von einem Ende zum anderen gelangen kann."72 Außerdem wären Schwarze Löcher völlig ungeeignet zum Durchqueren von Einstein-Rosen-Brücken, da die Gezeitenkräfte jegliche Objekte zerreißen und seitlich zerquetschen würden. Zudem würde einfallende kosmische Strahlung durch die Raumzeit-Krümmung noch energiereicher werden, da sie eine höhere Frequenz erhält. Dies wäre ebenfalls tödlich für Raumfahrer, die ferner unweigerlich an der Singularität zerschellen würden, also an dem Punkt, an dem die gesamte Masse des Schwarzen Loches konzentriert ist. Dieses Problem könnte mit einem sogenannten Kerr-Tunnel vermieden werden. Der neuseeländische Mathematiker Roy Kerr untersuchte 1963 rotierende Schwarze Löcher, die vermutlich den größten Teil aller Schwarzen Löcher ausmachen, da Schwarze Löcher aus massereichen Sternen entstehen, die gewöhnlich einen Drehimpuls haben. Die dadurch hervorgerufene Zentrifugalkraft wirkt also der Gravitation entgegen, was dazu führt, dass rotierende Schwarze Löcher eine ringförmige Singularität haben, keine punktförmige, wie statische Schwarze Löcher. Man könnte also über die Polregion und durch die ringförmige Singularität das Schwarze Loch durchfliegen und durch den Kerr-Tunnel in einem anderen Universum ankommen. Das andere Ende des Tunnels liegt jedoch ebenfalls hinter dem Ereignishorizont eines Schwarzen Loches verborgen, also hinter der Grenze, an der die Raumzeit-Krümmung so stark ist, dass die Fallbeschleunigung gleich der Lichtgeschwindigkeit pro Sekunde ist und somit nichts sie von innen nach außen überwinden kann. Dadurch wäre der Raumfahrer hinter dem Ereignishorizont gefangen, er könnte zwar den Kerr-Tunnel beliebig oft durchqueren, jedoch nie einen der beiden Ereignishorizonte überschreiten und in das umgebende Universum eintreten. Einen Ausweg daraus boten die hypothetischen Weißen Löcher, die als Gegenstück von Schwarzen Löchern stets Energie und Materie emittierten und nichts ihren Antihorizont von außen nach innen überqueren könnte. Sie könnten als Ausgang eines Kerr-Tunnels dienen, über den sie mit einem Schwarzen Loch verbunden wären. Es hat sich jedoch herausgestellt, dass Weiße Löcher sehr instabil wären, denn schon nach Bruchteilen von Sekunden hätte sich dermaßen viel Materie und Energie um sie herum angesammelt, dass sie sofort zu Schwarzen Löchern umgewandelt würden. Es zeigt sich also, dass Wurmlöcher zwischen Schwarzen Löchern, wenn sie überhaupt existieren können, keine Option für Raumzeit-Reisen darstellen.
72Thorne, Kip: Gekrümmter Raum und verbogene Zeit. Lewis Thomas. Bd. 9 der Reihe: The Commonwealth Fund Book Program. - München:(Droemer Knaur) 1994; S. 555f
6.9. Anhang IX

Veranschaulichung des Quantenschaums in einem zweidimensionalen Universum, bei dem die Krümmung in die dritte Dimension eingebettet ist.73 Die Raumzeit ist von einer Vielzahl virtueller Wurmlöcher durchsetzt, die mit einer bestimmten Wahrscheinlichkeit für extrem kurze Zeit entstehen und wieder verschwinden.
73nach Thorne, Kip: Gekrümmter Raum und verbogene Zeit. Lewis Thomas. Bd. 9 der Reihe: The Com-monwealth Fund Book Program. - München:(Droemer Knaur) 1994; S. 565
6.10. Anhang X
Bewegt man sich mit einer Geschwindigkeit von v = 0,999999999·c relativ zu einem Objekt für die Flugzeit Δt' = 8d , so ist auf dem Objekt gemäß Formel I bereits die Zeit  vergangen.
vergangen.
6.11. Anhang XI
Gemäß Formel I ergibt sich für die Zeit Δt, die von außen betrachtet in der stationären Wurmloch-Öffnung verstreicht, bei einer relativen Bewegung der anderen Öffnung mit der Geschwindigkeit v =0,999996246 · c und der Bewegungsdauer Δt = 24h = 1d:

6.12. Anhang XII
Bisher ungelöste Probleme, die bei Zeitreisen in die Vergangenheit auftreten, bestehen in Paradoxien, also in Widersprüchen in der Logik. Dabei wird grundsätzlich zwischen zwei verschiedenen Paradoxien unterschieden:
- Die bekanntesten Widersprüche "werden als Konsistenz-Paradoxien bezeichnet"74 , sind jedoch vor allem auch als 'Großvater-Paradoxon' oder 'Muttermord-Paradoxon' bekannt. Sie lauten folgendermaßen: Ein Zeitreisender reist in die Vergangenheit und tötet einen seiner Vorfahren, zum Beispiel seinen Großvater, ehe dieser des Zeitreisendens Großmutter schwängern konnte. Somit konnte das eine Elternteil niemals geboren werden, wodurch auch der Zeitreisende niemals geboren werden konnte. Wenn dieser aber niemals geboren wurde, konnte er auch nicht in die Vergangenheit reisen und seinen Großvater töten. Wenn dieser aber nicht getötet wird, dann lebt er doch, und damit lebt auch der Zeitreisende, der also doch die Zeitreise durchführen und seinen Großvater Großvater töten kann. Dies kommt nie zu einem Ende und man weiß nicht, was nun Wirklichkeit ist. Dieses 'Konsistenz-Paradoxon' ist ein Widerspruch, da es das Gefüge von Ursache und Wirkung zerstört, ein Fundament der Physik und der Logik. Gewöhnlich folgt eine Wirkung immer einer Ursache. Die Ursache beeinflusst also stets die Wirkung, aber nie umgekehrt. Hier verhindert die Wirkung (also die Existenz des gewalttätigen Zeitreisenden) ihre eigene Ursache (die Existenz des Großvaters), was dazu führt, dass die Wirkung gar nicht erst entsteht und so weiter.
- Des Weiteren gibt es die sogenannten "Bootstrap-Paradoxien - nach der Redewendung ,sich an den eigenen Schuhriemen herausholen'"75 . Angenommen ein Student hat den Beweis für ein wichtiges physikalisches Gesetz aus einem alten Lehrbuch einer Bibliothek, wobei das Gesetz ursprünglich von einem bestimmten Professor bewiesen wurde. Nun reist der Student in der Zeit zurück und übergibt dem Professor den Beweis, bevor dieser selbst das Gesetz bewiesen hat. Da der Professor den Beweis nun hat, veröffentlicht er ihn in einem Buch, das der Student Jahre später findet. Der Beweis befindet sich nun in einer 'Kausalen Schleife', das heißt er wird nie richtig bewiesen, er hat also nie einen richtigen Anfang. Dies kommt dadurch zustande, dass die Wirkung (also das Buch mit dem Beweis in der Bibliothek) zu ihrer eigenen Ursache (Professor veröffentlicht den Beweis) wird. Beide Paradoxien zerstören also das Kausalitätsprinzip, wonach die Ursache der Wirkung stets vorausgeht. Darauf beruhen jedoch alle Naturgesetze. So musste man Lösungen entwickeln, die paradoxe Situationen vermeiden:
- Einige Wissenschaftler sind der Überzeugung, dass man physikalische Gesetze entdecken wird, die alle Phänomene, die Zeitreisen ermöglichen, grundsätzlich ausschließen. Damit wären auch alle Paradoxien beseitigt, da diese nur durch Zeitreisen zustande kommen.
- Nicht ganz so konservativ ist die 'Chronology Protection Conjecture' (Vermutung zum Schutz der Zeitordnung) von Stephen Hawking, wonach physikalische Gesetze verhindern, "daß makroskopische Körper Information in die Vergangenheit tragen können."76 . Es sind also keine Zeitreisen in die Vergangenheit möglich, bei denen diese beeinflusst wird. Dies heißt jedoch nicht, dass es keine Wurmlöcher gibt. Sie müssen lediglich so beschaffen sein, dass sie sich nicht für Informationstransfers in die Vergangenheit nutzen lassen. Zeitreisen in die Vergangenheit werden also nicht grundsätzlich ausgeschlossen. Sie sind zum Beispiel noch immer in Gödels rotierendem Universum möglich oder in Schwarzen Löchern, verborgen hinter dem Ereignishorizont.
- Eine weitere Möglichkeit, paradoxe Situationen zu vermeiden, besteht im sogenannten 'Selbstkonsistenzprinzip', demzufolge man zwar die Vergangenheit beeinflussen, sie aber nicht ändern kann. Es könnte zum Beispiel möglich, eventuell sogar nötig sein, in die Vergangenheit zu reisen und seine Großeltern zu einem Rendezvous zu bringen um so letztendlich die eigene Existenz sicherzustellen. Es ist aber nicht möglich, sie zu ändern, also den Großvater zu töten. Es wird garantiert etwas dazwischen kommen um den Mord zu verhindern; der Zeitreisende verfehlt beispielsweise sein Opfer oder er wird unerwartet von Mitleid überfallen. Es wird also nicht funktionieren, die Vergangenheit zu verändern, weil sie bereits auf eine bestimmte Weise determiniert ist
- Paradoxien kann man auch lösen, indem man mit der sogenannten 'Viele-Welten-Hypothese' der Quantenmechanik argumentiert. Gemäß der Quantenmechanik hängt es nur vom Zufall ab, ob Ereignisse im atomaren Bereich geschehen oder nicht, ob zum Beispiel ein radioaktives Atom zu einem bestimmten Zeitpunkt zerfällt oder nicht. Die 'Viele-Welten-Hypothese' sagt nun aus, dass bei jeder zufälligen Entscheidung zwischen zwei Zuständen nicht nur einer realisiert wird, sondern dass sich das Universum in beliebig viele Paralleluniversen aufspaltet. So kann jeder Zustand in einem Universum realisiert werden. Am Beispiel des radioaktiven Atoms bedeutet dies, dass es ein Universum gibt, in dem das Atom zu einem bestimmten Zeitpunkt zerfallen ist, und dass es ein anderes Universum gibt, in dem das Atom zu diesem Zeitpunkt nicht zerfallen ist. Nun kann man annehmen, dass jede Zeitreise in die Vergangenheit nicht nur in eine andere Zeit führt, sondern dass durch die 'Viele-Welten-Hypothese' ein neues Paralleluniversum entsteht, in das der Zeitreisende gelangt. Er verschwindet also aus seinem Universum und gerät in ein Paralleluniversum, in dem bis auf das Ereignis 'Zeitreise' alles vollkommen gleich ist. Am Beispiel des 'Konsistenz-Paradoxons' bedeutet es, dass der Zeitreisende seinen Großvater töten kann, weil er den Großvater in einem Paralleluniversum tötet. Dies führt jedoch nicht zu des Zeitreisenden Verschwinden, da er aus einem anderen Universum stammt. Dafür verschwinden jetzt alle Nachfahren des getöteten Großvaters in dem Universum, in dem der Zeitreisende ankam. Dies führt nun aber zu keinem Paradoxon, da der Doppelgänger des gewalttätigen Zeitreisenden nicht am Mord beteiligt ist.
Falls die 'Viele-Welten-Hypothese' zutrifft, müsste jedoch die Physik, insbesondere die Erhaltungssätze, erweitert werden. Denn falls ein Zeitreisender tatsächlich in ein Paralleluniversum gelangt, fehlt seine Masse im ursprünglichen Universum, was ein Verstoß gegen den Energieerhaltungssatz wäre. - Ein ganz radikaler Lösungsweg besteht in der kompletten Neuformulierung der Physik und Logik. Wenn Zeitreisen in die Vergangenheit möglich sind, könnte es sein, dass das Kausalitätsprinzip erweitert werden müsste und damit alle geltenden Naturgesetze. Möglicherweise ist unser Verständnis von Ursache und Wirkung nur ein Spezialfall einer allgemeineren, allumfassenderen Ordnung, in der die Wirkung nicht immer eine Folge der Ursache ist. Sogenannte Paradoxien wären dann nur ein Irrtum, der durch den zu starren menschlichen Verstand entsteht.
75Vaas, Rüdiger: Tunnel durch Raum und Zeit. - Stuttgart:(Franckh-Kosmos Verlags-GmbH & Co. KG) 2005; S. 216
76Hawking, Stephen: Eine kurze Geschichte der Zeit. 19. Auflage. - Hamburg:(Rowohlt Taschenbuch Ver-lag GmbH) 2000; S. 211