Abenteuer-Universum

Ich warte gespannt auf deinen Beitrag zur Herleitung von p(v).

Was meinst du genau mit 'was bedeutet die Lorentztrafo....'?
Für Ort und Zeit heißt es eben, dass man x' ausrechnen kann, wenn man x kennt und umgekehrt. Und für t genau so.

Na ja, das ist schon noch etwas ungenau. Das gleiche könnte ich auch für die Galilei-Trf. sagen. Was sind denn die Unterschiede zur Galilei-Trf.? Was kann man bzgl. der Vierervektoren sagen? ...

Kleiner Tip:

Bei der Galileitransformation gilt
t' = t
und
x' = x'(x)
mit
d(x',y') = d(x,y)
wobei d den Abstand zweier Raumpunkte x und y bedeutet; x und y sind Dreier-Vektoren

Wieviele elementare Galileitransformationen bzw. welche "Typen" gibt es?
Wie sieht das bei der Lorentztranformation aus?

tomS hat geschrieben:Wieviele elementare Galileitransformationen gibt es?

Naja, wenn man ein bewegtes und ein unbewegtes System hat, dann ist x' = x - vt und andersrum eben x = x' + vt. Der Rest ist gleich.

Bei der Lorentztrafo hat man x' = (x-vt)∙γ und zusätzlich t' = (t-vx/c²)∙γ
(mit γ:=Lorentzfaktor).

Warte mal, warum shreibst du eigentlich x' = x'(x)? Das hängt doch bei der Galilei-Trafo auch von v ab.

Also mir ging es bei der Zählung der Transformationen um die Symmetriegruppe, also um die Lorentzgruppe. Dabei zähle ich t => t' und t' => t natürlich nicht separat. Ich will auf sowas raus wie das, was ich kürzlich zu den Symmetriegruppen geschrieben habe.

Spannend wird das natürlich erst dann, wenn x als Vektor betrachtet wird, denn dann hab ich ja Rotationen und "Boosts". Was kommt dann beim Vergleich der Dimensionen der Galilei- und der Lorentzgruppe heraus?

Warum schreibe ich x' = x'(x)? Weil ich hier die Abhängigkeit der neuen von den alten Koordinaten unterstreichen will. Natürlich geht auch v ein, aber als Parameter, nicht als Koordinate.

Das heißt, dass bei der Lorentztrafo auch x' = x'(x) ist. Okay, hab nur gedacht, du willst damit vielleicht aus was raus, weil ja das v bei der Lorentztrafo eine größere Rolle spielt.

Ach ja, ich hab gerade noch ein bisschen rumgerechnet, um rauszubekommen, dass der Abstand d bei der Lorentztrafo nicht invariant ist (ich hab die Punkte a und b genannt):
Galilei:
http://freenet-homepage.de/SRT_leicht_g ... lileid.gif
Lorentz:
http://freenet-homepage.de/SRT_leicht_g ... rentzd.gif

Ich bezieh' mich auf ein paar Dinge, die ich unter
viewtopic.php?t=800
geschrieben habe:

x' = (x-vt) bzw. x' = (x-vt)∙γ nenne ich Boost; aber im allgemeinen sind x und x dreidimensionale Vektoren und die Formeln dann komplizierter.

Bei der Galilei-Trf. betrachte ich Rotationen und Boosts in drei Dimensionen. Da ich drei Freiheitsgrade für die Definition von Rotationen habe, gibt es drei Drehwinkel. Achtung: dass die Anzahl der Drewinkel gleich der Anzahl der Raumdimensionen ist, ist ein Spezialfall für drei Dimensionen!!! Betrachte zwei Dimensionen - da gibt es nur eine mögliche Drehung in der Ebene.
Außerdem habe ich drei mögliche Boosts, nämlich einen je Raumrichtung (das gilt jetzt für beliebige Dimensionen).
Also ist die Dimension der Transformationsgruppe 3 + 3 = 6.
Dabei stehen Rotationen und Boosts unverbunden nebeneinander, d.h. sie haben mathematisch nichts miteinander zu tun.

Nun zur Lorentz-Transformation: ich betrachte wieder Rotationen und Boosts in drei Raumdimensionen. Die Rotationen sind wieder die üblichen (mathematisch: eine Untergruppe), die Boosts mischen jetzt jedoch Raum und Zeit untrennbar miteinander! Betrachtet man zwei Boosts in unterschiedliche Richtungen hintereinander, so sind diese nicht mehr vertauschbar. Im Falle der Galilei-Transformation, kann ich jedoch problemlos zuerst in x und dann in y Richtung boosten - ist das selbe, wie wenn ich zuerst in y und dann in x-Richtung booste. Im Falle der Lorentztransformation enthält die Zusammengesetzte Transformation auch Rotationsanteile!
Die Dimension der Transformationsgruppe 3 + 3 = 6.

Mathematische Ursache ist, das die Lorentz-Transformation für N-dimensionale Raum-Zeit (üblicherweise N=4) aus der Gruppe SO(N-1, 1)
stammen. Diese hat eine Untergruppe SO(N-1), das ist die gewöhnliche Drehgruppe. Die restlichen Transformationen = die Boosts bilden jedoch keine Untergruppe.
Zur Dimension: In N Raum-Zeit Dimensionen, also für die Lorentzgruppe SO(N-1, 1), erhält man die Dimension D = N*(N-1)/2, die Drehgruppe SO(N-1) für die rein räumlichen Drehungen hat (N-1)*(N-2)/2. Berechnet man die Differenz, so findet man N-1, das ist die Anzahl der Boosts.

Zu d: man muss lediglich den richtigen Abstandsbegriff definieren.
Die SO(N-1, 1) lässt einen Abstand gemäß Pythagoras invariant, wobei in einer Koordinate (hier: die Zeit) das Vorzeichen umzudrehen ist. Der Abstand aus dem Pythagoras für die räumlichen Komponenten ist kein guter Begriff, da er nicht invariant unter Lorentztransformationen ist. Nur der Abstand d² = t² - x² ist invariant

Wie schaut's aus? Besteht noch Interesse an dem Frage-Antwort-Spiel?

Ich stell mal eine neue Frage zur Diskussion:

Was bedeutet der relativistische Pythagoras E² = p² + m² ?

Es besteht noch Interesse.

Gute Frage.
Schwer, im Netz dazu was zu finden, die Gleichung wird überall nur kurz am Rande erwähnt.
Sie setzt auf jeden Fall die relativistische Energie mit dem Impuls in Beziehung und findet in der Quantenphysik offenbar häufig Anwendung. Stichwörter, auf die ich gestoßen bin, wären Comptoneffekt und deBroglie-Wellenlänge.

Kleiner Hinweis:

Man kann ja für Zeit und Ort sogenannte Vierervektoren einführen, also



mit i=1,2,3

Dann definiert man das Skalarprodukt als



Für x² unterscheidet man die Fälle kleiner Null (raumartig), gleich Null (lichtartig) und größer Null (zeitartig). Das ist die Lichtkegelstruktur

x² ist die "invariante, vierdimensionale Länge", d.h. sie hat in allen Bezugssystemen die selbe Größe.

Man kann nun das selbe für Energie und Impuls tun - was passiert dann?

Okay, ich hab ein bisschen auf Al's Seite gespickt und bringe folgendes zusammen:

Wenn ich aus dem Impuls auch irgendwie einen Vierevektor machen will, nehme ich am besten Ruhemasse mal Vierergeschwindigkeit, also:




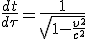
Mit erhält man:


und mit ein bisschen umformen schließlich:

Das heißt jetzt wohl, dass das Quadrat des Viererimpulses auch invariant ist.

Wenn wir jetzt an einem vorigen Punkt wieder einsteigen, können wir den relativistischen Pythagoras herleiten:
Man kann schreiben (mit dem dreidimensionalen Impuls p=mv):





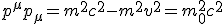
Oder mit c=1 deine Variante.
Oh Gott, hoffentlich war das richtig

Ja, das wir richtig

Es ist eigentlich von der Idee her ganz einfach: die Gruppe der Lorentztransformationen SO(1,3) ist eine Abart der vierdimensionalen Rotationsgruppe SO(4).

Die SO(4) lässt vierdimensionale Vektoren unter der üblichen Norm invariant, während man bei der Lorentzgruppe die spezielle Metrik g = diag(1, -1, -1, -1) betrachtet, d.h. die drei räumlichen Komponenten erscheinen mit einem Minuszeichen.

Während die normale Rotationsgruppen mit Drehwinkeln alpha, ... und sin / cos daherkommen, werden in der Lorentzgruppe die Drehungen "um die Zeitachse" mit imaginären Winkeln i*alpha eingeführt. Dadurch erhält man aus sin / cos jeweils sinh / cosh. Diese Drehunge heißen Boosts und beschreiben die Mischung von Raum und Zeit in der Lorentztransformation.

Die invariante Masse aus E² - p² = m² hat noch eine weitere interessante Bedeutung: Man nimmt an, dass ALLE in der Natur vorkommenden Symmetrien dazu führen, dass Elementarteilchen sich bezüglich dieser Symmetrien klassifizieren lassen:

viewtopic.php?t=800&start=0&postdays=0& ... highlight=

Jede Gruppe hat bestimmte Gruppeninvarianten und jedes Elementarteilchen muss sich bzgl. dieser Invarianten klassifizieren lassen. Der Operator E² - p² ist der sogenannte "erste Casimiroperator", d.h. die erste Gruppeninvariante der Lorentzgruppe. Dass die Lorentzsymmetrie eine exakte Symmetrie ist, erzwingt, dass jedes Elementarteilchen eine festen (unveränderlichen, d.h. invarianten) Wert für diese Gruppeninvariante hat.

Ich muss sagen, die Sache mit den Symmetriegruppen verwirrt mich trotz aller Erklärungen ein wenig, aber ich glaube, bei dem Versuch das komplett zu klären, würden wir ziemlich lange ziemlich weit vom Thema abkommtn.
Deswegen bitte ich lieber um die nächste Frage.

was verwirrt dich denn?

Das ist nur, weil ich so wenig über Symmetriegruppen weiß. Ich weiß nur, dass eine Gruppe eine Menge mit ein paar Zusatzbedingungen ist.
Was sind die Elemente einer Symmetriegruppe?
Wo ist bei den Lorentztransformationen ein imaginäer Winkel i alpha?
Wie beschreibt man überhaupt Symmetrien mit Matrizen?
Wofür braucht man bei der RT überhaupt den Begriff der Symmetriegruppe?

Das sind so die unmittelbaren Fragen, die ich gerade im Kopf hab, aber bei weitem nicht die einzigen.

Das sind ja schon einige (sehr interessante) Fragen.

Hilft das, was ich an andere Stelle geschrieben habe? viewtopic.php?t=800&start=0&postdays=0& ... highlight=

Ein wenig.
Es bleibt auf jeden Fall das mit dem imaginären Winkel und wo die Matrizen herkommen.
Sind die elemente der Gruppe nun die Lorentztrafos als Funktionen?

Okay, ich hab glaub das Gefühl, dass ich das mit der Symmetriegruppe jetzt nachvollziehen kann.

Das provoziert sofort die nächste Frage:

Wie transformieren sich ko- und kontravariante Vektoren sowie Tensoren unter der Lorentzgruppe?

Hast du das nicht da schon geschrieben?



Damit transformiert sich ein Vektor gemäß

Ich hab aber noch nix zu ko- und kontravariant geschrieben. Und auch noch nix zu Skalaren.

Die Gleichung ist sozusagen noch zu präzisieren :-)

Okay, wenn ich da mit Symmetriegruppen rangehen soll, hab ich erstmal keine Ahnung, aber bei ko- und kontravariant denke ich an Tensorrechnung.

Kann man etwas in der Art sagen:
Die Lorentztrafos sind ja eigentlich Transformationen zwischen Koordinaten und nicht zwischen Vektorkomponenten. Dann hätte man erstmal für die Koordinaten (wenn man als Matrix schreibt):


und für kontravariante Komponenten eines Vektors:



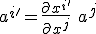
und ist doch wieder . Damit hätte man dann:



Es wäre ziemlich praktisch, wenn das annähernd richtig wäre, dann wäre nämlich .

Du verwendest die allgemeine Darstellung der Koordinatentransformation über die Differentiale - OK.

Grundsätzlich ist die Darstellung mit der Transformationsmatrix = einem Element der Lorentzgruppe genau richtig. Die Matrix enthält (gemischt) ko- und kontravariante Indizes, so dass die entsprechenden Vektoren mit dieser Matrix transformiert werden - OK.

Die Invertierung dieser Matrix, d.h. Rück- statt Hintransformation über hoch- und runterziehen der Indizes ist ebenfalls OK.

Generell sollten dann immer Indizes verwendet werden (meine Darstellung war schlampig). Außerdem sollte festgelegt werden, ob man griechische oder lateinische Indizes verwendet. Häufig steht i nur für die räumlichen Indizes 1..3. Ich verstehe deine Notation so, dass i=0..3 sein kann.

und wie sieht die Transformation von allgemeinen Tensoren mit mehreren Indizes aus?

Naja, das wird dann wohl einfach

sein.

Soll ich auch noch die ganzen gemischt ko- kontravarianten hinschreiben?