Seite 7 von 10
Verfasst: 10. Aug 2008, 08:07
von tomS
Wenn du die normalen Formeln der Lorentztranformation (mit v und den Wurzeln) nimmst und t² - x² = const. berechnest, dann spielt sowas wie cosh²x - sinh²x = 1 eine Rolle. x = x(v) und kann berechnet werden.
R kannst du je jetzt differenzieren und damit M berechnen.
Ist das Problem dann, wie du von M auf J und K kommst?
Verfasst: 10. Aug 2008, 16:48
von breaker
Sorry, aber wenn ich mit den normalen Lorentz-Trafos t²-x²=C ausrechne, krieg ich t'²-x'²=C (was wegen der Metrik und so ja eigentlich auch recht logisch ist). Aber v kürzt sich raus und cosh und sinh kommen nicht vor. Gibts da Gleichungen, die die mit Wurzeln verbinden?
Verfasst: 11. Aug 2008, 08:46
von tomS
Schreibe
t => γ(t+vx)
t => γ(x+vt)
γ² = 1/(1-v²)
Wenn du jetzt t² -x² berechnest, dann kürzt sich im wesentlichen (1-v²) weg.
Schreibe jetzt die Transformationsgleichung des Vektors (t,x) als Matrix, also
(t,x) => L*(t,x)
In der Matrix L hast du vier Terme, jeweils zweimal c(v) und s(v) von der Form
c = 1/γ
s = v/γ
Berechne
c² - s² =1/γ² - v²/γ² = (1-v²)/γ² = 1
Diese Beziehung gilt auch für cosh und sinh
Definiere nun
cosh η = 1/γ
sinh η = v/γ
Dann gilt
tanh η = v
η ist die sogenannte Rapidität. Der von mir erwähnte imaginäre Drehwinkel ist dann i*η.
Verfasst: 11. Aug 2008, 12:58
von breaker
Ah, stimmt. Jetzt passt alles wieder ein bisschen mehr zusammen.
Ich hab mal Spaßhalber J¹ ausgerechnet und ½(M³²-M²³) rausbekommen.
Wenn M antisymmetrisch ist, wäre das doch nur wieder M³². Wo steckt da der Sinn?
Verfasst: 11. Aug 2008, 15:37
von tomS
Es wird einfacher zu interpretieren, d.h. der Sinn steckt darin, dass man
- mit den J's die SO(3) Drehgruppe als echte Untergruppe der SO(3,1) wiederfindet
- man aus den J's und K's einfach die beiden Fundanmentaldarstellungen (Kap. 7) konstruieren kann
Kleiner Hinweis: man muss später ja die Exponentialdarstellung berechnen; das ist für die vierdimensionalen Matrizen J und K natürlich lästig. Als warm-up kann man das mal für die Paulimatrizen machen. Diese haben ja interessanterweise dieselben Vertauschungsrelationen (bis auf einen Faktor) wie die Generatoren J der SO(3). D.h. dass zwar die komplexe "Drehgruppe" SU(2) und die dreidimensionale Drehgruppe SO(3) unterschiedlich sind, dass die Algebra jedoch dieselbe ist. Man kann also mal mit den Paulimatrizen rumspielen und dabei einiges über Drehungen lernen:
Picken wir uns eine Paulimatrix heraus, z.B. die dritte, und skalieren wir sie mit 1/2. Das Gebilde nennen wir t. Dann berechen wir
U = exp{i a t}
mit einer rellen Zahl a.
Berechnet man die Taylorreihe der e-Funktion, so erhält man, t, t², t³ usw.
Nun ist jedoch t² = 1/4
Sortiert man nun die Taylorreihe nach Potenzen von t (es gibt nur t° = 1 und t, denn t² = 1/4 und t³ = t²* t = 1/4 * t), so erhält man zwei separate Potenzreihen, die eine mit einem Faktor 1 die andere mit einem Vorfaktor t. Aus diesen beiden Potenzreihen kann man die für cos und sin ableiten. Man erhält zuletzt eine SU(2) Drehmatrix.
Analog kann man dies auch für die drei- bzw. vierdimensionalen Darstellungen tun. So kann man z.B. aus ähnlichen Rechnungen für die J's die Matrixdarstellung der SO(3) ableiten.
Wenn man eine Exponentialfunktion mit mehreren Winkeln und Generatoren berechnen will, dann führt man die Vektoren a und t ein und berechnet
U = exp{i a t}
Dabei muss man in der Taylorreihe aufpassen, denn man erhält Potenzen von (a t) und darf die t's nun nicht einfach vertauschen. Man muss statt dessen das Produkt zweier t's mittels einer Summe aus Kommutator und Antikommutator schreiben, also gemäß
AB = ½ {A,B} + ½ [A,B] = ½(AB+BA + AB-BA) = ½ (2 AB).
Dafür kennt man nun die Regeln (Kap. 4.2.2). Als Ergebnis erhält man die allgemeinste Form der SU(2) Drehmatrix.
Analog könnte man nun auch für die drei- und vierdimensionalen Darstellungen mit J und K vorgehen; die explizite Rechnung ist jedoch wesentlich aufwendiger. Man benötigt sie auch nicht. Für eine Veranschaulichung um was es geht, reicht das zweidimensionale Bespiel aus.
Verfasst: 12. Aug 2008, 19:47
von tomS
Ich wollte nach der Reaktivierung von TeX nochmal auf eine frühere Fragestellung verweisen, die wir hier diskutieren.
Es geht um die Lorentz-Transformation L von Vierervektoren sowie um die zugehörige Transformation G(L) der Spinoren:

 \rightarrow \psi^\prime (x^\prime) = G(L) \psi(x) )
Verfasst: 12. Aug 2008, 20:06
von breaker
Wenn ich das richtig verstanden hab, dann gibt dein U dann das Lambda, bzw. das A aus Kapitel 7.
Also die Transformationsmatrix der Spinoren.
Mir ist gerade aufgefallen, dass ich gar nicht weiß, was das phi und das ny in Kapitel 7 sind. Sind das beides Winkel von so einer R-Matrix?
Verfasst: 13. Aug 2008, 23:17
von tomS
Ja!
Sorry für die Verwirrung. In einem Text schreibe ich U, weil es sich um eine SU(2) Trf. als Beispiel und zunächst ohne Bezug zum PDF handelt. Mein G(g) entspricht dem A bzw. Lambda aus Kapitel 7.
phi und ny sind die drei Dreh- bzw. drei Boostparameter. Es gibt drei Erzeugende J und K für Drehungen bzw. Boosts (siehe die Def. in 6.5 mit k,m,n = 1 ... 3). Drei Drehungen entsprechend der drei Drehachsen, drei Boosts entsprechend der drei Richtungen. Zu jeder Erzeugenden gehört auch ein Parameter.
D.h. in den Formeln für Lambda stehen phi, ny, sowie J, K für jeweils Dreiervektoren, phi*J und ny*K sind die jeweiligen Skalarprodukte:

Verfasst: 15. Aug 2008, 22:43
von tomS
Und, wie schaut's aus? war's das zu den Spinoren, oder sind da noch Fragen offen?
Verfasst: 16. Aug 2008, 15:48
von breaker
Eine nächste Frage wäre mir sehr recht.

Verfasst: 19. Aug 2008, 00:45
von tomS
Ein kleiner Ausblick auf die ART:
was ist die Bedeutung einer Geodäte? wie kann man aus der Definition die relativistischen Bewegungsgleichungen ableiten?
Verfasst: 19. Aug 2008, 11:31
von breaker
Eine Geodäte ist die kürzeste Verbindung zwischen zwei Punkten, die in einem gekrümmten Raum nicht unbedingt einer Gerade entspricht. Das Licht bewegt sich auf Geodäten. Die Geodätengleichung bekommt man über ein Variationsproblem, indem man eben das Minimum der Kurvenlänge zwischen zwei Punkten sucht.
Verfasst: 19. Aug 2008, 22:20
von tomS
wie lautet denn die Formel für die Kurvenlänge und die daraus ableitbare Geodätengleichung?
Verfasst: 20. Aug 2008, 11:28
von breaker
Die Formel für die Kurvenlänge ist

wobei der Punkt die Ableitung nach Lambda bezeichnet.
Die Geodätengleichung lautet dann

Verfasst: 20. Aug 2008, 23:36
von tomS
Korrekt.
Interessanterweise kann man diese Länge als Wirkung eines Teilchens der Masse m interpretieren:

Statt lambda schreibt auch oft tau; tau bezeichnet dabei die Eigenzeit des Teilches.
Das Interessante ist, dass sich in dieser Darstellung unmittelbar eine Koordinateninvarianz zeigt, denn die Wirkung S (= die Länge der Kurve C) ist vällig unabhängig von der Parametrierung der Kurve. Jeder andere Parameter entlang der Kurve tut's genauso. Die Eigenzeit ist dabei natürlich eine naheliegende Wahl.
Verfasst: 20. Aug 2008, 23:37
von tomS
Nächste Frage?
Die wäre: wie kann man zeigen, dass die bekannte Lorentzkraft, die ein elektrisch geladenes Teilchen in einem Magnetfeld erfährt, tatsächlich ein echt relativistischer Effekt ist?
Verfasst: 21. Aug 2008, 17:05
von breaker
Hm, schöner Effekt, kannte ich noch gar nicht.
Wenn sich ein Elektron prallel zu einem stromdurchflossenen Leiter bewegt, dann erscheint der Leiter aus Sicht des Elektrons verkürzt. Allerdings nicht die Elektronen im Leiter, dnn die bewegen sich ja auch. Also sind in einem bestimmten Volumen im Leiter immer mehr positiv geladene als negativ geladene Teilchen. Aus Sicht des Elektrons ist der Leiter positiv geladen und es wird angezogen.
Verfasst: 21. Aug 2008, 22:18
von tomS
nö, da bist du falsch unterwegs.
Lorentkraft bedeutet, dass bewegte Ladungen in einem Magnetfeld eine Kraft erfahren, die senkrecht auf der Bewegungsrichtung und der Magnetfeldrichtung steht.
Verfasst: 22. Aug 2008, 10:29
von breaker
Okay, die Erklärung von mir gilt nur für Elektromagneten...
Aber hat es denn allgemein mit Zeit- oder Raumdehnung zu tun?
Verfasst: 22. Aug 2008, 21:42
von tomS
Nein.
Du hast doch die Geodäte aus einem Wirkungsintegral abgeleitet. Man kann dieses Wirkungsintegral um die Kopplung des Teilchens an das el.-mag. Feld erweitern und wiederum die Bewegungsgleichungen ableiten. Dann fällt die LOrentzkraft mit ab.
Bevor du das tust, solltest du deine Geodätengleichung (vorherige Frage) für den Fall des flachen Raumes vereinfachen.
Verfasst: 24. Aug 2008, 00:33
von breaker
Ist dann die Kopplung ans elektrische Feld eine Nebenbedingung bei der Variationsrechnung und man muss es mit einem Lagrange'schen Multiplikator lösen?
Verfasst: 24. Aug 2008, 18:58
von AlTheKingBundy
Schau Dir mal die klassische Lagrangefunktion an, aus der sich die Lagrangegleichungen durch Variation (analog zu den Geodäten) ergeben.
Die Beiträge sind (bis auf Proportionalitätsfaktoren):
u_my u_ny g^myny: Vierergeschwindigkeitenquadrat mit Metriktensor
u_my A^my: Mit elektromagnetischen Viererpotential.
Daraus ergeben sich die vollständigen Bewegungsgleichungen für ein Teilchen im Gravitationsfeld inklusive elektromagnetischer Wechselwirkung. Schön zu sehen ist, wie die Gravitation ans Geschwindigkeitsquadrat koppelt und der Elektromagentismus nur an die einfache Vierergeschwindigkeit.
Verfasst: 26. Aug 2008, 14:11
von breaker
Wovon hängt A denn ab?
Nur von
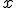
oder auch von

?
Verfasst: 26. Aug 2008, 14:26
von AlTheKingBundy
Das Viererpotential A (Indizes lasse ich jetzt weg, A = (A1, A2, A3, V), wobei V das Coulombpotential ist) hängt von den Viererkoordinaten ab (nicht von der Geschwindigkeit). Die Bewegungsgleichungen für das Viererpotentail resultieren aus den Maxwellgleichungen.
Quabla A = 0 im leeren Raum (Quabla = d^2/dx^2 + d^2/dy^2 + d^2/dz^2 - d^2/dt^2)
c = 1 gesetzt.
Mit der Lorentzeihung noch dazu:
dA1/dx + dA2/dy + dA3/dz + dV/dt = 0
Verfasst: 26. Aug 2008, 16:48
von breaker
Dann bekomme ich bei analoger Rechnung wie bei der Geodätengleichung (und falls ich richtig gerechnet habe) sowas:
=0)