Hinweis auf die DSGVO: Auf unserer Seite werden keine Dritt-Anbieter-Cookies verwendet und nur Daten erfasst, welche für das Minimum an Board-Funktionalität notwendig sind.
Bevor Sie sich registrieren oder das Board verwenden, lesen Sie bitte zusätzlich die DSGVO-Erklärung, welche in der Navigationsleiste verlinkt ist.
Kurzfassung der unserer Meinung nach wichtigsten DSGVO-Punkte:
Es kann vorkommen, dass Benutzer eigenverantwortlich Videos oder sonstige Medien in ihren Beiträgen verlinken, welche beim Aufruf der Forenseite als Teil der Seite samt zugehörigem Material mitgeladen werden. Sollten Sie dies nicht wünschen, verwenden Sie beim Benutzen des Forums einen Blocker wie z.B. uMatrix, welcher das Laden von Inhaltsblöcken von Fremd-URLs effektiv unterbinden kann.
Wir blenden keine Werbung ein und schränken die Inhalte in keinster Weise bei Benutzung von Addblockern ein. Dadurch ist die Grundfunktionalität des Forums auch bei vollständigem Blockieren von Drittanbieter-Inhalten stets gegeben.
Cookies werden unsererseits nur verwendet um das Einloggen des Benutzers für die Dauer der Forenbenutzung zu speichern. Es steht dem Benutzer frei die Option 'Angemeldet bleiben' zu verwenden, damit der Cookie dauerhaft gespeichert bleibt und beim nächsten Besuch kein erneutes Einloggen mehr notwendig ist.
EMail-Adressen werden für Kontakt bei wichtigen Mitteilungen und zur Widerherstellung des Passwortes verwendet. Die verwendeten IPs können von uns ohne externe Hilfsmittel mit keiner realen Person in Verbindung gebracht werden und werden nach spätestens 7 Tagen gelöscht. Diese IPs werden höchstens verwendet um Neuanmeldungen unerwünschter oder gesperrter Nutzer zu identfizieren und zu unterbinden. Wir behalten uns daher vor bei Verdacht, die Frist für die IP-Löschung auf maximal 14 Tage zu verlängern.
Unsere Webseite läuft auf einem virtuellen Linux-Server, welcher von einem externen Anbieter gehostet wird. Etwaige Verstöße der DSGVO-Auflagen seitens dieses deutschen Hosters können wir nicht feststellen und somit auch nicht verfolgen.
Wir halten Backups unserer Datenbanken, welche in regelmäßigen Abständen als Schutz vor Katastrophen, Hackerangriffen und sonstigen Ausfällen erstellt werden. Sollte ein Nutzer die Löschung seiner Daten wünschen, betrachten wir es als Unzumutbar die Backups auch von den Daten zu befreien, da es sich hierbei um eine mehrtägiges Unterfangen handelt - dies ist für eine Einzelperson beim Betrieb eines privaten Forums nicht zumutbar möglich ohne das Backup komplett zu löschen.
Sollten Sie etwas gegen die dauerhafte anonyme Speicherung ihrer EMail-Adresse, ihres Pseudonyms und ihrer Beiträge in einem Backup haben, sehen Sie von der Registrierung in diesem Forum ab. Für Mitglieder, welche vor dem 25.05.2018 registriert waren steht jedoch das Recht im Raum, eine Löschung der Datenbank-Backups zu beantragen.
Wenn dies Ihr erster Besuch hier ist, lesen Sie bitte zunächst die FAQs sowie die wesentlichen Regeln zur Benutzung des Forums.
Um an den Diskussionen teilnehmen zu können, müssen Sie sich zunächst registrieren.
Bevor Sie sich registrieren oder das Board verwenden, lesen Sie bitte zusätzlich die DSGVO-Erklärung, welche in der Navigationsleiste verlinkt ist.
Kurzfassung der unserer Meinung nach wichtigsten DSGVO-Punkte:
Es kann vorkommen, dass Benutzer eigenverantwortlich Videos oder sonstige Medien in ihren Beiträgen verlinken, welche beim Aufruf der Forenseite als Teil der Seite samt zugehörigem Material mitgeladen werden. Sollten Sie dies nicht wünschen, verwenden Sie beim Benutzen des Forums einen Blocker wie z.B. uMatrix, welcher das Laden von Inhaltsblöcken von Fremd-URLs effektiv unterbinden kann.
Wir blenden keine Werbung ein und schränken die Inhalte in keinster Weise bei Benutzung von Addblockern ein. Dadurch ist die Grundfunktionalität des Forums auch bei vollständigem Blockieren von Drittanbieter-Inhalten stets gegeben.
Cookies werden unsererseits nur verwendet um das Einloggen des Benutzers für die Dauer der Forenbenutzung zu speichern. Es steht dem Benutzer frei die Option 'Angemeldet bleiben' zu verwenden, damit der Cookie dauerhaft gespeichert bleibt und beim nächsten Besuch kein erneutes Einloggen mehr notwendig ist.
EMail-Adressen werden für Kontakt bei wichtigen Mitteilungen und zur Widerherstellung des Passwortes verwendet. Die verwendeten IPs können von uns ohne externe Hilfsmittel mit keiner realen Person in Verbindung gebracht werden und werden nach spätestens 7 Tagen gelöscht. Diese IPs werden höchstens verwendet um Neuanmeldungen unerwünschter oder gesperrter Nutzer zu identfizieren und zu unterbinden. Wir behalten uns daher vor bei Verdacht, die Frist für die IP-Löschung auf maximal 14 Tage zu verlängern.
Unsere Webseite läuft auf einem virtuellen Linux-Server, welcher von einem externen Anbieter gehostet wird. Etwaige Verstöße der DSGVO-Auflagen seitens dieses deutschen Hosters können wir nicht feststellen und somit auch nicht verfolgen.
Wir halten Backups unserer Datenbanken, welche in regelmäßigen Abständen als Schutz vor Katastrophen, Hackerangriffen und sonstigen Ausfällen erstellt werden. Sollte ein Nutzer die Löschung seiner Daten wünschen, betrachten wir es als Unzumutbar die Backups auch von den Daten zu befreien, da es sich hierbei um eine mehrtägiges Unterfangen handelt - dies ist für eine Einzelperson beim Betrieb eines privaten Forums nicht zumutbar möglich ohne das Backup komplett zu löschen.
Sollten Sie etwas gegen die dauerhafte anonyme Speicherung ihrer EMail-Adresse, ihres Pseudonyms und ihrer Beiträge in einem Backup haben, sehen Sie von der Registrierung in diesem Forum ab. Für Mitglieder, welche vor dem 25.05.2018 registriert waren steht jedoch das Recht im Raum, eine Löschung der Datenbank-Backups zu beantragen.
Wenn dies Ihr erster Besuch hier ist, lesen Sie bitte zunächst die FAQs sowie die wesentlichen Regeln zur Benutzung des Forums.
Um an den Diskussionen teilnehmen zu können, müssen Sie sich zunächst registrieren.
Rolle des Zufalls in der Physik:"Nebenrechnungen"
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
Selbst wenn das stimmen würde, erklärt es doch nicht von hier beobachteten Merkwürdigkeiten und Strukturen
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
Zunächst möchte ich noch einmal sagen, dass ich es besser fände, wenn wir hier nicht in Wahrscheinlichkeiten denken würden, sondern in Häufigkeiten bestimmter Ziffern oder Strukturen bei bestimmten betrachteten Mengengrößen. Diese Häufigkeiten sind einfacher zu erfassen und sind die Ursache für nicht-homogene Wahrscheinlichkeiten, wenn sie selbst nicht-homogen sind.
Die Ziffern haben mit den Zahlen erst einmal wenig zu tun.
Ich könnte auch im Dreiersystem rechnen und dann fragen, ob bestimmte, definierbare Ziffernfolgen öfter als andere vorkommen. Das ist dann der Fall, wenn ich zum richtigen Zeitpunkt aufhöre zu Zählen.
Ich sage es noch einmal:
Das Grundproblem scheint mir zu sein, dass die Methode "Grenzwertbetrachtung" streng genommen ungenügend ist, wenn es keinen festen Grenzwert gibt und man Aussagen über aktuale Unendlichkeiten äußern will.
Durch diesen variablen Grenzwert wird es unmöglich eine klare Aussage zu treffen. Die Aussage wird gewissermaßen unscharf!
Ich glaube inzwischen auch, dass die gesuchte Wahrscheinlichkeit nicht 1/9 ist, sondern unbestimmt zwischen 1/9 und 5/9 liegt.
Grüße
seeker
Edit:
Falls du recht hast, ist es keine reine Zufallszahl mehr - aber immer noch eine Zufallszahl.
Zufälligkeit bedeutet nicht, dass alle Wahrscheinlichkeiten gleich groß sein müssen: Sie bedeutet, dass es keine Wahrscheinlichkeit = 1 für eine bestimmte Wahl gibt.
Ja, aber die Frage ist auch in Zehnersystem gestellt. Ich glaube nicht, dass uns das weiterhilft.Skeltek hat geschrieben:Ich wollte nur deutlich machen, daß es keine Zufallszahl mehr ist, wenn man die Obergrenze für die Menge aus der man zieht genau auf z.B. 99999 festlegt. 99999 ist ein Wert, der nur so ist, weil wir im Zehnersystem rechnen.
Die Ziffern haben mit den Zahlen erst einmal wenig zu tun.
Ich könnte auch im Dreiersystem rechnen und dann fragen, ob bestimmte, definierbare Ziffernfolgen öfter als andere vorkommen. Das ist dann der Fall, wenn ich zum richtigen Zeitpunkt aufhöre zu Zählen.
Ich sage es noch einmal:
Das Grundproblem scheint mir zu sein, dass die Methode "Grenzwertbetrachtung" streng genommen ungenügend ist, wenn es keinen festen Grenzwert gibt und man Aussagen über aktuale Unendlichkeiten äußern will.
Durch diesen variablen Grenzwert wird es unmöglich eine klare Aussage zu treffen. Die Aussage wird gewissermaßen unscharf!
Ich glaube inzwischen auch, dass die gesuchte Wahrscheinlichkeit nicht 1/9 ist, sondern unbestimmt zwischen 1/9 und 5/9 liegt.
Grüße
seeker
Edit:
Skeltek, da muss ich widersprechen:Skeltek hat geschrieben:Ich wollte nur deutlich machen, daß es keine Zufallszahl mehr ist, wenn man die Obergrenze für die Menge aus der man zieht genau auf z.B. 99999 festlegt.
Falls du recht hast, ist es keine reine Zufallszahl mehr - aber immer noch eine Zufallszahl.
Zufälligkeit bedeutet nicht, dass alle Wahrscheinlichkeiten gleich groß sein müssen: Sie bedeutet, dass es keine Wahrscheinlichkeit = 1 für eine bestimmte Wahl gibt.
Grüße
seeker
Wissenschaft ... ist die Methode, kühne Hypothesen aufstellen und sie der schärfsten Kritik auszusetzen, um herauszufinden, wo wir uns geirrt haben.
Karl Popper
seeker
Wissenschaft ... ist die Methode, kühne Hypothesen aufstellen und sie der schärfsten Kritik auszusetzen, um herauszufinden, wo wir uns geirrt haben.
Karl Popper
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
Lasst mich das mal zusammenfassen.
Die relative Häufigkeit der Ziffer '1' schwankt zwischen 1/9 und 5/9 (+ epsilon), wenn man die Obergrenze N des betrachteten Zahlenbereiches [1,N] vergrößert. Für N gegen Unendlich nähert sich das Maximum (das jeweils bei Zahlen der Form '1999...9' angenommen wird) asymptotisch von oben der 5/9. Das Minimum (das jeweils für Zahlen der Form '999...9' angenommen wird) ist jeweils exakt 1/9.
Man kann diese relative Häufigkeit formal wie folgt schreiben
))
Dabei steht D[down]1[/down](N) für die erste Ziffer der Zahl N (im Zehnersystem) und S[down]1[/down](d) nimmt die Werte 1 bzw. 0 an, je nach dem ob d eine 1 oder eine andere Ziffer ist.
Man kann die Häufigkeiten H[down]N[/down] auf unterschiedliche Weise untersuchen und gelangt immer zu dem selben Ergebnis, nämlich dass H[down]N[/down] für N gegen Unendlich nicht konvergiert. Damit ist m.E. die Frage, wie häufig die '1' als erste Ziffer im Bereich der natürlichen Zahlen vorkommt, zunächst mal nicht definiert (jedenfalls nicht über den von uns betrachteten Ansatz).
Ein mögliches Problem ist, dass es kein Wahrscheinlichkeitsmaß bzw. keine Gleichverteilung auf der Menge der natürlichen Zahln {1, 2, ...} gibt, denn dazu müsste gelten

mit
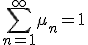
Aber die letzte Gleichung kann für ein konstantes, n-unabhängiges Maß nicht erfüllt sein. Unser 1/N funktioniert also irgendwie nicht,wie gewünscht.
Evtl. fällt mir aber dazu noch was ein.
Die relative Häufigkeit der Ziffer '1' schwankt zwischen 1/9 und 5/9 (+ epsilon), wenn man die Obergrenze N des betrachteten Zahlenbereiches [1,N] vergrößert. Für N gegen Unendlich nähert sich das Maximum (das jeweils bei Zahlen der Form '1999...9' angenommen wird) asymptotisch von oben der 5/9. Das Minimum (das jeweils für Zahlen der Form '999...9' angenommen wird) ist jeweils exakt 1/9.
Man kann diese relative Häufigkeit formal wie folgt schreiben
Dabei steht D[down]1[/down](N) für die erste Ziffer der Zahl N (im Zehnersystem) und S[down]1[/down](d) nimmt die Werte 1 bzw. 0 an, je nach dem ob d eine 1 oder eine andere Ziffer ist.
Man kann die Häufigkeiten H[down]N[/down] auf unterschiedliche Weise untersuchen und gelangt immer zu dem selben Ergebnis, nämlich dass H[down]N[/down] für N gegen Unendlich nicht konvergiert. Damit ist m.E. die Frage, wie häufig die '1' als erste Ziffer im Bereich der natürlichen Zahlen vorkommt, zunächst mal nicht definiert (jedenfalls nicht über den von uns betrachteten Ansatz).
Ein mögliches Problem ist, dass es kein Wahrscheinlichkeitsmaß bzw. keine Gleichverteilung auf der Menge der natürlichen Zahln {1, 2, ...} gibt, denn dazu müsste gelten
mit
Aber die letzte Gleichung kann für ein konstantes, n-unabhängiges Maß nicht erfüllt sein. Unser 1/N funktioniert also irgendwie nicht,wie gewünscht.
Evtl. fällt mir aber dazu noch was ein.
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
Vielleicht hilft uns das hier aus unserem Dilemma?
http://de.wikipedia.org/wiki/Maximum-Entropie-Methode
Die Maximum-Entropie-Methode besgat, dass in Abwesenheit von Information die Entropie der a-priori-Wahrscheinlichkeit zu maximieren, da jede andere Zuweisung willkürliche Einschränkungen der betrachteten Situation träfe. Die Maximum-Entropie-Methode legt sich so wenig wie möglich fest.
Die maximale Entropie scheint hier genau dann erreicht zu sein, wenn jede Anfangsziffer genau gleich häufig vorkommt.
Das löst das Problem nicht, macht es aber handhabbar...
Grüße
seeker
http://de.wikipedia.org/wiki/Maximum-Entropie-Methode
Die Maximum-Entropie-Methode besgat, dass in Abwesenheit von Information die Entropie der a-priori-Wahrscheinlichkeit zu maximieren, da jede andere Zuweisung willkürliche Einschränkungen der betrachteten Situation träfe. Die Maximum-Entropie-Methode legt sich so wenig wie möglich fest.
Die maximale Entropie scheint hier genau dann erreicht zu sein, wenn jede Anfangsziffer genau gleich häufig vorkommt.
http://de.wikipedia.org/wiki/Entropie_% ... theorie%29Beispiel Münzwurf
Maximale Entropie bei p=0.5
Bei einem Münzwurf sind idealerweise Kopf oder Zahl gleich wahrscheinlich. Wenn man die Entropie als Maß für die Ungewissheit auffasst, wird sie hier einen maximalen Wert aufweisen
Das löst das Problem nicht, macht es aber handhabbar...
Grüße
seeker
Grüße
seeker
Wissenschaft ... ist die Methode, kühne Hypothesen aufstellen und sie der schärfsten Kritik auszusetzen, um herauszufinden, wo wir uns geirrt haben.
Karl Popper
seeker
Wissenschaft ... ist die Methode, kühne Hypothesen aufstellen und sie der schärfsten Kritik auszusetzen, um herauszufinden, wo wir uns geirrt haben.
Karl Popper
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
Ich habe noch ein paar Experimente gemacht.
Und zwar bin ich davon weggegangen, die untere Grenze des zu betrachtenden Intervalls auf 1 festzulegen; statt des Intervall [1,N] betrachte ich [a,b] der Länge L=b-a. Nun berechne ich die Anzahl der Zahlen, die eine '1' als erste Ziffer haben in diesem Intervall. Nennen wir diese Funktion C(a,b); offensichtlich ist das zu berechnen mittels
C(a,b) = C(1,b) - C(1,a)
d.h. ich berechne die Zahl derartiger Zahlen im Intervall [1,b] und subtrahiere davon die unterhalb dieses Intervalls, also aus [1,a].
Zuletzt berechnen ich den Durchschnitt dieser Werte für C(a,b) bzw. ihrer Dichte; dabei gehe ich wie folgt vor: ich würfle das Intervall [a,b]; ich berechnen die Anzahl C(a,b) und dividiere durch die Länge L=b-a; d.h. C(a,b)/(b-a); zuletzt mittle ich über sehr viele dieser Werte.
Das Ergebnis liegt sehr nahe bei 1/9!
D.h. man kann schon eine Methode finden, derzufolge die erste Ziffer mit der Wahrscheinlichkeit 1/9 auftritt, allerdings muss man dazu zulassen, dass sich die Intervalle bzgl. Position und Größe zufällig auf der Zahlengerade verteilen (ich glaube, das hat hier auch schon mal jemand vorgeschlagen).
----------------
Edit:
Offensichtlich hängt das auch noch von der Verteilung der Intervalle ab - oder mein Zufallszahlengenerator spielt mir einen Streich. Ich habe jetzt jedenfalls eine neue Methode ausprobiert: ich betrachte die Wahrscheinlichkeit in Abhängigkeit von der Intervalllänge L und würfle nur den Anfangspunkt des Intervalls, also [a, a+L]. Die Wahrscheinlichkeit ist für kleine L relativ nahe bei 1/3 (passt das in etwa zu Benfords Gesetz?) um für größere L dann deutlich abzufallen; evtl. macht sich dann bemerkbar, dass ein Intervall der Länge L sich nicht mehr über viele Bereiche {100.., ..., 199, ..., 999...} erstreckt. Jedenfalls ist es schwierig, eine genügend gute und zufällige Überdeckung der Zahkengerade zu bekommen.
Anmerkung:
Die Funktion, die das Zählen übernimmt, habe ich wie folgt implementiert; sie nutzt die Tatsache (das hat hier schon mal jemand beobachtet), dass die Funktion gewissermaßen selbstähnlich ist für jeden (logarithmischen) Abschnitt [10[up]a[/up], 10[up]a+1[/up]]. Ich berechne zunächst für jede Zahl die nächst kleinere Zehnerpotenz (also für 113 z.B. die 100) und berechnen dann die Zahlen unterhalb von 100, also aus {1, 2, 3, ..., 10, 11, ..., 20, 21, ..., 999} die Zahlen {1, 10, 11, .., 19}, das sind genau 11 Stück, also 99/9 = (100-1)/9; allgemein (10[up]a[/up]-1)/9. Die Anzahl dieser Zahlen nenne ich p. Dann berechne ich die verbleibenden Zahlen, im Beispiel also {100, 101, ..., 113}. Die Anzahl nenne ich q. Das Ergebnis lautet demnach p+q.
Und zwar bin ich davon weggegangen, die untere Grenze des zu betrachtenden Intervalls auf 1 festzulegen; statt des Intervall [1,N] betrachte ich [a,b] der Länge L=b-a. Nun berechne ich die Anzahl der Zahlen, die eine '1' als erste Ziffer haben in diesem Intervall. Nennen wir diese Funktion C(a,b); offensichtlich ist das zu berechnen mittels
C(a,b) = C(1,b) - C(1,a)
d.h. ich berechne die Zahl derartiger Zahlen im Intervall [1,b] und subtrahiere davon die unterhalb dieses Intervalls, also aus [1,a].
Zuletzt berechnen ich den Durchschnitt dieser Werte für C(a,b) bzw. ihrer Dichte; dabei gehe ich wie folgt vor: ich würfle das Intervall [a,b]; ich berechnen die Anzahl C(a,b) und dividiere durch die Länge L=b-a; d.h. C(a,b)/(b-a); zuletzt mittle ich über sehr viele dieser Werte.
Das Ergebnis liegt sehr nahe bei 1/9!
D.h. man kann schon eine Methode finden, derzufolge die erste Ziffer mit der Wahrscheinlichkeit 1/9 auftritt, allerdings muss man dazu zulassen, dass sich die Intervalle bzgl. Position und Größe zufällig auf der Zahlengerade verteilen (ich glaube, das hat hier auch schon mal jemand vorgeschlagen).
----------------
Edit:
Offensichtlich hängt das auch noch von der Verteilung der Intervalle ab - oder mein Zufallszahlengenerator spielt mir einen Streich. Ich habe jetzt jedenfalls eine neue Methode ausprobiert: ich betrachte die Wahrscheinlichkeit in Abhängigkeit von der Intervalllänge L und würfle nur den Anfangspunkt des Intervalls, also [a, a+L]. Die Wahrscheinlichkeit ist für kleine L relativ nahe bei 1/3 (passt das in etwa zu Benfords Gesetz?) um für größere L dann deutlich abzufallen; evtl. macht sich dann bemerkbar, dass ein Intervall der Länge L sich nicht mehr über viele Bereiche {100.., ..., 199, ..., 999...} erstreckt. Jedenfalls ist es schwierig, eine genügend gute und zufällige Überdeckung der Zahkengerade zu bekommen.
Anmerkung:
Die Funktion, die das Zählen übernimmt, habe ich wie folgt implementiert; sie nutzt die Tatsache (das hat hier schon mal jemand beobachtet), dass die Funktion gewissermaßen selbstähnlich ist für jeden (logarithmischen) Abschnitt [10[up]a[/up], 10[up]a+1[/up]]. Ich berechne zunächst für jede Zahl die nächst kleinere Zehnerpotenz (also für 113 z.B. die 100) und berechnen dann die Zahlen unterhalb von 100, also aus {1, 2, 3, ..., 10, 11, ..., 20, 21, ..., 999} die Zahlen {1, 10, 11, .., 19}, das sind genau 11 Stück, also 99/9 = (100-1)/9; allgemein (10[up]a[/up]-1)/9. Die Anzahl dieser Zahlen nenne ich p. Dann berechne ich die verbleibenden Zahlen, im Beispiel also {100, 101, ..., 113}. Die Anzahl nenne ich q. Das Ergebnis lautet demnach p+q.
Code: Alles auswählen
unsigned long C( unsigned long N )
{
if ( N == 0 )
return 0;
if ( N < 10 )
return 1;
unsigned long a = (unsigned long) floor( log10( (double)N ) ) - 1;
unsigned long Na = (unsigned long) pow( (double)10.0, (double)a );
unsigned long Nb = 10 * Na;
unsigned long n = N - Nb;
unsigned long p = ( Nb - 1 ) / 9;
unsigned long q = ( n < Nb ) ? n + 1 : Nb;
return ( p + q );
}
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
Ich habe noch eine schöne Projektarbeit zum Thema "Das Gesetz der ersten Ziffer" gefunden:
http://www.google.de/url?sa=t&source=we ... OoDUnhAW7w
Der Link führt direkt zu einem Word-Dokument der Uni Kassel - nicht erschrecken!
Einiges, was wir schon herausgefunden haben, ist dort bestätigt.
Grüße
seeker
http://www.google.de/url?sa=t&source=we ... OoDUnhAW7w
Der Link führt direkt zu einem Word-Dokument der Uni Kassel - nicht erschrecken!
Einiges, was wir schon herausgefunden haben, ist dort bestätigt.
Grüße
seeker
Grüße
seeker
Wissenschaft ... ist die Methode, kühne Hypothesen aufstellen und sie der schärfsten Kritik auszusetzen, um herauszufinden, wo wir uns geirrt haben.
Karl Popper
seeker
Wissenschaft ... ist die Methode, kühne Hypothesen aufstellen und sie der schärfsten Kritik auszusetzen, um herauszufinden, wo wir uns geirrt haben.
Karl Popper
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
Darin wird insbs. das Benfordsche Gesetz behandelt; ich sehe aber nicht, wie diese Resultate zusammenpassen bzw. wieso im Falle der natürlichen Zahlen das Benfordsche Gesetz überhaupt eine Role spielen sollte; insbs. haben wir keine Skaleninvarianz, kein Wachstum, eigtl. auch keien zufälligen Zahen,s ondern eben gerade die natürlichen Zahlen
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
Das ist richtig.
Ich dachte eben, dass es den einen oder anderen Leser interessieren könnte.
Folgende Aussage fand ich dort noch interessant:
Ich stehe immer noch auf dem Standpunkt, dass die Häufigkeit der Anfangsziffern bei der Menge der natürlichen Zahlen (innerhalb von bestimmbaren Grenzen) unbestimmt ist. Ich glaube: Man kommt dem Problem nicht wirklich bei, wenn man endliche Teilmengen aus N betrachtet. Deshalb muss man diese Unbestimmtheit eben akzeptieren oder bei Bedarf zusätzliche Definitionen einführen.
Siehst du das anders?
Grüße
seeker
Ich dachte eben, dass es den einen oder anderen Leser interessieren könnte.
Folgende Aussage fand ich dort noch interessant:
Was bedeutet das? Bedeutet es, dass das Gesetz von Benford bei manchen unendlichen Folgen gilt oder bedeutet es wieder nur, dass es bei Teilmengen aus diesen Folgen gilt?Die unendlichen geometrischen Folgen erfüllen in den meisten Fällen das Gesetz von Benford, nämlich bei irrationalen Potenzen von 10 als Faktor – es gibt bekanntlich nur abzählbar viele rationale Zahlen im Gegensatz zu den überabzählbar vielen Irrationalen; bei z. B. hinreichen kleinen rationalen Werten a/bwird das Gesetz ebenfalls in guter Nährung erfüllt.
Wenn also eine Zahl zufällig aus einer unendlichen geometrischen Folge gewählt wird ist das Zustandekommen der ungleichen Verteilung der ersten Ziffer durch obigen Gedanken erklärt.
Ich stehe immer noch auf dem Standpunkt, dass die Häufigkeit der Anfangsziffern bei der Menge der natürlichen Zahlen (innerhalb von bestimmbaren Grenzen) unbestimmt ist. Ich glaube: Man kommt dem Problem nicht wirklich bei, wenn man endliche Teilmengen aus N betrachtet. Deshalb muss man diese Unbestimmtheit eben akzeptieren oder bei Bedarf zusätzliche Definitionen einführen.
Siehst du das anders?
Grüße
seeker
Grüße
seeker
Wissenschaft ... ist die Methode, kühne Hypothesen aufstellen und sie der schärfsten Kritik auszusetzen, um herauszufinden, wo wir uns geirrt haben.
Karl Popper
seeker
Wissenschaft ... ist die Methode, kühne Hypothesen aufstellen und sie der schärfsten Kritik auszusetzen, um herauszufinden, wo wir uns geirrt haben.
Karl Popper
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
Nach dem was ich jetzt weiß, ist dein Standpunkt gut nachvollziehbar; ich weigere mich aber immer noch, ihn letztlich zu akzeptieren.
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
OK, ich verstehe. Das kann ich wiederum gut nachvollziehen. 
Grüße
seeker
Wissenschaft ... ist die Methode, kühne Hypothesen aufstellen und sie der schärfsten Kritik auszusetzen, um herauszufinden, wo wir uns geirrt haben.
Karl Popper
seeker
Wissenschaft ... ist die Methode, kühne Hypothesen aufstellen und sie der schärfsten Kritik auszusetzen, um herauszufinden, wo wir uns geirrt haben.
Karl Popper
-
Skeltek
- Site Admin

- Beiträge: 5085
- Registriert: 25. Mär 2008, 23:51
- Wohnort: Stuttgart, Germany
- Kontaktdaten:
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
Die Kernbedingung auf Wikipedia:
p0:=0; //zum Zählen der Ziffern in den Mantissen
p1:=0;
p2:=0;
p3:=0;
p4:=0;
p5:=0;
p6:=0;
p7:=0;
p8:=0;
p9:=0;
n:=1;
while n<08150815 do
{s:=log(n) - floor(log(n)); //Die Mantisse des log raus ziehen uns als s speichern
for floor(s*10)==0 do p0:=P0+1; //hier speichern wir, wie oft die erste Ziffer(!also unvollständige Betrachtung) der Mantissen jeweils vorkommt
for floor(s*10)==1 do p0:=P1+1; // == ist doch zum vergleichen oder wie war das?
for floor(s*10)==2 do p0:=P2+1;
for floor(s*10)==3 do p0:=P3+1;
for floor(s*10)==4 do p0:=P4+1;
for floor(s*10)==5 do p0:=P5+1;
for floor(s*10)==6 do p0:=P6+1;
for floor(s*10)==7 do p0:=P7+1;
for floor(s*10)==8 do p0:=P8+1;
for floor(s*10)==9 do p0:=P9+1;
n:=+1};
print(p0 ... p9) // Ergebnisse ausdruckn halt
hab k.A. obs was bringt. Nen Beweis ist das net, aber vielleicht können wir ja mal guckn.
Also muss man nur prüfen, daß ob die Mantissen der zahlen eine homogene Verteilung aufweisen?Ein Datensatz ist eine Benford-Variable (das heißt, das benfordsche Gesetz gilt für diesen Datensatz), wenn die Mantissen der Logarithmen des Datensatzes in den Grenzen von 0 bis 1 gleichverteilt sind.
p0:=0; //zum Zählen der Ziffern in den Mantissen
p1:=0;
p2:=0;
p3:=0;
p4:=0;
p5:=0;
p6:=0;
p7:=0;
p8:=0;
p9:=0;
n:=1;
while n<08150815 do
{s:=log(n) - floor(log(n)); //Die Mantisse des log raus ziehen uns als s speichern
for floor(s*10)==0 do p0:=P0+1; //hier speichern wir, wie oft die erste Ziffer(!also unvollständige Betrachtung) der Mantissen jeweils vorkommt
for floor(s*10)==1 do p0:=P1+1; // == ist doch zum vergleichen oder wie war das?
for floor(s*10)==2 do p0:=P2+1;
for floor(s*10)==3 do p0:=P3+1;
for floor(s*10)==4 do p0:=P4+1;
for floor(s*10)==5 do p0:=P5+1;
for floor(s*10)==6 do p0:=P6+1;
for floor(s*10)==7 do p0:=P7+1;
for floor(s*10)==8 do p0:=P8+1;
for floor(s*10)==9 do p0:=P9+1;
n:=+1};
print(p0 ... p9) // Ergebnisse ausdruckn halt
hab k.A. obs was bringt. Nen Beweis ist das net, aber vielleicht können wir ja mal guckn.
Gödel für Dummies:
- Unentscheidbarkeit - Dieser Satz ist wahr.
- Unvollständig - Aussage A: Es existiert nur ein Element A.
- Widersprüchlich - Dieser Satz ist falsch.
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
Probiert's, ich habe wenig Hoffnung...
Ich möchte noch einmal darauf hinweisen, was wir aus meiner Sicht eigentlich tun:
Wir betrachten nicht die Häufigkeiten der Zahlen selbst, sondern nur die Häufigkeiten in den "Hausnummern" (=Ziffern), die wir den Zahlen verpasst haben.
Durch das Zählen z.B. im Zehnersystem legen wir ein Muster über die Zahlen. Das Überraschende ist nun, dass ein scheinbar homogenes Muster, wie das Zehnersystem, doch nicht so homogen ist, wie gedacht.
Der (scheinbare) Widerspruch liegt nun darin, dass es offensichtlich nicht sein kann, dass dieses doch willkürliche Muster irgendeinen Einfluss auf die Zahlen selbst haben kann: Jede Zahl kommt genau 1x vor. Daher haben wir selbstverständlich eine Gleichverteilung aller Zahlen in N.
Beispiel einer anderen Frage:
Wie hoch ist der prozentuale Anteil der natürlichen Zahlen, die mindestens einmal die Ziffer 9 enthalten?
Antwort: 100%.
Der Anteil der höchstens n-stelligen Zahlen mit Neunen beträgt (1 - 0,9^n) * 100%. Weil 0,9^n gegen 0 geht, konvergiert der gefragte Prozentsatz gegen 100%.
Dies gilt auch für jede andere Ziffer. Auch ohne Grenzwertbetrachtung ist es leicht einzusehen, dass bei Zahlen mit beliebig vielen Ziffern alle Ziffern vertreten sein werden.
Wie ist es nun, wenn man fragt:
Wie hoch ist der prozentuale Anteil der natürlichen Zahlen, die mindestens zweimal die Ziffer 9 enthalten?
Es kommt wieder 100% heraus.
Auch bei 3x, 4x, 5x,...
Ist es im Umkehrschluss also unmöglich eine Zufallszahl aus N zu ziehen, die nicht beliebig viele Ziffern (0-9) enthält?
Mich interessiert die Frage, ob man aus N überhaupt eine Zufallszahl ziehen kann immer noch sehr.
Im Moment glaube ich, dass das zwar prinzipiell möglich ist, dass es aber keine Zahl ist, die man aufschreiben kann.
Es ist nicht einmal eine Zahl, die man prinzipiell aufschreiben kann!
Ich meine, dass man nicht umhin kommt so eine Zahl als unbestimmt zu bezeichnen.
Es fragt sich dabei: Was ist eine Zahl? Ist eine Zahl, die keinen bestimmten Wert hat überhaupt noch eine Zahl?
Grüße
seeker
Ich möchte noch einmal darauf hinweisen, was wir aus meiner Sicht eigentlich tun:
Wir betrachten nicht die Häufigkeiten der Zahlen selbst, sondern nur die Häufigkeiten in den "Hausnummern" (=Ziffern), die wir den Zahlen verpasst haben.
Durch das Zählen z.B. im Zehnersystem legen wir ein Muster über die Zahlen. Das Überraschende ist nun, dass ein scheinbar homogenes Muster, wie das Zehnersystem, doch nicht so homogen ist, wie gedacht.
Der (scheinbare) Widerspruch liegt nun darin, dass es offensichtlich nicht sein kann, dass dieses doch willkürliche Muster irgendeinen Einfluss auf die Zahlen selbst haben kann: Jede Zahl kommt genau 1x vor. Daher haben wir selbstverständlich eine Gleichverteilung aller Zahlen in N.
Beispiel einer anderen Frage:
Wie hoch ist der prozentuale Anteil der natürlichen Zahlen, die mindestens einmal die Ziffer 9 enthalten?
Antwort: 100%.
Der Anteil der höchstens n-stelligen Zahlen mit Neunen beträgt (1 - 0,9^n) * 100%. Weil 0,9^n gegen 0 geht, konvergiert der gefragte Prozentsatz gegen 100%.
Dies gilt auch für jede andere Ziffer. Auch ohne Grenzwertbetrachtung ist es leicht einzusehen, dass bei Zahlen mit beliebig vielen Ziffern alle Ziffern vertreten sein werden.
Wie ist es nun, wenn man fragt:
Wie hoch ist der prozentuale Anteil der natürlichen Zahlen, die mindestens zweimal die Ziffer 9 enthalten?
Es kommt wieder 100% heraus.
Auch bei 3x, 4x, 5x,...
Ist es im Umkehrschluss also unmöglich eine Zufallszahl aus N zu ziehen, die nicht beliebig viele Ziffern (0-9) enthält?
Mich interessiert die Frage, ob man aus N überhaupt eine Zufallszahl ziehen kann immer noch sehr.
Im Moment glaube ich, dass das zwar prinzipiell möglich ist, dass es aber keine Zahl ist, die man aufschreiben kann.
Es ist nicht einmal eine Zahl, die man prinzipiell aufschreiben kann!
Ich meine, dass man nicht umhin kommt so eine Zahl als unbestimmt zu bezeichnen.
Es fragt sich dabei: Was ist eine Zahl? Ist eine Zahl, die keinen bestimmten Wert hat überhaupt noch eine Zahl?
Grüße
seeker
Grüße
seeker
Wissenschaft ... ist die Methode, kühne Hypothesen aufstellen und sie der schärfsten Kritik auszusetzen, um herauszufinden, wo wir uns geirrt haben.
Karl Popper
seeker
Wissenschaft ... ist die Methode, kühne Hypothesen aufstellen und sie der schärfsten Kritik auszusetzen, um herauszufinden, wo wir uns geirrt haben.
Karl Popper
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
@skeltek: Interessante Idee; das kann man dann aber auch exakt berechnen.
Laut Benford ist die Darstellung einer Zahl bzgl. einer bestimmten Basis b sowie des Logarithmus zu einer bestimmten Basis b irrelevant. Nehmen wir der Einfachheit halber also b=10.
Dann können wir jede natürliche Zahl n darstellen als
n = x 10[up]k[/up]
Dabei ist 1 < x < 10
der Zehnerlogarithmus lautet
log[down]10[/down]n = log[down]10[/down]x + k
Die Mantisse davon erhält man durch Subtrahieren des ganzzahligen Anteils; diesen ganzzahligen Anteil einer beliebigen Zahl z schreibe ich als [z]. D.h. man betrachtet die Mantissenfunktion bzgl. des Zehnerlogarithmus von n:
M(n) = log[down]10[/down]n - [log[down]10[/down]n] = log[down]10[/down]n - [log[down]10[/down]n] = log[down]10[/down]x
Der zweite Term fällt weg, da x[down]0[/down] < 10 vorausgesetzt war; damit ist aber [log[down]10[/down]x] = 0.
Offensichtlich ist k für diese Betrachtung irrelevant (da immer ganzzahlig), d.h. es genügt, den Zahlenbereich [1,10[ mit k=0 zu betrachten. Alle anderen Zahlenbereiche [10,100[, usw. verhalten sich dann analog.
Der nächste Schritt wäre nun, aus der Mantissenfunktion M(n) eine Verteilungsfunktion zu berechnen.
Laut Benford ist die Darstellung einer Zahl bzgl. einer bestimmten Basis b sowie des Logarithmus zu einer bestimmten Basis b irrelevant. Nehmen wir der Einfachheit halber also b=10.
Dann können wir jede natürliche Zahl n darstellen als
n = x 10[up]k[/up]
Dabei ist 1 < x < 10
der Zehnerlogarithmus lautet
log[down]10[/down]n = log[down]10[/down]x + k
Die Mantisse davon erhält man durch Subtrahieren des ganzzahligen Anteils; diesen ganzzahligen Anteil einer beliebigen Zahl z schreibe ich als [z]. D.h. man betrachtet die Mantissenfunktion bzgl. des Zehnerlogarithmus von n:
M(n) = log[down]10[/down]n - [log[down]10[/down]n] = log[down]10[/down]n - [log[down]10[/down]n] = log[down]10[/down]x
Der zweite Term fällt weg, da x[down]0[/down] < 10 vorausgesetzt war; damit ist aber [log[down]10[/down]x] = 0.
Offensichtlich ist k für diese Betrachtung irrelevant (da immer ganzzahlig), d.h. es genügt, den Zahlenbereich [1,10[ mit k=0 zu betrachten. Alle anderen Zahlenbereiche [10,100[, usw. verhalten sich dann analog.
Der nächste Schritt wäre nun, aus der Mantissenfunktion M(n) eine Verteilungsfunktion zu berechnen.
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
Die Frage scheint doch eher zu sein, ob das Universum überhaupt teilbar ist. Aus meinem einfachen Verständnis für die Natur glaube ich eher nicht.seeker hat geschrieben:Es fragt sich dabei: Was ist eine Zahl? Ist eine Zahl, die keinen bestimmten Wert hat überhaupt noch eine Zahl?
Was ist aber, wenn ich etwas unteilbares teile?
Was ist dann dazwischen?
Gruß
Peter
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
Tja, ich habe das mal gemacht; mein kleines Programm sieht wie folgt aus:
Die Funktion M(n) berechnet die Mantisse des Logarithmus (zur Basis 10) der übergebenen Zahl.
Ich verteile die Mantissen auf ein Histogramm hist[]. Dieses zeigt bereits ab einigen 1000 Zahlen einen perfekt exponentiellen Verlauf, d.h.die Werte im Histogramm werden extrem gut durch eine Gleichung der Form
h(x) = const 10[up]x[/up]
angenähert. Es liegt also - nach erster Durchsicht - keine Gleichverteilung vor.
Code: Alles auswählen
// log_distr.cpp : Definiert den Einstiegspunkt für die Konsolenanwendung.
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
const long max_idx = 5000;
const long long max_n = 100000000;
long long hist[max_idx];
long double M( long long n )
{
long double L = log10( (long double)n );
return L - floor( L );
}
int main( int argc, char * argv[] )
{
for ( long idx=0; idx<max_idx; idx++ )
hist[idx] = 0;
for ( long long n=1; n<max_n; n++ )
{
long idx = (long)((long double)max_idx * M(n) );
++hist[idx];
}
for ( long idx=0; idx<max_idx; idx++ )
printf( "%ld; %ld\n", idx, hist[idx] );
return 0;
}
Ich verteile die Mantissen auf ein Histogramm hist[]. Dieses zeigt bereits ab einigen 1000 Zahlen einen perfekt exponentiellen Verlauf, d.h.die Werte im Histogramm werden extrem gut durch eine Gleichung der Form
h(x) = const 10[up]x[/up]
angenähert. Es liegt also - nach erster Durchsicht - keine Gleichverteilung vor.
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
Natürlich ist eine Zahl, die keinen bestimmten Wert hat, noch eine Zahl. Die Mathematiker haben gelernt, mit so etwas umzugehen => Ich starte mal einen neuen Thread dazu
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
Ich möchte diese Aussage noch durch ein Beispiel ergänzen, um sie klarer zu machen:seeker hat geschrieben:Ich möchte noch einmal darauf hinweisen, was wir aus meiner Sicht eigentlich tun:
Wir betrachten nicht die Häufigkeiten der Zahlen selbst, sondern nur die Häufigkeiten in den "Hausnummern" (=Ziffern), die wir den Zahlen verpasst haben.
Durch das Zählen z.B. im Zehnersystem legen wir ein Muster über die Zahlen. Das Überraschende ist nun, dass ein scheinbar homogenes Muster, wie das Zehnersystem, doch nicht so homogen ist, wie gedacht.
Ihr kennt doch Lotto?
Nehmen wir also diese Lottoziehmaschine und füllen sie mit 200 Kugeln. Auf die Kugeln schreiben wir jeweils eine Zahl drauf, und zwar so, dass auf den Kugeln die Zahlen 0-199 stehen.
So!
Nun setzen wir die Maschine in Gang, lassen eine Kugel ziehen, geben sie zurück in die Maschine, lassen wieder ziehen, usw.
Unsere Überlegungen besagen nun, dass die Zahlen auf den gezogenen Kugeln häufiger mit einer 1 beginnen als mit einer 9. Das ist auch so - unbestritten!
Dies sagt aber überhaupt nichts darüber aus, wie die groß die Wahrscheinlichkeit irgendeiner Kugel ist gezogen zu werden.
Selbstverständlich ist die Wahrscheinlichkeit einer Kugel gezogen zu werden unabhängig davon, was auf der Kugel für eine Zahl steht.
Sie ist für alle Kugeln immer exakt gleich groß. Dies ist unabhängig davon, wie viele Kugeln in der Maschine sind.
Von dieser Basis ausgehend möchte ich weiterdenken:
Was passiert nun, wenn ich unendlich viele Kugeln in die Maschine einfülle?
Es stellen sich folgende Teilfragen:
1. Kann man unendlich viele Kugeln einfüllen?
2. Kann die Maschine unendlich viele Kugeln so durchmischen, dass sie in der Lage ist eine Kugel zufällig zu ziehen?
3. Welche Zahl kann auf einer so gezogenen Kugel draufstehen und welche nicht? Kann da eine Zahl draufstehen? Falls ja, welche Eigenschaften hat sie?
Gewöhnliche physikalische Grenzen sollen dabei zunächst unberücksichtigt bleiben. Es geht mir rein um die Logik.
So darf die Maschine meinetwegen durchaus unendlich groß sein und unendlich lange mischen bevor sie eine Kugel zieht.
Bei 1. tendiere ich zu einem JA, bei 2. tendiere ich zu einem vorsichtigen JA und bei 3. wird es wirklich schwierig...
Grüße
seeker
Grüße
seeker
Wissenschaft ... ist die Methode, kühne Hypothesen aufstellen und sie der schärfsten Kritik auszusetzen, um herauszufinden, wo wir uns geirrt haben.
Karl Popper
seeker
Wissenschaft ... ist die Methode, kühne Hypothesen aufstellen und sie der schärfsten Kritik auszusetzen, um herauszufinden, wo wir uns geirrt haben.
Karl Popper
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
1. Kann man unendlich viele Kugeln einfüllen?
2. Kann die Maschine unendlich viele Kugeln so durchmischen, dass sie in der Lage ist eine Kugel zufällig zu ziehen?
3. Welche Zahl kann auf einer so gezogenen Kugel draufstehen und welche nicht? Kann da eine Zahl draufstehen? Falls ja, welche Eigenschaften hat sie?
Bei 1. tendiere ich zu "ja"; Georg Cantor hat uns genau das gezeigt.
Bei 2. tendiere ich auch zu ja, wobei dazu keine "Konstruktion" möglich zu sein scheint.
Bei 3. behaupte ich, dass grundsätzlich jede Kugel gezogen werden kann; die Frage ist, wie zufällig das ist und ob eine Gleichverteilung existieren kann
Ich habe mit ein paar Mathematikern gesprochen und die haben mir gesagt, dass es a) eine "natural density interpretation" gibt, die aber das o.g. Problem nicht löst, da sie die Grenzwerte 1/9 und 5/9 (oder was auch immer) nicht zusammenbringt; und dass es b) keine konsistente Möglichkeit gibt, eine Gleichverteilung über einem unendlichen Bereich und damit über den natürlichen Zahlen zu konstruieren.
http://en.wikipedia.org/wiki/Natural_density
Klingt erst mal nach Kapitulation vor dem Unendlichen ... ich bin aber immer noch nicht bereit, da aufzugeben
2. Kann die Maschine unendlich viele Kugeln so durchmischen, dass sie in der Lage ist eine Kugel zufällig zu ziehen?
3. Welche Zahl kann auf einer so gezogenen Kugel draufstehen und welche nicht? Kann da eine Zahl draufstehen? Falls ja, welche Eigenschaften hat sie?
Bei 1. tendiere ich zu "ja"; Georg Cantor hat uns genau das gezeigt.
Bei 2. tendiere ich auch zu ja, wobei dazu keine "Konstruktion" möglich zu sein scheint.
Bei 3. behaupte ich, dass grundsätzlich jede Kugel gezogen werden kann; die Frage ist, wie zufällig das ist und ob eine Gleichverteilung existieren kann
Ich habe mit ein paar Mathematikern gesprochen und die haben mir gesagt, dass es a) eine "natural density interpretation" gibt, die aber das o.g. Problem nicht löst, da sie die Grenzwerte 1/9 und 5/9 (oder was auch immer) nicht zusammenbringt; und dass es b) keine konsistente Möglichkeit gibt, eine Gleichverteilung über einem unendlichen Bereich und damit über den natürlichen Zahlen zu konstruieren.
http://en.wikipedia.org/wiki/Natural_density
Klingt erst mal nach Kapitulation vor dem Unendlichen ... ich bin aber immer noch nicht bereit, da aufzugeben
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
In einer endlichen Welt gibt es auch nur endlich viele Kugeln. Die Unendlichkeit ist nur ein Symbol (die liegende Acht). Aber gesehen hat sie noch keiner.seeker hat geschrieben: Was passiert nun, wenn ich unendlich viele Kugeln in die Maschine einfülle?
Es stellen sich folgende Teilfragen:
1. Kann man unendlich viele Kugeln einfüllen?
Also meine Antwort ist Nein.
Geht doch auch schon mit endlich vielen Kuegeln. Je mehr Kugeln, umso "zufälliger" ist der Zufall. Bei hypothetisch unendlich vielen Kugeln wär der Zufall also auch "unendlich gut".seeker hat geschrieben:2. Kann die Maschine unendlich viele Kugeln so durchmischen, dass sie in der Lage ist eine Kugel zufällig zu ziehen?
Die Zahl, die da drauf stünde hätte mit 100%iger Wahrscheinlichkeit unendlich viele Stellen/Ziffern, denn bei unendlich vielen Zahlen gibt es auch unendlich viel mehr unendlich große Zahlen als es "normale" Zahlen gibt, wie 7 oder 19.seeker hat geschrieben:3. Welche Zahl kann auf einer so gezogenen Kugel draufstehen und welche nicht? Kann da eine Zahl draufstehen? Falls ja, welche Eigenschaften hat sie?
Und das ist der Grund, warum ich die Unendlichkeit nicht mag. Da wird nämlich immer ganz schnell alles "unendlich" kompliziert.
Sorry für die etwas unqualifizierte Antwort. Aber bei den Unendlichkeit bin ich immer der Meinung, die wurde nur von den Mathematikern erfunden - eine Kapitulation vor dem Großen oder Kleinen oder generell dem Unvorstellbaren. Hoffe, jetzt schlägt mich keiner.
Gruß
Mac
Das Gehirn ist nur so schlau wie sein Besitzer.
-
Skeltek
- Site Admin

- Beiträge: 5085
- Registriert: 25. Mär 2008, 23:51
- Wohnort: Stuttgart, Germany
- Kontaktdaten:
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
Ich dachte immer Mathematiker hätten die Unendlichkeit erfunden, aber die Physiker interpretieren sie falsch.Maclane hat geschrieben: Aber bei den Unendlichkeit bin ich immer der Meinung, die wurde nur von den Mathematikern erfunden - eine Kapitulation vor dem Großen oder Kleinen oder generell dem Unvorstellbaren.
Gödel für Dummies:
- Unentscheidbarkeit - Dieser Satz ist wahr.
- Unvollständig - Aussage A: Es existiert nur ein Element A.
- Widersprüchlich - Dieser Satz ist falsch.
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
Die Mathematiker haben das nicht erfunden, sondern nur formalisiert; Unendlich "existiert" gewissermaßen als Möglichkeit, man kann es nicht einfach ausschließen, ohne in Probleme zu laufen.
Schaut euch doch mal http://en.wikipedia.org/wiki/Natural_density an
Schaut euch doch mal http://en.wikipedia.org/wiki/Natural_density an
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
Es ist keine Kapitulation - im Gegenteil: Es ist ein Ringen darum über das Unendliche dennoch Aussagen machen zu können.Maclane hat geschrieben:Aber bei den Unendlichkeit bin ich immer der Meinung, die wurde nur von den Mathematikern erfunden - eine Kapitulation vor dem Großen oder Kleinen oder generell dem Unvorstellbaren.
Grüße
seeker
Grüße
seeker
Wissenschaft ... ist die Methode, kühne Hypothesen aufstellen und sie der schärfsten Kritik auszusetzen, um herauszufinden, wo wir uns geirrt haben.
Karl Popper
seeker
Wissenschaft ... ist die Methode, kühne Hypothesen aufstellen und sie der schärfsten Kritik auszusetzen, um herauszufinden, wo wir uns geirrt haben.
Karl Popper
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
Ich fasse das ganze nochmals kurz zusammen und schließe das Thema damit ab.
Wir gehen aus von der Menge der natürlichen Zahlen N, sowie der Teilmenge der ersten n Zahlen N(n) = {1, 2, ..., n}
Wir definieren eine Untermenge Z[down]1[/down], nämlich die Menge der Zahlen, die mit der Ziffer '1' beginnt, also Z[down]1[/down] = {1, 10, 11, ..., 19, 100, 101, ...}. Dann definieren wir eine weitere Untermenge Z[down]1[/down](n), nämlich die Menge der Zahlen, die mit der Ziffer '1' beginnt und die kleiner gleich n sind. Formal ist das Z[down]1[/down](n) = Z[down]1[/down] ∩ N(n)
Wir betrachten die Anzahl der Elemente dieser Menge |Z[down]1[/down](n)|.
Dann definieren wir die kleinste obere bzw. größte untere Schranke für die sogenannte Dichte
p(n) = |Z[down]1[/down](n)| / |N(n)|
für den Fall, dass wir n gegen Unendlich gehen lassen, d.h. formal den sogenannten Limes Superior und den Limes Inferior
p[up]+[/up] = lim sup p(n)
p[down]-[/down] = lim inf p(n)
Die sogenannte natürliche Dichte p erhält man für den Fall, dass die beiden Grenzwerte übereinstimmen, d.h.
p = p[up]+[/up] = p[down]-[/down]
Nur: in unserem Fall haben wir die beiden Grenzwerte ja bereits berechnet, nämlich
p[up]+[/up] = 5/9
p[down]-[/down] = 1/9
und festgestellt, dass sie nicht übereinstimmen. Damit lässt sich die natürliche Dichte p für die von uns diskutierte Menge Z[down]1[/down] nicht definieren. Die Schlussfolgerung - die mir persönlich nicht gefällt, die ich aber akzeptieren muss - ist, dass die Dichte bzw. relative Häufigkeit der Zahlen die mit einer '1' als erster Ziffer beginnen, nicht definiert werden kann! Generell besagt die Mathematik also, dass es die Eigenschaft "eine zufällig gewürfelte natürliche Zahl beginnt mit einer Wahrscheinlichkeit von p mit einer '1' als erster Ziffer" schlichtweg nicht gibt.
Ich denke, mit der Erkenntnis können wir diese "Nebenrechnung" abschließen, oder?
Wir gehen aus von der Menge der natürlichen Zahlen N, sowie der Teilmenge der ersten n Zahlen N(n) = {1, 2, ..., n}
Wir definieren eine Untermenge Z[down]1[/down], nämlich die Menge der Zahlen, die mit der Ziffer '1' beginnt, also Z[down]1[/down] = {1, 10, 11, ..., 19, 100, 101, ...}. Dann definieren wir eine weitere Untermenge Z[down]1[/down](n), nämlich die Menge der Zahlen, die mit der Ziffer '1' beginnt und die kleiner gleich n sind. Formal ist das Z[down]1[/down](n) = Z[down]1[/down] ∩ N(n)
Wir betrachten die Anzahl der Elemente dieser Menge |Z[down]1[/down](n)|.
Dann definieren wir die kleinste obere bzw. größte untere Schranke für die sogenannte Dichte
p(n) = |Z[down]1[/down](n)| / |N(n)|
für den Fall, dass wir n gegen Unendlich gehen lassen, d.h. formal den sogenannten Limes Superior und den Limes Inferior
p[up]+[/up] = lim sup p(n)
p[down]-[/down] = lim inf p(n)
Die sogenannte natürliche Dichte p erhält man für den Fall, dass die beiden Grenzwerte übereinstimmen, d.h.
p = p[up]+[/up] = p[down]-[/down]
Nur: in unserem Fall haben wir die beiden Grenzwerte ja bereits berechnet, nämlich
p[up]+[/up] = 5/9
p[down]-[/down] = 1/9
und festgestellt, dass sie nicht übereinstimmen. Damit lässt sich die natürliche Dichte p für die von uns diskutierte Menge Z[down]1[/down] nicht definieren. Die Schlussfolgerung - die mir persönlich nicht gefällt, die ich aber akzeptieren muss - ist, dass die Dichte bzw. relative Häufigkeit der Zahlen die mit einer '1' als erster Ziffer beginnen, nicht definiert werden kann! Generell besagt die Mathematik also, dass es die Eigenschaft "eine zufällig gewürfelte natürliche Zahl beginnt mit einer Wahrscheinlichkeit von p mit einer '1' als erster Ziffer" schlichtweg nicht gibt.
Ich denke, mit der Erkenntnis können wir diese "Nebenrechnung" abschließen, oder?
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
Skeltek
- Site Admin

- Beiträge: 5085
- Registriert: 25. Mär 2008, 23:51
- Wohnort: Stuttgart, Germany
- Kontaktdaten:
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
Mir kam grade in den Sinn, daß eine zufälliger Wert irgendwo auf der reelen Zahlengeraden sein müsste. Wenn man diesen Wert nur als 1 setzt, könnte man annehmen, daß links und rechts davon den nächsten Wert zu würfeln ca gleich hoch angenommen werden kann, bekommt man automatisch eine von einer Exponentialfunktion abhängige Zufallsrelation? Das heißt daß der nächste Wert zwischen 0 und 1 liegt ist genauso wahrscheinlich wie daß er rechts von der 1 liegt? Also wenn man nun den reelen positiven Zahlenraum betrachtet.
Gödel für Dummies:
- Unentscheidbarkeit - Dieser Satz ist wahr.
- Unvollständig - Aussage A: Es existiert nur ein Element A.
- Widersprüchlich - Dieser Satz ist falsch.
Re: Rolle des Zufalls in der Physik:"Nebenrechnungen"
verstehe ich nicht; über welchen Wert auf der Zahlengerade sprichst du? und was willst du festlegen?
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
