Seite 1 von 1
Welcher Planet ist der Erde am nähsten?
Verfasst: 23. Mär 2019, 20:07
von Frank
Gestatten, es ist der Merkur.

Ist natürlich alles eine Sache der Perspektive

 https://www.sueddeutsche.de/wissen/erdn ... -1.4369409
https://www.sueddeutsche.de/wissen/erdn ... -1.4369409
Re: Welcher Planet ist der Erde am nähsten?
Verfasst: 24. Mär 2019, 10:13
von tomS
Das ist sehr seltsam, und da würde mich die ursprüngliche Quelle interessieren.
Wenn man - in sehr guter Näherung - die Bahnen der Planeten als kreisförmig ansetzt, erhält man eine Bahnkurve
z(t) = r exp[iωt]
Zwischen Bahnradius und Frequenz besteht der Zusammenhang
GM = ω²r³ (drittes Keplersches Gesetz)
Der Abstand d₁₂(t) zweier Planeten lautet
d₁₂(t) =|z₁(t) - z₂(t)|
d₁₂²(t) = r₁² + r₂² - 2r₁r₂ cos(ω₁-ω₂)t
Zur Berechnung des
mittleren Abstandsquadrates D₁₂² integriert man über eine Periode, die durch die Differenz der Frequenzen ω₁-ω₂ definiert ist. Damit folgt
D₁₂² = r₁² + r₂²
D.h. das mittlere Abstandsquadrat ist gerade durch die Bahnradien definiert.
Nun weichen die Bahnen natürlich von idealen Kreisbahnen ab, d.h. weder die Radien noch die Geschwindigkeiten entlang der Bahnen sind konstant.
Aber diese Abweichungen sind klein!
Für den tatsächlichen Radius R sowie die Frequenz Ω entlang der Bahnkurve gilt.
R(φ) = r (1 - e cosφ)
Ω(φ) = ω (1 + 2e cosφ)
D.h. insgs. darf man Abweichungen von der o.g. Form von D₁₂² in der Größenordnung der Exzentrizität e erwarten. Nun ist diese mit 0.206 für den Merkur recht groß, dennoch wundert mich die Aussage sehr.
In Astronomischen Einheiten gilt für die großen Halbachsen von Merkur, Venus und Erde a = 0.387, 0.723, 1. Die unkorrigierten mittleren Abstandsquadrate D² der Erde zu Merkur bzw. Venus lauten 1.15 bzw. 1.52. Die Größenordnung des korrigierten Abstandsquadrates für Merkur liegt bei (1 + 0.206) * 1.15 = 1.39 < 1.52.
Wo liegt mein Denkfehler?
EDIT:
Hier ist der Artikel:
Venus is not Earth’s closest neighbor
Re: Welcher Planet ist der Erde am nähsten?
Verfasst: 24. Mär 2019, 11:16
von Herr5Senf
Hier gibt's die Rechnung von den "anderen"
https://physicstoday.scitation.org/do/1 ... 312a/full/
dort Formel 1: Ergebnis Venus 1,14AU und Merkur 1,04AU
Grüße Dip
Re: Welcher Planet ist der Erde am nähsten?
Verfasst: 24. Mär 2019, 11:53
von tomS
Danke, habe das auch gefunden und den Beitrag oben ergänzt. Ich kann deren Rechnung nicht nachvollziehen.
Re: Welcher Planet ist der Erde am nähsten?
Verfasst: 24. Mär 2019, 14:16
von Herr5Senf
Ist ja sowieso ein Fall für Ralf und nicht für uns

schon mal
Grüße Dip
Re: Welcher Planet ist der Erde am nähsten?
Verfasst: 24. Mär 2019, 14:34
von tomS
Ich denke, die Formel in dem Artikel ist falsch!
Wenn man die Radien gleichsetzt, müsste Null rauskommen - tut es aber nicht.
Und wenn ich die Rechnung durchführe, komme ich auf die Differenz der Radien, nicht auf deren Summe.
Re: Welcher Planet ist der Erde am nähsten?
Verfasst: 24. Mär 2019, 18:14
von ralfkannenberg
Herr5Senf hat geschrieben: ↑24. Mär 2019, 14:16
Ist ja sowieso ein Fall für Ralf und nicht für uns

schon mal
Nein, dieser Brain-Teaser ist nichts für mich, aber ich habe im astronews schon meine Meinung dazu geschrieben.
Man müsste eben erst einmal definieren, was man überhaupt berechnen will und über welche Zeiträume man da mitteln will etc. etc. und dann schauen, ob die im Artikel angegebene Definition diese Erwartung überhaupt erfüllt.
Freundliche Grüsse, Ralf
Re: Welcher Planet ist der Erde am nähsten?
Verfasst: 24. Mär 2019, 18:15
von tomS
dann auf astronews ...
Re: Welcher Planet ist der Erde am nähsten?
Verfasst: 24. Mär 2019, 18:20
von Frank
tomS hat geschrieben: ↑24. Mär 2019, 18:15
dann auf astronews ...
Warum sollte man das auch auf Abenteuer Universum besprechen.......

Re: Welcher Planet ist der Erde am nähsten?
Verfasst: 24. Mär 2019, 18:25
von Frank
ralfkannenberg hat geschrieben: ↑24. Mär 2019, 18:14
Man müsste eben erst einmal definieren, was man überhaupt berechnen will und über welche Zeiträume man da mitteln will etc. etc.
Doch nun rechnen Astronomen in der Zeitschrift Physics Today vor, dass man die Sache ganz anders sehen sollte. Die Frage nach dem erdnächsten Planeten hängt nämlich von der Definition der "Nähe" ab: Ist tatsächlich der Planet gemeint, welcher der Erde gelegentlich am nächsten kommt? Die Astronomen argumentieren: Eigentlich sollte es um den Planeten gehen, dessen mittlerer Abstand zur Erde am kürzesten ist. Also jener Planet, auf den wir Menschen an den meisten Tagen deuten müssten, wenn es darum geht, welcher Planet soeben am nächsten ist. So gesehen fällt die Antwort verblüffend aus: Der erdnächste Planet ist Merkur.
https://www.sueddeutsche.de/wissen/erdn ... -1.4369409
Ich habe die Definition verstanden , was man berechnen wollte(denn man hat es ja getan). .......
Re: Welcher Planet ist der Erde am nähsten?
Verfasst: 24. Mär 2019, 19:44
von tomS
Ich habe die Definition auch verstanden und die Rechnung nachvollzogen. Ich finde - bis auf ein Vorzeichen - den selben Term. Das Vorzeichen ist aber entscheidend! Auf Astronews habe ich um die Überprüfung meiner Rechnung gebeten.
Re: Welcher Planet ist der Erde am nähsten?
Verfasst: 24. Mär 2019, 21:12
von tomS
Nach weiterer Diskussion: das Ergebnis der Autoren ist korrekt.
Sehr spannend:
Plot für 9.6 AE = Saturn
Man erkennt, dass für den Saturn die Erde bei 1 AE der im Mittel näheste Planet ist, Venus, Merkur und Sonne sowie Mars und Jupiter sind im Mittel weiter entfernt.
Für den Pluto mit ca. 40 AE ist der Jupiter der im Mittel nächste Planet.
Re: Welcher Planet ist der Erde am nähsten?
Verfasst: 24. Mär 2019, 21:17
von Frank
Ich konnte mir auch nicht vorstellen, dass die Autoren eine Rechnung veröffentlichen, wennn sie nicht zig mal gegen gerechnet ist.
Also können wir festhalten, dass die Venus zwar der Erde am nähsten kommt, aber der Merkur die meiste Zeit der "Nachbarplanet " der Erde ist?
Re: Welcher Planet ist der Erde am nähsten?
Verfasst: 24. Mär 2019, 21:25
von tomS
Frank hat geschrieben: ↑24. Mär 2019, 21:17
... aber der Merkur die “meiste Zeit” der Nachbarplanet der Erde ist?
Ja, wenn du es so formulieren willst.
Re: Welcher Planet ist der Erde am nähsten?
Verfasst: 24. Mär 2019, 21:46
von ralfkannenberg
tomS hat geschrieben: ↑24. Mär 2019, 21:12
Man erkennt, dass für den Saturn die Erde bei 1 AE der im Mittel näheste Planet ist, Venus, Merkur und Sonne sowie Mars und Jupiter sind im Mittel weiter entfernt.
Hallo Tom,
das verwundert mich, zumal die Autoren dieses hier schreiben:
Further, Mercury is the closest neighbor, on average, to each of the other seven planets in the solar system.
Freundliche Grüsse, Ralf
Re: Welcher Planet ist der Erde am nähsten?
Verfasst: 25. Mär 2019, 06:54
von tomS
Ich kann nur auf den Plot verweisen; man sieht ein Minimum bei ca. 1 AE.
Mal ernsthaft: das Ganze ist Spielerei - Theoretische Physik “Mechanik I”. So wird z.B. die Exzentrizität nicht mal diskutiert.
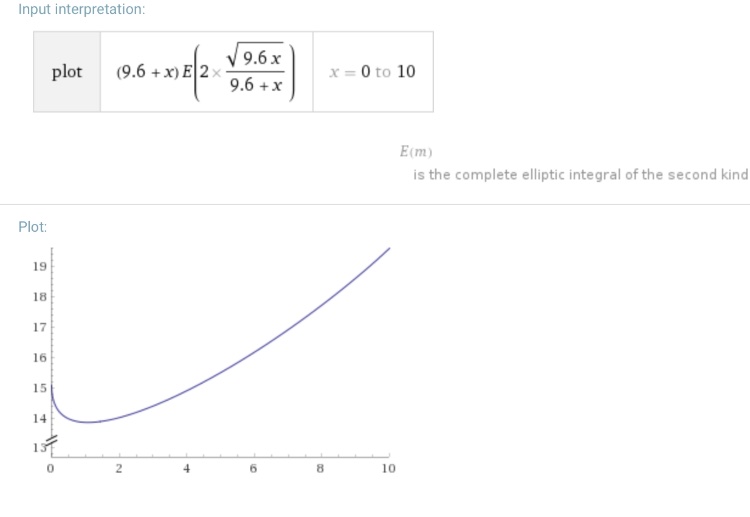
- mean distance Saturn (9.6 AE) to other circular Kepler orbits
- 165AD605-2790-4384-9D94-C74417266B04.jpeg (28.45 KiB) 9881 mal betrachtet
Re: Welcher Planet ist der Erde am nähsten?
Verfasst: 25. Mär 2019, 09:07
von tomS
Ich könnte mich ärgern ...
... weil das Ganze unheimlich trivial ist - Mathematikerwitz - ich die wesentliche Aussage schon im ersten Beitrag dastehen hatte und mich durch irrelevante Details wie Exzentrizität und elliptische Funktionen habe ablenken lassen.
Für den mittleren quadratischen Abstand gilt
D₁₂² = r₁² + r₂²
Setzt man r₂ = const. und lässt r₁ = r variabel, so folgt
D²(r) = r² + const.
D.h. bei festem Bahnradius z.B. der Erde erhält man kleineres mittleres Abstandsquadrat für kleinere Bahnradien.
Re: Welcher Planet ist der Erde am nähsten?
Verfasst: 25. Mär 2019, 09:11
von Frank
tomS hat geschrieben: ↑25. Mär 2019, 09:07
Ich könnte mich ärgern ...
... weil das Ganze unheimlich trivial ist - Mathematikerwitz - ich die wesentliche Aussage schon im ersten Beitrag dastehen hatte und mich durch irrelevante Details wie Exzentrizität und elliptische Funktionen habe ablenken lassen.
Für den mittleren quadratischen Abstand gilt
D₁₂² = r₁² + r₂²
Setzt man r₂ = const. und lässt r₁ = r variabel, so folgt
D²(r) = r² + const.
D.h. bei festem Bahnradius z.B. der Erde erhält man kleineres mittleres Abstandsquadrat für kleinere Bahnradien.
Und das heisst jetzt für den "Normalsterblichen"?
Re: Welcher Planet ist der Erde am nähsten?
Verfasst: 25. Mär 2019, 09:48
von tomS
D.h., dass wenn man für einen Planeten wie die Erde die mittleren Abstandsquadrate der anderen Planeten berechnet, die Planeten mit kleinerem Bahnradius auch kleineres mittleres Abstandsquadrat haben. Umgekehrt: für das mittlere Abstandsquadrat zweier Planeten ist die Differenz der Bahnradien irrelevant.
Re: Welcher Planet ist der Erde am nähsten?
Verfasst: 25. Mär 2019, 10:45
von ralfkannenberg
tomS hat geschrieben: ↑25. Mär 2019, 09:07
Ich könnte mich ärgern ...
Hallo Tom,
warum ?
tomS hat geschrieben: ↑25. Mär 2019, 09:07
... weil das Ganze unheimlich trivial ist - Mathematikerwitz - ich die wesentliche Aussage schon im ersten Beitrag dastehen hatte und mich durch irrelevante Details wie Exzentrizität und elliptische Funktionen habe ablenken lassen.
Vermutlich vor allem von diesen elliptischen Funktionen, die die volle Aufmerksamkeit auf sich ziehen.
tomS hat geschrieben: ↑25. Mär 2019, 09:07
Für den mittleren quadratischen Abstand gilt
D₁₂² = r₁² + r₂²
Setzt man r₂ = const. und lässt r₁ = r variabel, so folgt
D²(r) = r² + const.
D.h. bei festem Bahnradius z.B. der Erde erhält man kleineres mittleres Abstandsquadrat für kleinere Bahnradien.
Auch wenn meine Intuition ein solches Resultat "erhofft" hatte - da ich zum Glück nicht in den "Genuss" (Durchfallrate im Vordiplom bei 50% an der ETH Zürich) der Mechanik I - Vorlesung kam, die mir erlassen wurde, weil ich bei meinem Vordiplom an der Uni Basel das Physikpraktikum für Vorgerückte absolvieren musste, welches ebenfalls rund 50% aller Studierenden "aussiebte", bin ich also mit den entsprechenden Methoden überhaupt nicht vertraut.
Wie auch immer: wie steht dieses Resultat nun zum Saturn-Resultat, dass bei ihm die Erde der durchschnitts-nächste Planet sei ?
Freundliche Grüsse, Ralf
Re: Welcher Planet ist der Erde am nähsten?
Verfasst: 25. Mär 2019, 13:29
von tomS
ralfkannenberg hat geschrieben: ↑25. Mär 2019, 10:45
Wie auch immer: wie steht dieses Resultat nun zum Saturn-Resultat, dass bei ihm die Erde der durchschnitts-nächste Planet sei ?
Der mittlere Abstand hat ein Minimum bei r > 0, im Falle des Saturns bei ca. 1 AE.
Der mittlere quadratische Abstand hat ein Minimum bei r = 0. Das ist auch einsichtig, da die Wurzel des mittleren quadratischeN Abstands der nullten Taylornäherung des mittleren Abstand entspricht.
Re: Welcher Planet ist der Erde am nähsten?
Verfasst: 25. Mär 2019, 14:30
von ralfkannenberg
tomS hat geschrieben: ↑25. Mär 2019, 13:29
mittlere Abstand
(...)
mittlere quadratische Abstand
Hallo Tom,
das heisst, man verwendet
verschiedene Abstandsbegriffe. Man könnte beispielsweise auch den mittleren "kubischen" Abstand verwenden, nicht wahr ?
Aber welcher ist denn nun der "richtige" ? - Insbesondere bin ich nun etwas überrascht, dass die Forenuser die Definition verstanden haben, obgleich es mehrere von denen gibt, die zudem verschiedene Ergebnisse liefern ...
Freundliche Grüsse, Ralf
Re: Welcher Planet ist der Erde am nähsten?
Verfasst: 25. Mär 2019, 16:08
von tomS
Hallo Ralf,
Es ist doch klar, dass die Quadratwurzel des Erwartungswertes des Quadrates des Abstandes etwas anderes liefert als der Erwartungswert des Abstandes.
Welches ist der richtige Abstandsbegriff? Ich würde eher fragen, welches der jeweils nützlichste ist. Im vorliegenden Fall ist jedenfalls der erste der einfachere, da die Quadratwurzel verschwindet - siehe Rechnung auf Astronews.
Re: Welcher Planet ist der Erde am nähsten?
Verfasst: 25. Mär 2019, 17:10
von ralfkannenberg
tomS hat geschrieben: ↑25. Mär 2019, 16:08
Es ist doch klar, dass die
Quadratwurzel des Erwartungswertes des Quadrates des Abstandes etwas anderes liefert als der
Erwartungswert des Abstandes.
Hallo Tom,
natürlich, womit wir auch schon bei den L
p-Räumen bzw. den L
p-Normen sind, wobei p auch den Wert unendlich annehmen kann.
tomS hat geschrieben: ↑25. Mär 2019, 16:08
Welches ist der richtige Abstandsbegriff? Ich würde eher fragen, welches der jeweils nützlichste ist. Im vorliegenden Fall ist jedenfalls der erste der
einfachere, da die Quadratwurzel verschwindet - siehe Rechnung auf Astronews.
Na ja, als "nützlich" würde ich nach wie vor weniger einen der mittleren "aktuellen" Abstände ansehen, sondern den Vergleich der Umlaufbahnen, im Fall der Planeten auf die Grosse Halbachse oder meinetwegen auch die Perihele eingeschränkt, das macht bei den geringen Exzentrizitäten ohnehin fast nichts aus.
Freundliche Grüsse, Ralf


