Hinweis auf die DSGVO: Auf unserer Seite werden keine Dritt-Anbieter-Cookies verwendet und nur Daten erfasst, welche für das Minimum an Board-Funktionalität notwendig sind.
Bevor Sie sich registrieren oder das Board verwenden, lesen Sie bitte zusätzlich die DSGVO-Erklärung, welche in der Navigationsleiste verlinkt ist.
Kurzfassung der unserer Meinung nach wichtigsten DSGVO-Punkte:
Es kann vorkommen, dass Benutzer eigenverantwortlich Videos oder sonstige Medien in ihren Beiträgen verlinken, welche beim Aufruf der Forenseite als Teil der Seite samt zugehörigem Material mitgeladen werden. Sollten Sie dies nicht wünschen, verwenden Sie beim Benutzen des Forums einen Blocker wie z.B. uMatrix, welcher das Laden von Inhaltsblöcken von Fremd-URLs effektiv unterbinden kann.
Wir blenden keine Werbung ein und schränken die Inhalte in keinster Weise bei Benutzung von Addblockern ein. Dadurch ist die Grundfunktionalität des Forums auch bei vollständigem Blockieren von Drittanbieter-Inhalten stets gegeben.
Cookies werden unsererseits nur verwendet um das Einloggen des Benutzers für die Dauer der Forenbenutzung zu speichern. Es steht dem Benutzer frei die Option 'Angemeldet bleiben' zu verwenden, damit der Cookie dauerhaft gespeichert bleibt und beim nächsten Besuch kein erneutes Einloggen mehr notwendig ist.
EMail-Adressen werden für Kontakt bei wichtigen Mitteilungen und zur Widerherstellung des Passwortes verwendet. Die verwendeten IPs können von uns ohne externe Hilfsmittel mit keiner realen Person in Verbindung gebracht werden und werden nach spätestens 7 Tagen gelöscht. Diese IPs werden höchstens verwendet um Neuanmeldungen unerwünschter oder gesperrter Nutzer zu identfizieren und zu unterbinden. Wir behalten uns daher vor bei Verdacht, die Frist für die IP-Löschung auf maximal 14 Tage zu verlängern.
Unsere Webseite läuft auf einem virtuellen Linux-Server, welcher von einem externen Anbieter gehostet wird. Etwaige Verstöße der DSGVO-Auflagen seitens dieses deutschen Hosters können wir nicht feststellen und somit auch nicht verfolgen.
Wir halten Backups unserer Datenbanken, welche in regelmäßigen Abständen als Schutz vor Katastrophen, Hackerangriffen und sonstigen Ausfällen erstellt werden. Sollte ein Nutzer die Löschung seiner Daten wünschen, betrachten wir es als Unzumutbar die Backups auch von den Daten zu befreien, da es sich hierbei um eine mehrtägiges Unterfangen handelt - dies ist für eine Einzelperson beim Betrieb eines privaten Forums nicht zumutbar möglich ohne das Backup komplett zu löschen.
Sollten Sie etwas gegen die dauerhafte anonyme Speicherung ihrer EMail-Adresse, ihres Pseudonyms und ihrer Beiträge in einem Backup haben, sehen Sie von der Registrierung in diesem Forum ab. Für Mitglieder, welche vor dem 25.05.2018 registriert waren steht jedoch das Recht im Raum, eine Löschung der Datenbank-Backups zu beantragen.
Wenn dies Ihr erster Besuch hier ist, lesen Sie bitte zunächst die FAQs sowie die wesentlichen Regeln zur Benutzung des Forums.
Um an den Diskussionen teilnehmen zu können, müssen Sie sich zunächst registrieren.
Bevor Sie sich registrieren oder das Board verwenden, lesen Sie bitte zusätzlich die DSGVO-Erklärung, welche in der Navigationsleiste verlinkt ist.
Kurzfassung der unserer Meinung nach wichtigsten DSGVO-Punkte:
Es kann vorkommen, dass Benutzer eigenverantwortlich Videos oder sonstige Medien in ihren Beiträgen verlinken, welche beim Aufruf der Forenseite als Teil der Seite samt zugehörigem Material mitgeladen werden. Sollten Sie dies nicht wünschen, verwenden Sie beim Benutzen des Forums einen Blocker wie z.B. uMatrix, welcher das Laden von Inhaltsblöcken von Fremd-URLs effektiv unterbinden kann.
Wir blenden keine Werbung ein und schränken die Inhalte in keinster Weise bei Benutzung von Addblockern ein. Dadurch ist die Grundfunktionalität des Forums auch bei vollständigem Blockieren von Drittanbieter-Inhalten stets gegeben.
Cookies werden unsererseits nur verwendet um das Einloggen des Benutzers für die Dauer der Forenbenutzung zu speichern. Es steht dem Benutzer frei die Option 'Angemeldet bleiben' zu verwenden, damit der Cookie dauerhaft gespeichert bleibt und beim nächsten Besuch kein erneutes Einloggen mehr notwendig ist.
EMail-Adressen werden für Kontakt bei wichtigen Mitteilungen und zur Widerherstellung des Passwortes verwendet. Die verwendeten IPs können von uns ohne externe Hilfsmittel mit keiner realen Person in Verbindung gebracht werden und werden nach spätestens 7 Tagen gelöscht. Diese IPs werden höchstens verwendet um Neuanmeldungen unerwünschter oder gesperrter Nutzer zu identfizieren und zu unterbinden. Wir behalten uns daher vor bei Verdacht, die Frist für die IP-Löschung auf maximal 14 Tage zu verlängern.
Unsere Webseite läuft auf einem virtuellen Linux-Server, welcher von einem externen Anbieter gehostet wird. Etwaige Verstöße der DSGVO-Auflagen seitens dieses deutschen Hosters können wir nicht feststellen und somit auch nicht verfolgen.
Wir halten Backups unserer Datenbanken, welche in regelmäßigen Abständen als Schutz vor Katastrophen, Hackerangriffen und sonstigen Ausfällen erstellt werden. Sollte ein Nutzer die Löschung seiner Daten wünschen, betrachten wir es als Unzumutbar die Backups auch von den Daten zu befreien, da es sich hierbei um eine mehrtägiges Unterfangen handelt - dies ist für eine Einzelperson beim Betrieb eines privaten Forums nicht zumutbar möglich ohne das Backup komplett zu löschen.
Sollten Sie etwas gegen die dauerhafte anonyme Speicherung ihrer EMail-Adresse, ihres Pseudonyms und ihrer Beiträge in einem Backup haben, sehen Sie von der Registrierung in diesem Forum ab. Für Mitglieder, welche vor dem 25.05.2018 registriert waren steht jedoch das Recht im Raum, eine Löschung der Datenbank-Backups zu beantragen.
Wenn dies Ihr erster Besuch hier ist, lesen Sie bitte zunächst die FAQs sowie die wesentlichen Regeln zur Benutzung des Forums.
Um an den Diskussionen teilnehmen zu können, müssen Sie sich zunächst registrieren.
QM-Frage-Antwort
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: QM-Frage-Antwort
Meine fehlende Mathematik-Ausbildung wieder mal  : Lässt sich jede Lösung der Schrödingergleichung und auch die der anderen Bewegungsgleichungen der QM/QFT durch ebene Wellen ausdrücken? Auch die gebundener Zustände, unter Berücksichtigung der Potentiale natürlich?
: Lässt sich jede Lösung der Schrödingergleichung und auch die der anderen Bewegungsgleichungen der QM/QFT durch ebene Wellen ausdrücken? Auch die gebundener Zustände, unter Berücksichtigung der Potentiale natürlich?
Re: QM-Frage-Antwort
Mathematisch gesehen im Prinzip ja: per Fourier-Analyse lässt sich jede Funktion in ein kontinuierliches Spektrum ebener Wellen zerlegen, z.B. http://de.wikipedia.org/wiki/Fourier-Transformationpositronium hat geschrieben:Meine fehlende Mathematik-Ausbildung wieder mal: Lässt sich jede Lösung der Schrödingergleichung und auch die der anderen Bewegungsgleichungen der QM/QFT durch ebene Wellen ausdrücken? Auch die gebundener Zustände, unter Berücksichtigung der Potentiale natürlich?
In der Physik sind ebene Wellen die Energie-Eigenzustände zu freien Teilchen; bei gebundenen Problemen z.B. empfehlen sie sich nicht wirklich als Basisvektoren.
Bei Streuproblemen sind sie auch sehr nützlich: man approximiert die ein- und auslaufenden Teilchen in großer Entfernung von Streuzentrum als ebene Wellen.
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: QM-Frage-Antwort
Vielen Dank für Deine Antwort!
Müsste man demnach zur Darstellung durch ebene Wellen so vorgehen, dass man (stehende) Ebene Wellen aus allen Raumrichtungen additiv überlagert, durch das Potential gewichtet und normiert?
Dass man Atomorbitale in Radial- und Kugelflächenfunktionen zerlegt statt eine Überlagerung ebener Wellen zu verwenden ist also rein durch rechentechnisch praktischeres Vorgehen begründet?Hawkwind hat geschrieben:...bei gebundenen Problemen z.B. empfehlen sie sich nicht wirklich als Basisvektoren.
Müsste man demnach zur Darstellung durch ebene Wellen so vorgehen, dass man (stehende) Ebene Wellen aus allen Raumrichtungen additiv überlagert, durch das Potential gewichtet und normiert?
Re: QM-Frage-Antwort
Man löst ein Eigenwertproblem, sucht Eigenfunktionen und v.a. Eigenwerte des Hamilton-Operators. Diese Eigenfunktionen haben eine scharfe Energie (eben die Eigenwerte). Beim Wasserstoffatom ergeben sich als Eigenfunktionen die von dir geschilderten Funktionen. Sie dienen als Basis-Zustände für die Erzeugung allgemeiner Lösungen desselben Problems via Linearkombination über diese Basiszustände; diese allgemeinen Lösungen haben dann i.a. keine scharfen Energien mehr.positronium hat geschrieben:Vielen Dank für Deine Antwort!
Dass man Atomorbitale in Radial- und Kugelflächenfunktionen zerlegt statt eine Überlagerung ebener Wellen zu verwenden ist also rein durch rechentechnisch praktischeres Vorgehen begründet?Hawkwind hat geschrieben:...bei gebundenen Problemen z.B. empfehlen sie sich nicht wirklich als Basisvektoren.
Ebene Wellen ergeben sich nicht als Lösungen des Wasserstoffatom-Problems, aber man könnte die gefundenen Eigenfunktionen als Fourierintegrale darstellen. Ich wüsste nur spontan nicht, wozu man so etwas machen sollte.
Denke nicht, du müsstet "einfach" die Fourier-Integrale lösen, d.h.positronium hat geschrieben: Müsste man demnach zur Darstellung durch ebene Wellen so vorgehen, dass man (stehende) Ebene Wellen aus allen Raumrichtungen additiv überlagert, durch das Potential gewichtet und normiert?

das natürlich in 3 Dimensionen und für f(x) die gefunden Lösungen des Wasserstoffatom-problems einsetzen (die Eigenfunktionen). Dann bekämst du pro Eigenfunktion deren spektrale (kontinuierliche) Zerlegung in ebene Wellen.
___
Formel geborgt aus http://de.wikipedia.org/wiki/Fourier-Transformation
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: QM-Frage-Antwort
Es geht mir darum, die Schrödingergleichung zu verstehen, und sie nicht nur hinzunehmen und zu berechnen. Die SG ist ja schliesslich nur eine Bewegungsgleichung, aber für was bzw. genauer: welche Eigenschaften hat dieses "Objekt", auf welches sie wirkt? Und um die Fragestellung zu vertiefen: Wie viel der SG gehört in Wirklichkeit sogar noch zu diesem "Objekt"?Hawkwind hat geschrieben:Ebene Wellen ergeben sich nicht als Lösungen des Wasserstoffatom-Problems, aber man könnte die gefundenen Eigenfunktionen als Fourierintegrale darstellen. Ich wüsste nur spontan nicht, wozu man so etwas machen sollte.
Beim freien Teilchen liegt als reales Objekt in etwa so etwas wie eine Überlagerung ebener Wellen vor. Jetzt ist meine Vermutung, dass das auch beim gebundenen Zustand ohne grossartige Änderungen der Fall sein sollte (beim harmonischen Oszillator ohne Drehimpuls ist das ja auch so); es müsste also Forderungen an das Objekt geben, welche dieses einerseits im Potential zu dem macht, was die Orbitale liefert, und andererseits im freien Fall vom freien Wellenpaket ununterscheidbar lässt. Eine Eigenschaft ist natürlich, dass die Zustände stationär sein müssen. Vielleicht ist das der einzige wirkliche Unterschied.
Um das zu verstehen ist es eben nicht ausreichend die "normale" Lösung des Wasserstoffproblems zu betrachten, sondern die Grundlagen zu erkennen. Von daher meine Frage, ob sich jeder Zustand prinzipiell durch ebene Wellen beschreiben lässt. Du schreibst ja, aber das ist wohl zu kompliziert. Ich dachte halt ganz naiv: Nehme ich ein freies Wellenpaket, nagele das in der Mitte fest und schaue, dass die Teilwellen aussen nicht zappeln. Eigentlich müssten doch die Zustände ohne Drehimpuls so darstellbar sein. Aber der Drehimpuls macht das wohl schwierig.
Re: QM-Frage-Antwort
Nur hierzu:
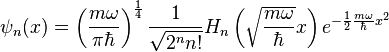
aus
http://de.wikipedia.org/wiki/Harmonisch ... echanik%29
und auch nicht leicht in ebene Wellen zerlegbar (höchstens über das ewrähnte Fourier-Integral).
Du verwechselst das vielleicht mit dem Kasten-Potential-Problem der Quantenmechanik (http://de.wikipedia.org/wiki/Kastenpotential); dort sind die Lösungen stehende Wellen, die man ja als Überlagerung 2er in entgegengesetzten Richtungen propagierenden ebenen Wellen darstellen kann.
Nein, die Eigenzustände beim harmonischen Oszillator in der Quantenmechanik sind keine ebenen Wellen:positronium hat geschrieben: ...
Beim freien Teilchen liegt als reales Objekt in etwa so etwas wie eine Überlagerung ebener Wellen vor. Jetzt ist meine Vermutung, dass das auch beim gebundenen Zustand ohne grossartige Änderungen der Fall sein sollte (beim harmonischen Oszillator ohne Drehimpuls ist das ja auch so);
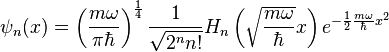
aus
http://de.wikipedia.org/wiki/Harmonisch ... echanik%29
und auch nicht leicht in ebene Wellen zerlegbar (höchstens über das ewrähnte Fourier-Integral).
Du verwechselst das vielleicht mit dem Kasten-Potential-Problem der Quantenmechanik (http://de.wikipedia.org/wiki/Kastenpotential); dort sind die Lösungen stehende Wellen, die man ja als Überlagerung 2er in entgegengesetzten Richtungen propagierenden ebenen Wellen darstellen kann.
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: QM-Frage-Antwort
Oh, ja. Danke.Hawkwind hat geschrieben:Nein, die Eigenzustände beim harmonischen Oszillator in der Quantenmechanik sind keine ebenen Wellen:
Der Unterschied dieser Funktion im Vergleich zur ebenen Welle sollte aber nur durch die Potentialfunktion und die Stationärität entstehen...
Dann sollte ich meine Eingangsfrage anders formulieren: Kann man jede Lösung der SG etc. durch Funktionen f darstellen? Eine mathematisch korrekte Bezeichnung für das, was ich mir unter f vorstelle, kenne ich nicht; ich meine damit schwingende Funktionen, die "geradlinig" verlaufen. Mit geradlinig meine ich, dass die Wellenmaxima bei konstantem Potential stets die gleichen Abstände haben und in der gleichen Richtung liegen - bei den Kugelflächenfunktionen ist ja das nicht der Fall.
Re: QM-Frage-Antwort
Ja, kann man.
Die SGL ist auf dem Abschluss des Hilbertraumes der quadratintegrablen Funktionen definiert, d.h. jede Lösung ist eine geeignete Funktion von x und t.
Die SGL ist auf dem Abschluss des Hilbertraumes der quadratintegrablen Funktionen definiert, d.h. jede Lösung ist eine geeignete Funktion von x und t.
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: QM-Frage-Antwort
Vielen Dank für Deine Antwort!
Bis zu
Bis zu
verstehe ich das, aber ab hier nicht mehr so recht.tomS hat geschrieben:Ja, kann man.
Bedeutet das "Abschluss", dass jedes Ergebnis aus nur von einer räumlichen Koordinate abhängigen Funktionen (also, x steht nur für x, nicht für {x,y,z}) zusammengesetzt ist? - Das würde ja dem "geradlinig" entsprechen.tomS hat geschrieben:Die SGL ist auf dem Abschluss des Hilbertraumes der quadratintegrablen Funktionen definiert, d.h. jede Lösung ist eine geeignete Funktion von x und t.
Re: QM-Frage-Antwort
Quadratintegrabel bedeutet, dass das Integral

existiert.
Für ebene Wellen existiert dieses Integral nicht, allerdings kann man diese als Grenzübergang aus quadratintegrablen Funktionen ableiten. Dies nennt man Abschluss.
existiert.
Für ebene Wellen existiert dieses Integral nicht, allerdings kann man diese als Grenzübergang aus quadratintegrablen Funktionen ableiten. Dies nennt man Abschluss.
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: QM-Frage-Antwort
Heisst das, dass in Wirklichkeit alles auch aus quadratintegrablen Funktionen konstruiert werden kann, und nicht umgekehrt, wie ich oben gefragt habe? Ich sehe jetzt aber nicht, warum solche Funktionen automatisch meine obigen Bedingungen erfüllen sollten.tomS hat geschrieben:...allerdings kann man diese als Grenzübergang aus quadratintegrablen Funktionen ableiten. Dies nennt man Abschluss.
Re: QM-Frage-Antwort
Dass quadratintegrable Funktionen verwendet werden ist eine Folge dessen, dass man eine Wahrscheinlichkeitsdichte einführen möchte. Dies kann als ein Axiom der QM angesehen werden.
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: QM-Frage-Antwort
Ja, schon.
Ich bin mir nicht sicher, ob ich meine Frage verständlich herüber bringen konnte.
Vielleicht besser so: Sind alle Zustände durch Wellenfunktionen beschreibbar, deren Wellenfronten stets parallel verlaufen, es sei denn, das Potential verändert die Geschwindigkeit und damit je nach Ort die Frequenz? Kann man vom Prinzip auch ohne Kugelwellen, Kugelflächenfunktionen und dergleichen alles formulieren?
Ich bin mir nicht sicher, ob ich meine Frage verständlich herüber bringen konnte.
Vielleicht besser so: Sind alle Zustände durch Wellenfunktionen beschreibbar, deren Wellenfronten stets parallel verlaufen, es sei denn, das Potential verändert die Geschwindigkeit und damit je nach Ort die Frequenz? Kann man vom Prinzip auch ohne Kugelwellen, Kugelflächenfunktionen und dergleichen alles formulieren?
Re: QM-Frage-Antwort
I.A. kannst du über du Form der Wellenfunktionen nichts sagen. Aber eine Zerlegung nach Orthonormalsystemem ist immer möglich.
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: QM-Frage-Antwort
OK. Vielen Dank!
Re: QM-Frage-Antwort
Ach ja, und die Lösung der SGL, d.h. die Eigenfunktionen des Hamiltonoperators stellen immer ein Orthonormalsystem dar.
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: QM-Frage-Antwort
Lassen sich die Ursachen der natürlichen/homogenen Linienbreite vollständig auf Störungen und Ungenauigkeiten der Messapparatur zurückführen, oder könnte da noch ein wesentlicher Teil z.B. auf leicht variable Bindungsenergien (etwa Energieniveaus im Wasserstoffatom) zurückführbar sein?
Re: QM-Frage-Antwort
Folgt die Linienbreite nicht einfach via Unschärferelation aus der endlichen Lebensdauer des Zustands?
Linienbreite
Linienbreite
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: QM-Frage-Antwort
Ich habe den Eindruck, dass das nur in manchen Fällen und zum Teil so ist. Auf dieser Wikipedia-Seite steht: "Nach der Quantenmechanik kann ein physikalisches System, wenn es eine scharf definierte Energie besitzt, sich zeitlich nicht verändern. Systeme, die spontan zerfallen oder eine Strahlung erzeugen, besitzen daher eine prinzipielle Energieunschärfe..." Wenn ich das richtig verstehe, bezieht sich das z.B. auf Tunneleffekte, so dass dabei einmal etwas mehr, einmal etwas weniger Energie über die Barriere mitkommt. Aber gebundene Elektronen stellen ja keinen instabilen Zustand dar, und besitzen eine feste Energie. Und eigentlich entwickelt sich so ein Zustand auch gar nicht, sondern es wird nur die Phase der Wellen verschoben.Hawkwind hat geschrieben:Folgt die Linienbreite nicht einfach via Unschärferelation aus der endlichen Lebensdauer des Zustands?
Linienbreite
Re: QM-Frage-Antwort
Mal abgesehen vom Grundzustand sind das doch alles angeregte Zustände mit endlicher Lebensdauer und daher mit einer Breite > 0.positronium hat geschrieben:Aber gebundene Elektronen stellen ja keinen instabilen Zustand dar, und besitzen eine feste Energie.
Re: QM-Frage-Antwort
Hinzu kommt, dass die beobachteten Teilchen eine Temperatur haben, also ungeordnet schwingen.
Das sorgt für eine weitere Linienverbreiterung (Dopplereffekt, Stoß-Wechselwirkungen).
Grüße
seeker
Das sorgt für eine weitere Linienverbreiterung (Dopplereffekt, Stoß-Wechselwirkungen).
Grüße
seeker
Grüße
seeker
Wissenschaft ... ist die Methode, kühne Hypothesen aufstellen und sie der schärfsten Kritik auszusetzen, um herauszufinden, wo wir uns geirrt haben.
Karl Popper
seeker
Wissenschaft ... ist die Methode, kühne Hypothesen aufstellen und sie der schärfsten Kritik auszusetzen, um herauszufinden, wo wir uns geirrt haben.
Karl Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: QM-Frage-Antwort
Ja, Du hast Recht. Jetzt ordnet sich das gerade bei mir. Man muss sich den Zustandsübergang soz. auch als eine Schwingung vorstellen. Und die Übergangswahrscheinlichkeit in alle Zustände spielt eine Rolle, sodass bei gebundenen Elektronen es auch eine Rolle spielt, wie viele innere Zustände besetzt sind... Danke!Hawkwind hat geschrieben:Mal abgesehen vom Grundzustand sind das doch alles angeregte Zustände mit endlicher Lebensdauer und daher mit einer Breite > 0.positronium hat geschrieben:Aber gebundene Elektronen stellen ja keinen instabilen Zustand dar, und besitzen eine feste Energie.
Re: QM-Frage-Antwort
Die QM hat da etwas Probleme, das exakt zu beschreiben, weil sie kein Photon kennt; stattdessen behilft man sich mit einem äußeren Feld. In der QED würde man dagegen ein Übergangsmatrixelement
<A*|U(t)|A,gamma>
U(t) = exp(-iHt)
berechnen
<A*|U(t)|A,gamma>
U(t) = exp(-iHt)
berechnen
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: QM-Frage-Antwort
Vielen Dank, seeker und Tom!
Folgt daraus dann ganz selbstverständlich eine Energieverteilung?tomS hat geschrieben:In der QED würde man dagegen ein Übergangsmatrixelement
<A*|U(t)|A,gamma>
U(t) = exp(-iHt)
berechnen
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: QM-Frage-Antwort
Hallo,
man kann ja die zeitunabhängige SG so umschreiben:
=\frac{\partial ^2\psi (x)}{\partial x^2})
Spricht etwas dagegen (oder dafür), darin das v nicht mit dem m als Impuls zu betrachten, sondern bereits als Teil der SRT? Dann wären also Wellen nicht p-abhängig, sondern abhängig von einer m- bzw. m*gamma-Welle, deren Phasenverschiebung 1/v beträgt, bzw. würde eben die Relativität der Gleichzeitigkeit in bewegten Systemen widerspiegeln.
Gruss
positronium
man kann ja die zeitunabhängige SG so umschreiben:
Spricht etwas dagegen (oder dafür), darin das v nicht mit dem m als Impuls zu betrachten, sondern bereits als Teil der SRT? Dann wären also Wellen nicht p-abhängig, sondern abhängig von einer m- bzw. m*gamma-Welle, deren Phasenverschiebung 1/v beträgt, bzw. würde eben die Relativität der Gleichzeitigkeit in bewegten Systemen widerspiegeln.
Gruss
positronium
