Hinweis auf die DSGVO: Auf unserer Seite werden keine Dritt-Anbieter-Cookies verwendet und nur Daten erfasst, welche für das Minimum an Board-Funktionalität notwendig sind.
Bevor Sie sich registrieren oder das Board verwenden, lesen Sie bitte zusätzlich die DSGVO-Erklärung, welche in der Navigationsleiste verlinkt ist.
Kurzfassung der unserer Meinung nach wichtigsten DSGVO-Punkte:
Es kann vorkommen, dass Benutzer eigenverantwortlich Videos oder sonstige Medien in ihren Beiträgen verlinken, welche beim Aufruf der Forenseite als Teil der Seite samt zugehörigem Material mitgeladen werden. Sollten Sie dies nicht wünschen, verwenden Sie beim Benutzen des Forums einen Blocker wie z.B. uMatrix, welcher das Laden von Inhaltsblöcken von Fremd-URLs effektiv unterbinden kann.
Wir blenden keine Werbung ein und schränken die Inhalte in keinster Weise bei Benutzung von Addblockern ein. Dadurch ist die Grundfunktionalität des Forums auch bei vollständigem Blockieren von Drittanbieter-Inhalten stets gegeben.
Cookies werden unsererseits nur verwendet um das Einloggen des Benutzers für die Dauer der Forenbenutzung zu speichern. Es steht dem Benutzer frei die Option 'Angemeldet bleiben' zu verwenden, damit der Cookie dauerhaft gespeichert bleibt und beim nächsten Besuch kein erneutes Einloggen mehr notwendig ist.
EMail-Adressen werden für Kontakt bei wichtigen Mitteilungen und zur Widerherstellung des Passwortes verwendet. Die verwendeten IPs können von uns ohne externe Hilfsmittel mit keiner realen Person in Verbindung gebracht werden und werden nach spätestens 7 Tagen gelöscht. Diese IPs werden höchstens verwendet um Neuanmeldungen unerwünschter oder gesperrter Nutzer zu identfizieren und zu unterbinden. Wir behalten uns daher vor bei Verdacht, die Frist für die IP-Löschung auf maximal 14 Tage zu verlängern.
Unsere Webseite läuft auf einem virtuellen Linux-Server, welcher von einem externen Anbieter gehostet wird. Etwaige Verstöße der DSGVO-Auflagen seitens dieses deutschen Hosters können wir nicht feststellen und somit auch nicht verfolgen.
Wir halten Backups unserer Datenbanken, welche in regelmäßigen Abständen als Schutz vor Katastrophen, Hackerangriffen und sonstigen Ausfällen erstellt werden. Sollte ein Nutzer die Löschung seiner Daten wünschen, betrachten wir es als Unzumutbar die Backups auch von den Daten zu befreien, da es sich hierbei um eine mehrtägiges Unterfangen handelt - dies ist für eine Einzelperson beim Betrieb eines privaten Forums nicht zumutbar möglich ohne das Backup komplett zu löschen.
Sollten Sie etwas gegen die dauerhafte anonyme Speicherung ihrer EMail-Adresse, ihres Pseudonyms und ihrer Beiträge in einem Backup haben, sehen Sie von der Registrierung in diesem Forum ab. Für Mitglieder, welche vor dem 25.05.2018 registriert waren steht jedoch das Recht im Raum, eine Löschung der Datenbank-Backups zu beantragen.
Wenn dies Ihr erster Besuch hier ist, lesen Sie bitte zunächst die FAQs sowie die wesentlichen Regeln zur Benutzung des Forums.
Um an den Diskussionen teilnehmen zu können, müssen Sie sich zunächst registrieren.
Bevor Sie sich registrieren oder das Board verwenden, lesen Sie bitte zusätzlich die DSGVO-Erklärung, welche in der Navigationsleiste verlinkt ist.
Kurzfassung der unserer Meinung nach wichtigsten DSGVO-Punkte:
Es kann vorkommen, dass Benutzer eigenverantwortlich Videos oder sonstige Medien in ihren Beiträgen verlinken, welche beim Aufruf der Forenseite als Teil der Seite samt zugehörigem Material mitgeladen werden. Sollten Sie dies nicht wünschen, verwenden Sie beim Benutzen des Forums einen Blocker wie z.B. uMatrix, welcher das Laden von Inhaltsblöcken von Fremd-URLs effektiv unterbinden kann.
Wir blenden keine Werbung ein und schränken die Inhalte in keinster Weise bei Benutzung von Addblockern ein. Dadurch ist die Grundfunktionalität des Forums auch bei vollständigem Blockieren von Drittanbieter-Inhalten stets gegeben.
Cookies werden unsererseits nur verwendet um das Einloggen des Benutzers für die Dauer der Forenbenutzung zu speichern. Es steht dem Benutzer frei die Option 'Angemeldet bleiben' zu verwenden, damit der Cookie dauerhaft gespeichert bleibt und beim nächsten Besuch kein erneutes Einloggen mehr notwendig ist.
EMail-Adressen werden für Kontakt bei wichtigen Mitteilungen und zur Widerherstellung des Passwortes verwendet. Die verwendeten IPs können von uns ohne externe Hilfsmittel mit keiner realen Person in Verbindung gebracht werden und werden nach spätestens 7 Tagen gelöscht. Diese IPs werden höchstens verwendet um Neuanmeldungen unerwünschter oder gesperrter Nutzer zu identfizieren und zu unterbinden. Wir behalten uns daher vor bei Verdacht, die Frist für die IP-Löschung auf maximal 14 Tage zu verlängern.
Unsere Webseite läuft auf einem virtuellen Linux-Server, welcher von einem externen Anbieter gehostet wird. Etwaige Verstöße der DSGVO-Auflagen seitens dieses deutschen Hosters können wir nicht feststellen und somit auch nicht verfolgen.
Wir halten Backups unserer Datenbanken, welche in regelmäßigen Abständen als Schutz vor Katastrophen, Hackerangriffen und sonstigen Ausfällen erstellt werden. Sollte ein Nutzer die Löschung seiner Daten wünschen, betrachten wir es als Unzumutbar die Backups auch von den Daten zu befreien, da es sich hierbei um eine mehrtägiges Unterfangen handelt - dies ist für eine Einzelperson beim Betrieb eines privaten Forums nicht zumutbar möglich ohne das Backup komplett zu löschen.
Sollten Sie etwas gegen die dauerhafte anonyme Speicherung ihrer EMail-Adresse, ihres Pseudonyms und ihrer Beiträge in einem Backup haben, sehen Sie von der Registrierung in diesem Forum ab. Für Mitglieder, welche vor dem 25.05.2018 registriert waren steht jedoch das Recht im Raum, eine Löschung der Datenbank-Backups zu beantragen.
Wenn dies Ihr erster Besuch hier ist, lesen Sie bitte zunächst die FAQs sowie die wesentlichen Regeln zur Benutzung des Forums.
Um an den Diskussionen teilnehmen zu können, müssen Sie sich zunächst registrieren.
Einführung in die Quantenmechanik - Übungen
Re: Einführung in die Quantenmechanik - Übungen
Gar nicht umschreiben, einfach rechnen lassen.
Wertebereiche:
n = 0,1,2,...
z beliebig in C
x beliebig in R
Alternativ die Gleichung a|z> = z|z> in Ortsdarstellung lösen und die resultierende Funktion plotten (siehe der zweite Wikipedia-Link)
Wertebereiche:
n = 0,1,2,...
z beliebig in C
x beliebig in R
Alternativ die Gleichung a|z> = z|z> in Ortsdarstellung lösen und die resultierende Funktion plotten (siehe der zweite Wikipedia-Link)
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: Einführung in die Quantenmechanik - Übungen
Jetzt habe ich mir den "Spass" gegönnt (Das ist vielleicht ein Gerät.  ), den Kommutator auf eine Funktion Psi anzuwenden und zu lösen:
), den Kommutator auf eine Funktion Psi anzuwenden und zu lösen:

Das Ergebnis lautet
\Psi)
Und damit: i[p,x].
Wenn [x,p]=i, dann ist [p,x]=-[x,p]=-i.
Das ergibt dann i*-i=1.
Das Ergebnis lautet
Und damit: i[p,x].
Wenn [x,p]=i, dann ist [p,x]=-[x,p]=-i.
Das ergibt dann i*-i=1.
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: Einführung in die Quantenmechanik - Übungen
Geht leider nicht.
Für

bekomme ich
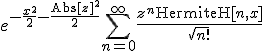
Ohne das sqrt

wird

errechnet.
Dass das sqrt bei der Umwandlung von einer Summe in eine e-Funktion nicht geht, hatte ich schon einmal. Keine Ahnung, warum das so ist.
Für
bekomme ich
Ohne das sqrt
wird
errechnet.
Dass das sqrt bei der Umwandlung von einer Summe in eine e-Funktion nicht geht, hatte ich schon einmal. Keine Ahnung, warum das so ist.
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: Einführung in die Quantenmechanik - Übungen
Wie das mit der Ortsdarstellung funktioniert, weiss ich noch nicht.tomS hat geschrieben:Alternativ die Gleichung a|z> = z|z> in Ortsdarstellung lösen und die resultierende Funktion plotten (siehe der zweite Wikipedia-Link)
Ich schaue mir morgen die Links genauer an - beim reinschauen habe ich jetzt nichts verstanden.
Re: Einführung in die Quantenmechanik - Übungen
Ahh, sorry mein Fehler. Aber für die von mir genannten Fälle, sollte er dann trotzdem 0 ergeben und deine Frage zumindest stückweise beantworten.positronium hat geschrieben:Schaue 3 Posts weiter oben. Dort rechnet Tom das vor:
Der Kommutator ergibt 1.
Kannst du das bitte mal erklären. Vielleicht sollte ich das auch schon wissen, aber im Skript bin ich grad erst bei Kapitel 3 und diese Woche kam mein Buch über Quantum Mechanics von Shankar mit den ich gerade arbeite (aber trotzdem in diesen Thread mit guge - 2 Skript/Buch-Quellen sind besser als eine ;D)tomS hat geschrieben:Und dass der Kommutator 1 ergbt, folgt speziell aus [x,p] = i.
Kommt drauf an , ich arbeite grad in meiner Masterthesis mit Mathematica ;D, aber das Thema ist doch etwas anderstomS hat geschrieben:hat hier jemand Erfahung mit Mathematica o.ä.?
Gerade zu spät um darüber zu gugen und ehrlich gesagt blicke ich grad noch nicht durch was du von positronium/uns willst....
Re: Einführung in die Quantenmechanik - Übungen
Es geht ja um die Berechnung der Ortsdarstellung der kohärenten Zustände z, also umpositronium hat geschrieben:Wie das mit der Ortsdarstellung funktioniert, weiss ich noch nicht.tomS hat geschrieben:Alternativ die Gleichung a|z> = z|z> in Ortsdarstellung lösen und die resultierende Funktion plotten (siehe der zweite Wikipedia-Link)
Man kann auch sofort die Ortsdarstellung von a betrachten, also
und nun die DGL
für quadratintegrable Funktionen lösen (dazu braucht man noch nicht Mathematica, steht im Wikipedia-Link, aber natürlich wieder zum plotten)
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Re: Einführung in die Quantenmechanik - Übungen
Die allgemeinsten Zustände, die in dem Umfeld (z.B. Quantenoptik) interessant sind, sind die sogenannten squeezed states; sie erfüllen ebenfalls
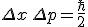
http://en.wikipedia.org/wiki/Squeezed_coherent_state
http://en.wikipedia.org/wiki/Squeezed_coherent_state
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: Einführung in die Quantenmechanik - Übungen
ergibt
Ich setze die Integrationskonstante gleich 1; daraus folgt eine Funktion Psi
(Die Parameter x und z sollen jeweils von einem Unterstrich gefolgt sein - klappt hier in dem tex-Tag leider nicht.)
Plotten mit Plot3D für x [-2..2] und z [-2..2]:
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: Einführung in die Quantenmechanik - Übungen
Wie bzw. warum funktioniert das?
})
ist doch gleich
})
Aber die unendliche Summe für H führt doch zu
})
Dann käme doch
})
heraus?
Oder spielt hier die Wurzel im Nenner nach dem Summenzeichen eine Rolle?
tomS hat geschrieben:
ist doch gleich
Aber die unendliche Summe für H führt doch zu
Dann käme doch
heraus?
Oder spielt hier die Wurzel im Nenner nach dem Summenzeichen eine Rolle?
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: Einführung in die Quantenmechanik - Übungen
Ja, dann sind die Operatoren kommutativ, und das Ergebnis 0.rick hat geschrieben:Aber für die von mir genannten Fälle, sollte er dann trotzdem 0 ergeben und deine Frage zumindest stückweise beantworten.
Ich hätte das doch gleich durchrechnen sollen, hab's aber gescheut, weil die Rechnungen so lang werden.
Re: Einführung in die Quantenmechanik - Übungen
Es funktioniert nicht - es war ein Schreibfehler und musspositronium hat geschrieben:Wie bzw. warum funktioniert das?tomS hat geschrieben: = e^{-x^2/2 H_n(x)})
heißen - sorry!
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: Einführung in die Quantenmechanik - Übungen
Ich habe es mit
)
noch einmal versucht, und dabei die Summe mit der numerischen Funktion NSum gebildet. Für NSum gibt es verschiedene Möglichkeiten für "Method". Je nach Method und Parameter für x und z erfolgt die Berechnung einmal schnell (nur für spezielle x und z), einmal so langsam, dass es keinen Sinn macht, das weiter laufen zu lassen (der Plot braucht ja noch vielfach länger) und in manchen Konfigurationen bekomme ich die Meldung, dass die Summe nicht konvergiert.
Ich glaube, es gibt nur die Möglichkeit, den Ausdruck umzuschreiben (falls das überhaupt geht), damit die Summe in eine Exponentialfunktion umgewandelt werden kann.
noch einmal versucht, und dabei die Summe mit der numerischen Funktion NSum gebildet. Für NSum gibt es verschiedene Möglichkeiten für "Method". Je nach Method und Parameter für x und z erfolgt die Berechnung einmal schnell (nur für spezielle x und z), einmal so langsam, dass es keinen Sinn macht, das weiter laufen zu lassen (der Plot braucht ja noch vielfach länger) und in manchen Konfigurationen bekomme ich die Meldung, dass die Summe nicht konvergiert.
Ich glaube, es gibt nur die Möglichkeit, den Ausdruck umzuschreiben (falls das überhaupt geht), damit die Summe in eine Exponentialfunktion umgewandelt werden kann.
Re: Einführung in die Quantenmechanik - Übungen
Evtl. konvergiert die Summe so besserpositronium hat geschrieben:Ich habe es mit
noch einmal versucht, und dabei die Summe mit der numerischen Funktion NSum gebildet. Für NSum gibt es verschiedene Möglichkeiten für "Method". Je nach Method und Parameter für x und z erfolgt die Berechnung einmal schnell (nur für spezielle x und z), einmal so langsam, dass es keinen Sinn macht, das weiter laufen zu lassen (der Plot braucht ja noch vielfach länger) und in manchen Konfigurationen bekomme ich die Meldung, dass die Summe nicht konvergiert.
Ich glaube, es gibt nur die Möglichkeit, den Ausdruck umzuschreiben (falls das überhaupt geht), damit die Summe in eine Exponentialfunktion umgewandelt werden kann.
Aber wahrscheinlich ist die Methode über die DGL wesentlich effizienter
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: Einführung in die Quantenmechanik - Übungen
So funktioniert es auch nicht richtig. - Je nach Parameter läuft es anders.
Re: Einführung in die Quantenmechanik - Übungen
Dann nimm die Lösung der DGLmit der Variablen x und dem Parameter z bzw. der Zeitabhängigkeit z(t)
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: Einführung in die Quantenmechanik - Übungen
Das ist ja das, was ich weiter oben schon geplottet habe, oder täusche ich mich?tomS hat geschrieben:Dann nimm die Lösung der DGLmit der Variablen x und dem Parameter z ...
Die Lösung der DGL ist doch
Natürlich kann ich den Plot auch für andere Wertebereiche und für komplexe z durchführen.
In den verlinkten Wikipedia-Artikeln kann ich die DGL nicht finden... vielleicht liege ich falsch.
Re: Einführung in die Quantenmechanik - Übungen
ja, deine Lösung der DGL ist korrekt; interessant wäre kein 2D PLot, sondern ein 1D Plot der Funktion für verschiedene t mit z(t) = exp(-it)
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: Einführung in die Quantenmechanik - Übungen
Du meinst, einfach z durch e^(-i t) ersetzen?

Also so etwas (Blau=Realteil; Rot=Imaginärteil):
Also so etwas (Blau=Realteil; Rot=Imaginärteil):
Re: Einführung in die Quantenmechanik - Übungen
Ja, super, wenn es das ist; ich denke, man bekommt einen ganz guten Eindruck davon, dass das Wellenpake eben kohärent bleibt und periodisch seine Form ändert.
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: Einführung in die Quantenmechanik - Übungen
Wenn die graphische Aufbereitung das ist, was Du meintest, dann sollte es stimmen.
Ich habe nur die Funktion

definiert.
Und das dann über eine Table geplottet:
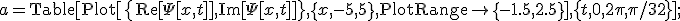
Und exportiert:
Export["a.gif", a]
Also, die X-Achse entspricht x, die Y-Achse dem Funktionswert und die Zeit eben t.
Ich habe nur die Funktion
definiert.
Und das dann über eine Table geplottet:
Und exportiert:
Export["a.gif", a]
Also, die X-Achse entspricht x, die Y-Achse dem Funktionswert und die Zeit eben t.
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: Einführung in die Quantenmechanik - Übungen
In den Operatoren sind nur x und p zeitabhängig, also sollte man einfachtomS hat geschrieben:Nun kann man aus diesen Bewegungsleichungen zunächst die für die Leiteroperatoren ableiten, in dem man die Definition derselben verwendet (Kapitel 3.3.1) und für diese dann die Zeitableitung gemäß 6.33 und 6.34 berechnet.
D.h. man erhält eine Bewegungsleichung mit da/dt. Berechne die doch mal.
und
schreiben, und die Ausdrücke für
und
Was dann?
Re: Einführung in die Quantenmechanik - Übungen
i omega ausklammern und scharf hinschauen ...
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Re: Einführung in die Quantenmechanik - Übungen
positronium hat geschrieben:Du meinst, einfach z durch e^(-i t) ersetzen?
Also so etwas (Blau=Realteil; Rot=Imaginärteil):
Hallo Leute,
entschuldigt wenn ich hier so reinplatze.
Mich hat der Plot -elektrisiert-.
Von Physik verstehe ich nichts, von Mathematik noch weniger, eigentlich garnichts.
Aber dieser Plot könnte das aussagen was ich unter "Spinschwingung" verstehe.
Nach meinen Vorstellungen führt jedes Teilchen, Elektron, Kernteilchen usw.
auch unser Universum, eine Art Schwingung aus.
Diese Schwingung erhält den Schwingkörper in seiner Einheit.
Diese Schwingung hat eine Vorzugsrichtung, darum lagern sich auch die beiden Elektronen auf -Orbital-1 immer so an dass sie sich nicht gegenseitig stören.
Die rote -Linie- symbolisiert den Schwingungzustand, die blaue die Wirkungsstärke die nach aussen geht.
Bin wieder weg.
Kurt
Wir werden erst begreifen wie genial die Natur ist wenn wir erkennen wie einfach sie funktioniert
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: Einführung in die Quantenmechanik - Übungen
Dann kommt für den ErzeugungsoperatortomS hat geschrieben:i omega ausklammern und scharf hinschauen ...
heraus.
Das i k x erinnert mich an den Exponenten in der e-Funktion, oder p könnte man durch
Re: Einführung in die Quantenmechanik - Übungen
k ist hier definiert mittels omega und m (lies im Skript nach); um es abzukürzen: rechts steht einfach wieder der Leiteroperator mal i omega
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
