Abenteuer-Universum

Ach so. Weil man die Summe als e^ schreiben kann, lässt man c[down]0[/down] ausserhalb des Bruchs.

So, und damit hat man eine erste Darstellung eines sogenannten kohärenten Zustandes als Eigenzustand des Vernichtungsoperators a:

$a|z\rangle = z|z\rangle$

$|z\rangle = e^{-|z|^2/2}\,\sum_{n=0}^\infty \frac{z^n}{\sqrt{n!}}|n\rangle$

Nun ist zu zeigen:

Es existiert eine geschlossene Darstellung als

$|z\rangle = A(z)|0\rangle$

d.h. der Operator A(z) ist zu konstruieren.

Das Skalarprodukt <z|w> für zwei komplexe Zahlen z und w ist zu betrachten.

Außerdem ist zu zeigen: die Zustände |z> erfüllen eine (geeignet verallgemeinerte) Vollständigkeitsrelation

tomS hat geschrieben: $|z\rangle = e^{-|z|^2/2}\,\sum_{n=0}^\infty \frac{z^n}{\sqrt{n!}}|z\rangle$

Muss das Ket am Ende nicht ein |n> sein?

Ich nehme mal an, dass statt z n in der Formel stehen sollte.

tomS hat geschrieben:Nun ist zu zeigen:

Es existiert eine geschlossene Darstellung als

$|z\rangle = A(z)|0\rangle$

d.h. der Operator A(z) ist zu konstruieren.

Weil der Operator auf |0> angewandt wird, sollte man auf der linken Seite n=0 setzen können.
$e^{-|z|^2/2}\frac{z^0}{\sqrt{0!}}|0\rangle=A(z)|0\rangle$
Es würde also auf der linken Seite die gesamte Summe heraus fallen.
$e^{-|z|^2/2}|0\rangle=A(z)|0\rangle$
Und |0> könnte man auch weg lassen, wodurch
$A(z)=e^{-|z|^2/2}$
wäre.
Ist das richtig?

Das kann nicht stimmen, da dein A(z) einfach eine Zahl ist, aber eine Zahl * |0> ist immer nur eine Zahl * |0>.

Ich sehe folgenden Lösungsansatz zur Konstruktion von A(z): durch 'hinschauen':

$A(z) = e^{f(z)a^\dagger} = \sum_{n=0}^\infty \frac{f^n(z)\,\left(a^\dagger\right)^n}{n!}$

Zu bestimmen ist die Funktion f(z)

Zu prüfen wäre dann, ob mit diesem Ansatz

$\langle n|A(z)|0\rangle = \langle n|z\rangle$

für das oben konstruierte |z> erfüllbar ist.

Du kannst auch rekursiv die Folge

$|0\rangle, a^\dagger |0\rangle, \left(a^\dagger\right)^2 |0\rangle, \ldots \left(a^\dagger\right)^n |0\rangle, \ldots$

betrachten

Das verstehe ich gar nicht.
Wie kommst Du auf den Ausdruck für A(z), und warum findet hier der adjungierte Vernichtungsoperator Anwendung?

Das ist einfach.

Die Darstellung des kohärenten Zustandes |z> sieht aus wie die Taylorreihe einer e-Funktion - mit Ausnahme der Wurzel im Nenner.

Die Reihe

$|0\rangle, a^\dagger |0\rangle, \left(a^\dagger\right)^2 |0\rangle, \ldots \left(a^\dagger\right)^n |0\rangle, \ldots$

generiert ebenfalls soetwas Ähnliches

$|0\rangle, a^\dagger |0\rangle = \sqrt{1!}|0\rangle, \left(a^\dagger\right)^2 |0\rangle = \sqrt{2!}|2\rangle, \ldots \left(a^\dagger\right)^n |0\rangle = \sqrt{(n+1)!}|n+1\rangle, \ldots$

jetzt mit einer Wurzel im Zähler.

Jetzt setze mal zunächst f(z) = z, entwickle A(z) als Taylorreihe und wende die Taylorreihe gliedweise auf |0> an.

$a^\dagger$ wirkt dabei as Erzeugungsoperator (natürlich ist das der adjungierte Vernichter)

tomS hat geschrieben:Jetzt setze mal zunächst f(z) = z, entwickle A(z) als Taylorreihe und wende die Taylorreihe gliedweise auf |0> an.

Ich versuche es - die Taylorreihe kannte ich noch nicht (also, mal abgesehen vom Namen

).
$A(z) = \sum_{n=0}^\infty \frac{f^n(z)\,\left(a^\dagger\right)^n}{n!}$
wird zu
$A(z) = \frac{z\,\left(a^\dagger\right)^0}{0!}+\frac{1\,\left(a^\dagger\right)^1}{1!}$
Danach sollte die Reihe abbrechen, weil die zweite Ableitung von f(z)=z, f''(z)=0 ist.
Es folgt:
$A(z) = z+a^\dagger$
und:
$A(z) = z|0\rangle+a^\dagger|0\rangle$

Daraus ergibt sich für
$\langle n|A(z)|0\rangle = \langle n|z\rangle$
$\langle n|\left(z|0\rangle+a^\dagger|0\rangle\right)|0\rangle = \langle n|z\rangle$
Aber auf der rechten Seite sehe ich jetzt ein Problem. Kann ich das
$|z\rangle = e^{-|z|^2/2}\,\sum_{n=0}^\infty \frac{z^n}{\sqrt{n!}}|n\rangle$
einfach einsetzen? - <n|z> ist ja ein Skalarprodukt... oder muss ich das erst irgendwie auflösen? Aber dann bleibt doch kein |z> mehr...

positronium hat geschrieben: $A(z) = \sum_{n=0}^\infty \frac{f^n(z)\,\left(a^\dagger\right)^n}{n!}$
wird zu
$A(z) = \frac{z\,\left(a^\dagger\right)^0}{0!}+\frac{1\,\left(a^\dagger\right)^1}{1!}$
Danach sollte die Reihe abbrechen, weil die zweite Ableitung von f(z)=z, f''(z)=0 ist.

Sorry, dass ich dich mit dem f(z) auf die falsche Spur gesetzt habe. Es geht um f(z) = z und um eine Taylorentwicklung von A(z), um z=0, nicht um eine Taylorentwicklung von f(z).

Zunächst mal die Taylorentwicklung der e-Funktion

$e^{za^\dagger} = \sum_{n=0}^\infty \frac{z^n (a^\dagger)^n}{n!}$

Dann die Wirkung des Erzeugungsoperators auf den Grundzustand |0>

$(a^\dagger)^n|0\rangle = \sqrt{n!}|n\rangle$

Also

$e^{za^\dagger}|0\rangle = \sum_{n=0}^\infty \frac{z^n (a^\dagger)^n}{n!}|0\rangle = \sum_{n=0}^\infty \frac{z^n }{n!}(a^\dagger)^n|0\rangle = \sum_{n=0}^\infty \frac{z^n }{n!}\sqrt{n!}|n\rangle = \sum_{n=0}^\infty \frac{z^n }{\sqrt{n!}}|n\rangle = e^{|z|^2/2}|z\rangle$

Daraus folgt

$e^{-|z|^2/2}\,e^{za^\dagger}|0\rangle = |z\rangle$

und damit findet man für A(z)

$A(z) = e^{-|z|^2/2+za^\dagger};\; A(z)|0\rangle = |z\rangle$

OK, Danke!
Also, wenn das so da steht, kann ich folgen, aber ich habe fast keine Ahnung davon, wie man auf die Gesamtrechnung bezogen auf die Rechenschritte kommt bzw. was sich dahinter verbirgt. - Was zu tun ist, hast ja eigentlich jedesmal Du geschrieben...

Dann sind die kohärenten Zustände (ich sammle mal, was gebraucht wird):
$|z\rangle = e^{-|z|^2/2}\,\sum_{n=0}^\infty \frac{z^n}{\sqrt{n!}}|n\rangle$
wird komplex konjugiert, und scheint vom Ausdruck her gleich zu bleiben, zu
$|z\rangle* = \langle z| = e^{-|z|^2/2}\,\sum_{n=0}^\infty \frac{z^n}{\sqrt{n!}}\langle n|$
und
$|w\rangle = e^{-|w|^2/2}\,\sum_{n=0}^\infty \frac{w^n}{\sqrt{n!}}|n\rangle$

Dann ergibt sich für das Skalarprodukt
$\langle z|w \rangle = e^{-|z|^2/2}\,e^{-|w|^2/2}\,\sum_{n=0}^\infty \frac{z^n}{\sqrt{n!}} \frac{w^n}{\sqrt{n!}} = e^{-|z|^2/2-|w|^2/2}\,\sum_{n=0}^\infty \frac{(z w)^n}{n!}$
$= e^{(-|z|^2-|w|^2)/2}\,e^{z w} = e^{(-|z|^2-|w|^2)/2 + z w}$

$|z\rangle = e^{-|z|^2/2}\,\sum_{n=0}^\infty \frac{z^n}{\sqrt{n!}}|n\rangle$
ist OK, aber es muss

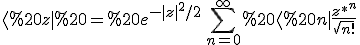
$\langle z| = e^{-|z|^2/2}\,\sum_{n=0}^\infty \langle n|\frac{{z^\ast}^n}{\sqrt{n!}}$

lauten.

Der Rest sieht bis auf diese Kleinigkeit gut aus.

Gut, dann muss es
$\langle z|w\rangle = e^{(-|z|^2-|w|^2)/2 + z* w}$
heissen.

Perfekt!

Jetzt etwas komplizierteres.

Die Eigenzustände |n> sind ja ein vollständiges Orthonormalsystem, d.h.

$P = \sum_n |n\rangle\langle n| = 1$

und

$\langle m|P|n\rangle = \delta_{mn}$

Für die Zusände |z> gilt die zweite Gleichung ja nicht, wie du selbst gezeigt hast; die |z> sind nicht orthogonal.

Aber man kann zeigen, dass sie vollständig sind, d.h. man konstruiert

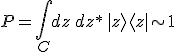
$P = \int_C dz\,dz^\ast\,|z\rangle\langle z| \sim 1$

und zeigt wiederum

$\langle m|P|n\rangle = \delta_{mn}$

Dabei musst du die Darstellung der |z> mittels der |n> verwenden und das Integral mittels Polarkoordinaten in der komplexen Ebene berechnen.

Das ist schwierig, aber ich probiere es.

Zuerst kopiere ich die beiden |z> und <z| hier noch einmal herein.

$|z\rangle = e^{-|z|^2/2}\,\sum_{n=0}^\infty \frac{z^n}{\sqrt{n!}}|n\rangle$
$\langle z| = e^{-|z|^2/2}\,\sum_{n=0}^\infty \langle n|\frac{{z^\ast}^n}{\sqrt{n!}}$
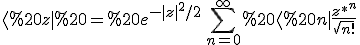
Dann erhält man für
$|z \rangle \langle z| = e^{-|z|^2/2}\,\sum_{n=0}^\infty \frac{z^n}{\sqrt{n!}}|n\rangle \,e^{-|z|^2/2}\,\sum_{n=0}^\infty \langle n|\frac{{z^\ast}^n}{\sqrt{n!}}$
$= e^{-|z|^2}\,\sum_{n=0}^\infty \frac{z^n}{\sqrt{n!}}|n\rangle \langle n|\frac{{z^\ast}^n}{\sqrt{n!}} = e^{-|z|^2}\,\sum_{n=0}^\infty \frac{z^n {z^\ast}^n}{n!}|n\rangle \langle n|$
Hier müsste man die Summe zerlegen können, in
$= e^{-|z|^2}\,\sum_{n=0}^\infty \frac{z^n {z^\ast}^n}{n!}\,\sum_{n=0}^\infty |n\rangle \langle n|$
worin die erste Summe in eine Exponentialfunktion umgewandelt, und die zweite Summe durch 1 ersetzt werden können sollte.
$= e^{-|z|^2}\,e^{z\,z\ast}\,1$
Daraus folgt
$|z \rangle \langle z|=e^{-|z|^2+z\,z\ast}$

Ehm... ich sehe gerade, dass damit |z><z| immer gleich 1 wäre. Also ist obiges falsch.

Liegt der Fehler beim Zerlegen der Summe? - Wahrscheinlich.

Du machst zwei Fehler.

Zum einen hast du zwei verschiedene Summen, d.h. auch zwei Summationsindizes m und n. Zum anderen bleiben Terme der Form |m><n| stehen, denn dafür gilt keine Orthogonalität. <m|n> entspricht dem Skalarprodukt zweier Vektoren und ergibt eine Zahl |m><n| entspricht einer Matrix. D.h.

$|z\rangle = \sum_m c_m(z)|m\rangle$

$\langle z|= \sum_n \langle n|c^\ast_n(z)$

$|z\rangle\langle z|= \sum_{m,n} c^\ast_n(z) c_m(z)|m\rangle\langle n|$

c[down]n[/down] steh dabei für den Koeffizienten vor |n> in |z>, also

$|z\rangle\langle z|= e^{-|z|^2} \sum_{m,n} \frac{{z^\ast}^n z^m}{\sqrt{m! n!}}|m\rangle\langle n|$

Jetzt kannst du |z><z| zwischen zwei weiteren Bra's und Ket's sandwichen

$\langle p|z\rangle\langle z|q\rangle= e^{-|z|^2} \sum_{m,n} \frac{{z^\ast}^n z^m}{\sqrt{m! n!}}\langle p|m\rangle\langle n|q\rangle = e^{-|z|^2} \sum_{m,n} \frac{{z^\ast}^n z^m}{\sqrt{m! n!}} \delta_{pm} \delta_{nq} = e^{-|z|^2} \frac{{z^\ast}^q z^p}{\sqrt{p! q!}}$

Jetzt das Integral in Polarkoordinaten ...

Ausgeschrieben und vereinfacht müsste dann
$|z\rangle\langle z|=e^{-z\,z\ast}\sum_{m,n}\frac{z^m\,z\ast^n}{\sqrt{m!}\,\sqrt{n!}}|m\rangle\langle n|$
heraus kommen.
Das mit dem Integrieren verstehe ich leider nicht. Natürlich kann ich so etwas konstruieren:
$\int_{0}^{2\pi}\int_{0}^{\infty} d\phi\,d r\,fuer\,z=r\cos(\phi)+i r \sin(\phi)...$
eingesetzt:
$\int_{0}^{2\pi}\int_{0}^{\infty} d\phi\,d r\,e^{-(r\cos(\phi)+i r \sin(\phi))\,(r\cos(\phi)-i r \sin(\phi))}\sum_{m,n}\frac{(r\cos(\phi)+i r \sin(\phi))^m\,(r\cos(\phi)-i r \sin(\phi))^n}{\sqrt{m!}\,\sqrt{n!}}|m\rangle\langle n|$
$=\int_{0}^{2\pi}\int_{0}^{\infty} d\phi\,d r\,e^{-r^2}\sum_{m,n}\frac{(e^{i\phi}r)^m(e^{-i\phi}r)^n}{\sqrt{m!}\,\sqrt{n!}}|m\rangle\langle n|$
Wahrscheinlich ist das falsch. Was kann ich damit machen? Oder wie muss ich das mit der Integration in der komplexen Ebene verstehen?

Gerade sehe ich, dass Du noch etwas hinzu gefügt hast - muss ich jetzt erst lesen.

Du bist so zeimlich auf der richtigen Spur.

Es geht um den Nachweis, dass der Operator P

$P = \int_C dz\,dz^\ast\,|z\rangle\langle z|$

proportional zum Eins-Operator also der "unendlich-dimensionalen Einheitsmatrix" ist. Dazu überlegen wir uns, dass dann

$\langle p|P|q\rangle \sim \delta_{pq}$

gelten muss.

D.h. du musst entweder wie von mir im letzten Post geschrieben das Matrixelement

$\langle p|z\rangle\langle z|q\rangle= e^{-|z|^2} \sum_{m,n} \frac{{z^\ast}^n z^m}{\sqrt{m! n!}}\langle p|m\rangle\langle n|q\rangle = e^{-|z|^2} \sum_{m,n} \frac{{z^\ast}^n z^m}{\sqrt{m! n!}} \delta_{pm} \delta_{nq} = e^{-|z|^2} \frac{{z^\ast}^q z^p}{\sqrt{p! q!}}$

berechnen, oder du schaffst es, die Auswertung des Integrals ohne dieses Matrixelement direkt auf den Operator anzuwenden; das wäre dein Weg, der zumindest nicht schlecht ausschaut. Dazu schreibst du deine letzte Formel wie folgt um (ich korrigiere einen kleinen Fehler: statt dr bekommst du dr r im Flächenelement)

$\int_C dz\,dz^\ast\,|z\rangle\langle z| = \int_{0}^{2\pi}\int_{0}^{\infty} d\phi\,d r\,r\,e^{-r^2}\sum_{m,n}\frac{(e^{i\phi}r)^m(e^{-i\phi}r)^n}{\sqrt{m!}\,\sqrt{n!}}|m\rangle\langle n| = \sum_{m,n} \frac{1}{\sqrt{m! n!}} |m\rangle\langle n| \int_{0}^{\infty} d r\,r\,r^m\,r^n\,e^{-r^2}\,\int_{0}^{2\pi} d\phi\,e^{im\phi}\,e^{-in\phi}$

Jetzt machst du eine Fallunterscheidung für m gleich n und für m ungleich n.

Für m gleich n, d.h. für die 'Hauptdiagonale' der Matrix, erwartest du, dass eine Eins rauskommt; für m ungleich n erwartest du eine Null; das liefert dir genau die Winkelintegration. Im Falle m gleich n liefert dir die r-Integration dann noch einen Normierungsfaktor, das ist sozusagen Fleißarbeit, das mit den Fakultäten richtig hinzubekommen; das r-Integral kann man explizit berechnen (ist eine ganz gute Übung und man lernt ein paar Tricks), kann man aber auch nachschauen.

Ich habe es versucht, aber was heraus kommt, muss falsch sein.
Für die Fallunterscheidung mit m=n habe ich o eingesetzt. Dadurch kann eine Summe wegfallen und es wird statt über m und n nur noch über o summiert. Alles ausgetauscht, und vereinfacht, erhalte ich:
$\sum_{o} \frac{1}{o!} |o\rangle\langle o|\,\frac{o!}{2}\,2\pi=\pi\sum_{o}|o\rangle\langle o|$

Zunächst mal m ungleich n:

Hier musst du dich nur davon überzeugen, dass

$\int_{0}^{2\pi} d\phi\,e^{im\phi}\,e^{-in\phi} = 0$

ist.

Dann für m gleich n:
- es wird nur noch über m=n summiert
- in jedem Term wird m=0n gesetzt
- im Winkelintegral steht Null im Exponenten, man erhält einfach 2π

Damit folgt

$2\pi \sum_n |n\rangle\langle n| \; \frac{1}{n!} \int_{0}^{\infty} dr\,r^{2n+1}\,e^{-r^2}$

Du musst nur noch zeigen, dass das Integral sich mit dem Term 1/n! weghebt

tomS hat geschrieben:Zunächst mal m ungleich n:

Hier musst du dich nur davon überzeugen, dass

$\int_{0}^{2\pi} d\phi\,e^{im\phi}\,e^{-in\phi} = 0$

ist.

Wenn man das Integral löst, erhält man:
$\frac{-i \left(e^{2 i (m-n) \pi }-1\right)}{m-n}$
Daraus folgt
$\frac{-i e^{2 i (m-n) \pi }}{m-n}+\frac{i}{m-n}=0$
und
$\frac{i}{m-n}=\frac{i e^{2 i (m-n) \pi }}{m-n}$
wodurch man schreiben kann
$i=i e^{2 i (m-n) \pi }$
$e^{2 i (m-n) \pi }=1$
Für ganzzahliges m-n folgt 1=1, also ist obige Aussage wahr.

tomS hat geschrieben: $2\pi \sum_n |n\rangle\langle n| \; \frac{1}{n!} \int_{0}^{\infty} dr\,r^{2n+1}\,e^{-r^2}$

Das Integral ergibt
$\frac{n!}{2}$
mit
$\frac{1}{n!}$
bleibt 1/2.
Dann fällt bei 2pi die 2 weg und es bleibt
$\pi\sum_{n}|n\rangle\langle n|$
Aber das ist wieder das, was ich oben schon als Ergebnis hatte. Hmm.

Oben hast du aber gesagt, dass es falsch sein muss, und jetzt?

Sorry, wenn ich dich irritiert habe und du alles doppelt gerechnet haben solltest. Du hast mit deiner Rechnung völlig recht! Du hast gezeigt, dass die 'kontiuierlichen' kohärenten Zustände |z> ein verallgemeinertes, überabzählbares, vollständiges, normiertes (jedoch nicht orthogonales) System bilden. D.h. man kann auf diesem Hilbertraum die Zustände sowohl mittels der Eigenzustände |n> von H als auch mittels der Eigenzustände |z> von a beschreiben.

Ein letztes noch: die kohärenten Zustände spielen eine Rolle in der Quantenoptik sowie in der semiklassischen Analyse verschiedener Systeme. Sie haben die Eigenschaft, Zustände minimaler Unschärfe zu sein, d.h. sie minimieren Δx*Δp. Letzteres müsstest du explizit ausrechnen können, in dem du die Definition von Δ²x aus Gl. (2.66) sowie Δ²p aus (2.67) verwendest. Dann müsstest du Δx sowie Δp durch die Erzeuger und Vernichter ausdrücken und zwischen den Zuständen sandwichen. Das kannst du einmal für <n|Δ²x|n> * <n|Δ²p|n> und einmal für <z|Δ²x|z> * <z|Δ²p|z> tun. Danach würde ich die Übingen zum Formalismus beenden, ggf. noch Fragen zur Bedeutung diskutieren und wieder im Skript fortfahren.

tomS hat geschrieben:Oben hast du aber gesagt, dass es falsch sein muss, und jetzt?

Naja, dass im Ergebnis ein pi steht, finde ich immer noch etwas befremdlich.

tomS hat geschrieben:Sorry, wenn ich dich irritiert habe und du alles doppelt gerechnet haben solltest.

War schon richtig so; dann bleibt's besser im Gedächtnis.

Abenteuer-Universum

Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen