Hinweis auf die DSGVO: Auf unserer Seite werden keine Dritt-Anbieter-Cookies verwendet und nur Daten erfasst, welche für das Minimum an Board-Funktionalität notwendig sind.
Bevor Sie sich registrieren oder das Board verwenden, lesen Sie bitte zusätzlich die DSGVO-Erklärung, welche in der Navigationsleiste verlinkt ist.
Kurzfassung der unserer Meinung nach wichtigsten DSGVO-Punkte:
Es kann vorkommen, dass Benutzer eigenverantwortlich Videos oder sonstige Medien in ihren Beiträgen verlinken, welche beim Aufruf der Forenseite als Teil der Seite samt zugehörigem Material mitgeladen werden. Sollten Sie dies nicht wünschen, verwenden Sie beim Benutzen des Forums einen Blocker wie z.B. uMatrix, welcher das Laden von Inhaltsblöcken von Fremd-URLs effektiv unterbinden kann.
Wir blenden keine Werbung ein und schränken die Inhalte in keinster Weise bei Benutzung von Addblockern ein. Dadurch ist die Grundfunktionalität des Forums auch bei vollständigem Blockieren von Drittanbieter-Inhalten stets gegeben.
Cookies werden unsererseits nur verwendet um das Einloggen des Benutzers für die Dauer der Forenbenutzung zu speichern. Es steht dem Benutzer frei die Option 'Angemeldet bleiben' zu verwenden, damit der Cookie dauerhaft gespeichert bleibt und beim nächsten Besuch kein erneutes Einloggen mehr notwendig ist.
EMail-Adressen werden für Kontakt bei wichtigen Mitteilungen und zur Widerherstellung des Passwortes verwendet. Die verwendeten IPs können von uns ohne externe Hilfsmittel mit keiner realen Person in Verbindung gebracht werden und werden nach spätestens 7 Tagen gelöscht. Diese IPs werden höchstens verwendet um Neuanmeldungen unerwünschter oder gesperrter Nutzer zu identfizieren und zu unterbinden. Wir behalten uns daher vor bei Verdacht, die Frist für die IP-Löschung auf maximal 14 Tage zu verlängern.
Unsere Webseite läuft auf einem virtuellen Linux-Server, welcher von einem externen Anbieter gehostet wird. Etwaige Verstöße der DSGVO-Auflagen seitens dieses deutschen Hosters können wir nicht feststellen und somit auch nicht verfolgen.
Wir halten Backups unserer Datenbanken, welche in regelmäßigen Abständen als Schutz vor Katastrophen, Hackerangriffen und sonstigen Ausfällen erstellt werden. Sollte ein Nutzer die Löschung seiner Daten wünschen, betrachten wir es als Unzumutbar die Backups auch von den Daten zu befreien, da es sich hierbei um eine mehrtägiges Unterfangen handelt - dies ist für eine Einzelperson beim Betrieb eines privaten Forums nicht zumutbar möglich ohne das Backup komplett zu löschen.
Sollten Sie etwas gegen die dauerhafte anonyme Speicherung ihrer EMail-Adresse, ihres Pseudonyms und ihrer Beiträge in einem Backup haben, sehen Sie von der Registrierung in diesem Forum ab. Für Mitglieder, welche vor dem 25.05.2018 registriert waren steht jedoch das Recht im Raum, eine Löschung der Datenbank-Backups zu beantragen.
Wenn dies Ihr erster Besuch hier ist, lesen Sie bitte zunächst die FAQs sowie die wesentlichen Regeln zur Benutzung des Forums.
Um an den Diskussionen teilnehmen zu können, müssen Sie sich zunächst registrieren.
Bevor Sie sich registrieren oder das Board verwenden, lesen Sie bitte zusätzlich die DSGVO-Erklärung, welche in der Navigationsleiste verlinkt ist.
Kurzfassung der unserer Meinung nach wichtigsten DSGVO-Punkte:
Es kann vorkommen, dass Benutzer eigenverantwortlich Videos oder sonstige Medien in ihren Beiträgen verlinken, welche beim Aufruf der Forenseite als Teil der Seite samt zugehörigem Material mitgeladen werden. Sollten Sie dies nicht wünschen, verwenden Sie beim Benutzen des Forums einen Blocker wie z.B. uMatrix, welcher das Laden von Inhaltsblöcken von Fremd-URLs effektiv unterbinden kann.
Wir blenden keine Werbung ein und schränken die Inhalte in keinster Weise bei Benutzung von Addblockern ein. Dadurch ist die Grundfunktionalität des Forums auch bei vollständigem Blockieren von Drittanbieter-Inhalten stets gegeben.
Cookies werden unsererseits nur verwendet um das Einloggen des Benutzers für die Dauer der Forenbenutzung zu speichern. Es steht dem Benutzer frei die Option 'Angemeldet bleiben' zu verwenden, damit der Cookie dauerhaft gespeichert bleibt und beim nächsten Besuch kein erneutes Einloggen mehr notwendig ist.
EMail-Adressen werden für Kontakt bei wichtigen Mitteilungen und zur Widerherstellung des Passwortes verwendet. Die verwendeten IPs können von uns ohne externe Hilfsmittel mit keiner realen Person in Verbindung gebracht werden und werden nach spätestens 7 Tagen gelöscht. Diese IPs werden höchstens verwendet um Neuanmeldungen unerwünschter oder gesperrter Nutzer zu identfizieren und zu unterbinden. Wir behalten uns daher vor bei Verdacht, die Frist für die IP-Löschung auf maximal 14 Tage zu verlängern.
Unsere Webseite läuft auf einem virtuellen Linux-Server, welcher von einem externen Anbieter gehostet wird. Etwaige Verstöße der DSGVO-Auflagen seitens dieses deutschen Hosters können wir nicht feststellen und somit auch nicht verfolgen.
Wir halten Backups unserer Datenbanken, welche in regelmäßigen Abständen als Schutz vor Katastrophen, Hackerangriffen und sonstigen Ausfällen erstellt werden. Sollte ein Nutzer die Löschung seiner Daten wünschen, betrachten wir es als Unzumutbar die Backups auch von den Daten zu befreien, da es sich hierbei um eine mehrtägiges Unterfangen handelt - dies ist für eine Einzelperson beim Betrieb eines privaten Forums nicht zumutbar möglich ohne das Backup komplett zu löschen.
Sollten Sie etwas gegen die dauerhafte anonyme Speicherung ihrer EMail-Adresse, ihres Pseudonyms und ihrer Beiträge in einem Backup haben, sehen Sie von der Registrierung in diesem Forum ab. Für Mitglieder, welche vor dem 25.05.2018 registriert waren steht jedoch das Recht im Raum, eine Löschung der Datenbank-Backups zu beantragen.
Wenn dies Ihr erster Besuch hier ist, lesen Sie bitte zunächst die FAQs sowie die wesentlichen Regeln zur Benutzung des Forums.
Um an den Diskussionen teilnehmen zu können, müssen Sie sich zunächst registrieren.
Einführung in die Quantenmechanik - Übungen
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: Einführung in die Quantenmechanik
Vielen Dank Euch beiden!
Dann könnten wir von meiner Seite aus gerne weiter machen, aber ich merke, dass ich von Seite zu Seite mangels Übung unsicherer werde. Gibt es denn an dem Punkt schon sinnvolles, das ich mal durchzurechnen versuchen könnte?
Dann könnten wir von meiner Seite aus gerne weiter machen, aber ich merke, dass ich von Seite zu Seite mangels Übung unsicherer werde. Gibt es denn an dem Punkt schon sinnvolles, das ich mal durchzurechnen versuchen könnte?
Re: Einführung in die Quantenmechanik
Da müsstest du mal nach QM Übungen & Lösungen googeln.
Oder eine interessante Aufgabe: versuche doch mal, Eigenzustände der Vernichtungsoperatoren beim harmonischen Oszillator zu konstruieren
Oder eine interessante Aufgabe: versuche doch mal, Eigenzustände der Vernichtungsoperatoren beim harmonischen Oszillator zu konstruieren
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Einführung in die Quantenmechanik - Übungen
Hier bin ich mir nicht sicher, ob ich das verstehe. Dazu müsste ich doch wegen der Ortsabhängigkeit des Potentials von der allgemeinen Darstellung in die Ortsdarstellung wechseln. Aber dann liefe das doch fast auf das hinaus, was in Kapitel 3.3.1 berechnet wurde.tomS hat geschrieben:Oder eine interessante Aufgabe: versuche doch mal, Eigenzustände der Vernichtungsoperatoren beim harmonischen Oszillator zu konstruieren
Also, der Vernichtungsoperator ist
Dann würde die allgemeine Darstellung
zu
Wie oben gesagt, wäre das doch praktisch gleich dem Kapitel 3.3.1. Man bekäme für jeden Eigenwert von
Oder bin ich jetzt völlig daneben?
Re: Einführung in die Quantenmechanik
Eigenwerte zu a sin etwas anderes als Eigenwerte zu H. Insbs. ist ja zunächst a|n>

und somit ist das zunächst kein Eigenvektor.
Hinweis: a ist nicht hermitwch, daher muss der Eigenwert nicht reell sein; suche also Lösungen der Gleichung
|z\rangle = 0)
mit komplexem (!) z.
Noch ein Hinweis: du benötigst die Ortsdarstellung nicht
und somit ist das zunächst kein Eigenvektor.
Hinweis: a ist nicht hermitwch, daher muss der Eigenwert nicht reell sein; suche also Lösungen der Gleichung
mit komplexem (!) z.
Noch ein Hinweis: du benötigst die Ortsdarstellung nicht
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: Einführung in die Quantenmechanik - Übungen
Jetzt verstehe ich kein Wort mehr, und bin total kaputt. Ich kann mich an nichts in dem Skript erinnern, was hier weiter helfen könnte.
Wie entsteht die Formel|z\rangle = 0) ? (In Wikipedia hat die Formel zur Eigenwertberechnung eine andere Form.) Darin ist doch a der Vernichtungsoperator, wie ich ihn oben als V bezeichnet habe; dadurch hat man aber doch schon wieder die Ortsabhängigkeit. Und wie kann z als komplexe Zahl in dem Ket stehen? Insgesamt würde also irgend eine gefährliche DGL entstehen - aber wahrscheinlich ist das eh falsch, was ich mir hier von der Seele schreibe.
? (In Wikipedia hat die Formel zur Eigenwertberechnung eine andere Form.) Darin ist doch a der Vernichtungsoperator, wie ich ihn oben als V bezeichnet habe; dadurch hat man aber doch schon wieder die Ortsabhängigkeit. Und wie kann z als komplexe Zahl in dem Ket stehen? Insgesamt würde also irgend eine gefährliche DGL entstehen - aber wahrscheinlich ist das eh falsch, was ich mir hier von der Seele schreibe.
Wie entsteht die Formel
Re: Einführung in die Quantenmechanik - Übungen
Zunächst mal ist das eine gan z normale Eigenwertgleichung "Operator minus Eigenwert angewandt auf Eigenzustand ist Null".
z sei eine beliebige komplexe Zahl; gesicht sind alle z's die als Eigenwerte auftreten können sowie die zugehörigen Eigenzustände |z>. Der Ansatz lautet

Jetzt musst du die Koeffizienten c[down]n[/down] bestimmen.
z sei eine beliebige komplexe Zahl; gesicht sind alle z's die als Eigenwerte auftreten können sowie die zugehörigen Eigenzustände |z>. Der Ansatz lautet
Jetzt musst du die Koeffizienten c[down]n[/down] bestimmen.
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: Einführung in die Quantenmechanik - Übungen
Gut, also die Gleichung |z\rangle = 0) ist mir jetzt glaube ich klar. Das
ist mir jetzt glaube ich klar. Das  dürfte die Entwicklung der Eigenzustände nach den Basisvektoren des Hilbert-Raums sein.
dürfte die Entwicklung der Eigenzustände nach den Basisvektoren des Hilbert-Raums sein.
Aber mehr verstehe ich nicht.
Jetzt könnte ich zwar die zweite Gleichung in die erste einsetzen
 \sum_{n=0}^\infty c_n\,|n\rangle= 0)
wodurch die abstrakte Darstellung von |z> auf die Basisvektoren abgebildet würde, aber dann müsste ich doch den Vernichtungsoperator auch noch einsetzen, und es käme
-z) \sum_{n=0}^\infty c_n\,|n\rangle= 0)
heraus.
Falls das überhaupt etwas sinnvolles ist, kann ich das unmöglich lösen.
Ich habe schon versucht, eine Musterrechnung dazu zu finden, lande aber immer nur bei der Aufgabe zum harmonischen Oszillator.
Aber mehr verstehe ich nicht.
Jetzt könnte ich zwar die zweite Gleichung in die erste einsetzen
wodurch die abstrakte Darstellung von |z> auf die Basisvektoren abgebildet würde, aber dann müsste ich doch den Vernichtungsoperator auch noch einsetzen, und es käme
heraus.
Falls das überhaupt etwas sinnvolles ist, kann ich das unmöglich lösen.
Ich habe schon versucht, eine Musterrechnung dazu zu finden, lande aber immer nur bei der Aufgabe zum harmonischen Oszillator.
Re: Einführung in die Quantenmechanik - Übungen
Du musst keineswegs die Darstellung des Vernichtungsoperators mittels x und p einsetzen; alles was du brauchst ist

Daraus kannst du eine Rekursionsbedingung für die c's ableiten.
Daraus kannst du eine Rekursionsbedingung für die c's ableiten.
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: Einführung in die Quantenmechanik - Übungen
Das von oben
\sum _{n=0}^{\infty } c_n|n\rangle =0)
könnte ich ausmultiplizieren zu
=0)
und

einsetzen, sodass
=0)
entsteht, und daraus kann man eine Rekursionsformel machen:
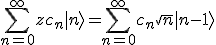
Meintest Du das?
Ich sehe, dass mir noch ein grundlegendes Verständnis fehlt.
könnte ich ausmultiplizieren zu
und
einsetzen, sodass
entsteht, und daraus kann man eine Rekursionsformel machen:
Meintest Du das?
Ich sehe, dass mir noch ein grundlegendes Verständnis fehlt.
Re: Einführung in die Quantenmechanik - Übungen
ja, so in etwa; jetzt multipliziere mal von links mit einem bra <m|
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: Einführung in die Quantenmechanik - Übungen
Dann entsteht
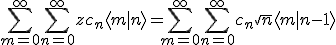
worin die Skalarprodukte nur 1 ergeben, wenn links m=n bzw. rechts m=n-1 ist, so dass die Bras und Kets wegfallen, und man schreiben kann:

Aber wenn das richtig ist, hat man hier eine unendliche divergierende Reihe, mit der ich nichts anzufangen weiss, obwohl irgendwie ein Startwert und die Veränderung je 1 m ermittelt werden können sollte.
worin die Skalarprodukte nur 1 ergeben, wenn links m=n bzw. rechts m=n-1 ist, so dass die Bras und Kets wegfallen, und man schreiben kann:
Aber wenn das richtig ist, hat man hier eine unendliche divergierende Reihe, mit der ich nichts anzufangen weiss, obwohl irgendwie ein Startwert und die Veränderung je 1 m ermittelt werden können sollte.
Re: Einführung in die Quantenmechanik - Übungen
Wir starten mit deiner obigen Gleichung
=0)
Jetzt nur multiplizieren mit <m|, d.h. projizieren auf den m-ten Zustand
=0)
=0)
Und jetzt fällt die Summe weg ...
Jetzt nur multiplizieren mit <m|, d.h. projizieren auf den m-ten Zustand
Und jetzt fällt die Summe weg ...
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: Einführung in die Quantenmechanik - Übungen
Aber deswegen entfällt doch nicht der Zwang zum Summieren, oder? - Würde man m und n als Variablen auffassen, wäre dann die Gleichung nicht unbrauchbar? Also, wenn ich mir m und n als Indizes einer Matrix vorstelle, wäre der zweite Term in der Diagonalen ungleich 0 und der erste eine Zeile darüber. Bei m=n müsste z oder  gleich 0 sein, und bei m=n-1 müsste
gleich 0 sein, und bei m=n-1 müsste  immer gleich 0 sein.
immer gleich 0 sein.
Re: Einführung in die Quantenmechanik - Übungen
Natürlich entfällt nicht der Zwang zum ssummieren,aber es bleibt nur noch jeweils ein Term übrig; es gilt
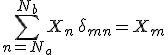
wenn m im Summationsbereich liegt (ansonsten Null)
wenn m im Summationsbereich liegt (ansonsten Null)
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Re: Einführung in die Quantenmechanik - Übungen
Ich komme nochmal auf die letzte Gleichung zurück:
=0)
Zunächst m=0:
Im ersten Term gilt mit m=0 auch n-1 = 0, also n=1
Im zweiten Term gilt mit m=0 dann n=0
Also

Daraus bekommst ermittelst du c[down]1[/down] als c[down]1[/down](c[down]0[/down]); für alle weiteren m = 1, 2, ... ergibt sich dann rekursiv die Folge der c[down]2[/down], c[down]3[/down], ...; diese ist bestimmt bis auf eine multiplikative Konstante, also letztlich den Startwert c[down]0[/down], der durch Normierung <z|z> = 1 festgelet wird.
Zunächst m=0:
Im ersten Term gilt mit m=0 auch n-1 = 0, also n=1
Im zweiten Term gilt mit m=0 dann n=0
Also
Daraus bekommst ermittelst du c[down]1[/down] als c[down]1[/down](c[down]0[/down]); für alle weiteren m = 1, 2, ... ergibt sich dann rekursiv die Folge der c[down]2[/down], c[down]3[/down], ...; diese ist bestimmt bis auf eine multiplikative Konstante, also letztlich den Startwert c[down]0[/down], der durch Normierung <z|z> = 1 festgelet wird.
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: Einführung in die Quantenmechanik - Übungen
Gestern war ich recht beschäftigt; deshalb konnte ich mich leider nicht darauf konzentrieren.
Nach Deinem letzten Posting ist mir das mit der Summe klarer. Man wählt also ein bestimmtes m, zweckmässigerweise m=0, wodurch man wegen weiss, welche Werte für n sinnvoll sind.
weiss, welche Werte für n sinnvoll sind.
Die Aufgabe hätte ich alleine nie lösen können.
Vielen Dank für Deine Mühe!
Nach Deinem letzten Posting ist mir das mit der Summe klarer. Man wählt also ein bestimmtes m, zweckmässigerweise m=0, wodurch man wegen
Die Aufgabe hätte ich alleine nie lösen können.
Vielen Dank für Deine Mühe!
Re: Einführung in die Quantenmechanik - Übungen
Die Aufgabe ist noch nicht beendet.
- du sollst explizit die Koeffizienten c[down]n[/down] bestimmen, c[down]0[/down] mittels Normierung <z|z> = 1
- dann eine gesxchlossene Form als |z> = A(z)|0>
- sowie die Vollständigkeit der Zustände |z>
- ...
;-)
- du sollst explizit die Koeffizienten c[down]n[/down] bestimmen, c[down]0[/down] mittels Normierung <z|z> = 1
- dann eine gesxchlossene Form als |z> = A(z)|0>
- sowie die Vollständigkeit der Zustände |z>
- ...
;-)
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: Einführung in die Quantenmechanik - Übungen
Oh...tomS hat geschrieben:Die Aufgabe ist noch nicht beendet.
Ich dachte, die Definition der Reihe für c[down]n[/down] wäre gesucht.
Ich weiss nicht, was ich mit <z|z>=1 machen kann, um einen Zahlenwert zu bekommen. Nur das Skalarprodukt könnte man in der Form schreibentomS hat geschrieben:- du sollst explizit die Koeffizienten c[down]n[/down] bestimmen, c[down]0[/down] mittels Normierung <z|z> = 1
dann muss wohl die Summe eliminiert werden. Aber: keine Ahnung!
Bist Du Dir sicher, dass ich das mit dem Inhalt aus den Kapiteln 5.1 bis 5.3 lösen können müsste?
Re: Einführung in die Quantenmechanik - Übungen
a) Zunächst benötigst du die Rekursionsformel für die c[down]n[/down] sowie die explizite Darstellung für c[down]n[/down].
b) Anschließend berechnest du

und setzt dies gleich Eins; daraus folgt der Koeffizient c[down]0[/down]
b) Anschließend berechnest du
und setzt dies gleich Eins; daraus folgt der Koeffizient c[down]0[/down]
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: Einführung in die Quantenmechanik - Übungen
Die Rekursionsformel lautettomS hat geschrieben:a) Zunächst benötigst du die Rekursionsformel für die c[down]n[/down] sowie die explizite Darstellung für c[down]n[/down].
und deshalb ist
Wenn ich das in das von Dir berechnete
einsetze, folgt
Weil c[down]0[/down] gesucht ist, setze ich n=1, wodurch die Summe wegfallen kann, und setze gleich 1
Daraus folgt
Das hiesse dann, dass
und
...sieht irgendwie seltsam aus.
Re: Einführung in die Quantenmechanik - Übungen
nein, gar nicht seltsam, unter der Wurzel steht einfach ein n! (n Fakultät)
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: Einführung in die Quantenmechanik - Übungen
Dann schreibt man also einfach?
=\frac{z^{n-1}}{\sqrt{n!}})
Re: Einführung in die Quantenmechanik - Übungen
Aus dem Gedächtnis:
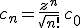
und damit jetzt <z|z>
und damit jetzt <z|z>
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
-
positronium
- Ehrenmitglied

- Beiträge: 2832
- Registriert: 2. Feb 2011, 20:13
Re: Einführung in die Quantenmechanik - Übungen
Also, intomS hat geschrieben:und damit jetzt <z|z>
einsetzen, und vereinfachen zu
Für c[down]0[/down] könnte man doch, damit es schöner aussieht, 1/z einsetzen, so dass
entsteht, oder braucht man c[down]0[/down] an anderer Stelle für einen anderen Startwert als Variable?
Muss ich jetzt von <z|z> auf |z> kommen?
Re: Einführung in die Quantenmechanik - Übungen
Leichte Korrektur bzgl. der Beträge:

Daraus folgt für c[down]0[/down]
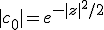
Daraus folgt für c[down]0[/down]
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper