Seite 1 von 1
Stimmt meine Intuition zur Stetigkeit?
Verfasst: 30. Dez 2015, 22:55
von Pippen
Ein Funktion ist stetig, wenn es im Rahmen des Definitionsbereiches keine Zahl x gibt, für die f(x) nichts (auch nicht 0) ausspuckt. Stetige Funktionen müssen IR als Definitions- und Wertebereich haben. Stetigkeit = Kontinuität.
Re: Stimmt meine Intuition zur Stetigkeit?
Verfasst: 31. Dez 2015, 00:00
von tomS
Nee.
Stetigkeit bedeutet, dass f(x) keine Spungstelle hat; d.h. dass wenn |x - y| gegen Null geht, auch |f(x) - f(y)| gegen Null gehen muss.
Re: Stimmt meine Intuition zur Stetigkeit?
Verfasst: 31. Dez 2015, 01:34
von Alberich
Da schreibt mein alter Lehrer (L.Vietoris 1951):
Die in einer Umgebung von a definierte Funktion f(x) heißt an der Stelle a stetig, wenn
lim f(x) =f(a) ist wenn x-->a+ und x-->a-.
Cauchy von links bzw. rechts.
MfG
Alberich
 http://www.mathe-online.at/mathint/stet/i.html
http://www.mathe-online.at/mathint/stet/i.html
Re: Stimmt meine Intuition zur Stetigkeit?
Verfasst: 31. Dez 2015, 09:37
von Skeltek
Deine Intuition stimmt nicht ganz.
Die Funktion selbst ist stetig, wenn sie in jedem Punkt ihrest Definitionsbereiches stetig ist.
Ob die Punkte selbst stetig sind würde ich mich daran orientieren, was Alberich und tomS gesagt haben.
Allerdings gibt es auch Ausnahmefälle wenn man es so grob formuliert.
Versuche am besten herauszufinden, welche der äquivalenten Definitionen dein Lehrer oder Professor benutzt (welche bildliche Vorstellung du davon entwickelst und festigst ist wichtig, da ein späteres gedankliches umformulieren unter Zeitdruck große Schwierigkeiten machen kann).
Übernimmt die Definition für welche eure Prüfungsaufgaben dann ausgelegt werden.
Zu Ausnahmen:
Man kann sich zum Beispiel eine Funktion vorstellen, welche umso mehr unstetigkeitsstellen hat, je näher man an den Punkt x
0 heran kommt. Im Punkt x
0 ist sie stetig und differenzierbar, aber nicht in seiner Umgebung differenzierbar oder stetig.
Ich male dir mal ein Bild wenn ich Zeit habe

ps: Hier das versprochene Bild
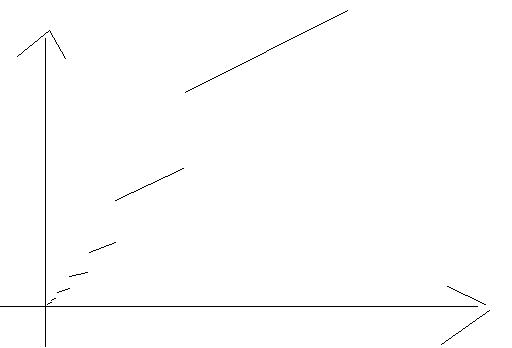
- Stetig nur in einem Punkt.jpg (7.69 KiB) 10434 mal betrachtet
Die Funktion erfüllt obige Stetigkeitsdefinitionen im Punkt x
0=0.
(Falls ich mich da jetzt nicht grob verdacht habe)
Trotzdem kann man nur den "Punkt" x
0=0 zeichnen ohne den stift abzusetzen aber nicht seine Umgebung.
Re: Stimmt meine Intuition zur Stetigkeit?
Verfasst: 31. Dez 2015, 15:11
von tomS
Um zu untersuchen, ob die Funktion in x = 0 stetig ist, müsstest du die exakte Definition angeben. Dass sie da differenzierbaren ist bezweifle ich (aber auch dazu benötigt man eine exakte Definition)
Re: Stimmt meine Intuition zur Stetigkeit?
Verfasst: 31. Dez 2015, 17:42
von Skeltek
@tomS:
Ja, du hast Recht mit der Differenzierbarkeit.
Allerdings ist Differenzierbarkeit keine Voraussetzung für Stetigkeit, wie man leicht an der impliziten Darstellung der Funktion mit x=y^3 sehen kann (diese hat bei x=0 als Ableitung unendlich).
War etwas faul bei dem Bild und hatte keinen Nerv eine Vorschrift anzugeben, aber ich hoffe es kommt rüber was ich sagen wollte.
Die Funktion hat bei den Strichen überall die Steigung 1/2, die Strichlänge halbiert sich bei jedem Strich näher an der y-Achse, die rechten oberen Enden der Striche liegen auf der Winkelhalbierenden.
Soweit ich das beurteilen kann, erüllt die Funktion im Punkt x=0 die Stetigkeitsvoraussetzungen; falls ich mich grob vertan haben sollte bitte melden ^^
Re: Stimmt meine Intuition zur Stetigkeit?
Verfasst: 31. Dez 2015, 18:57
von tomS
Skeltek hat geschrieben:Allerdings ist Differenzierbarkeit keine Voraussetzung für Stetigkeit
Stimmt.
Skeltek hat geschrieben:... aber ich hoffe es kommt rüber was ich sagen wollte.
Ja.
Re: Stimmt meine Intuition zur Stetigkeit?
Verfasst: 1. Jan 2016, 14:22
von Pippen
tomS hat geschrieben:Nee.
Stetigkeit bedeutet, dass f(x) keine Spungstelle hat; d.h. dass wenn |x - y| gegen Null geht, auch |f(x) - f(y)| gegen Null gehen muss.
Naja, was bedeutet das anderes als folgendes:
Stetigkeit: egal was für eine reelle Zahl man in eine Funktionsvorschrift einsetzt, es kommt ein Ergebnis raus. Dagegen ist eine Funktion nicht-stetig, wenn es mindestens eine reelle Zahl gibt, für welche kein Funktionswert existiert.
Bsp.: x² ist stetig, denn egal welche reelle Zahl ich in x eingebe, es gibt ein reelles Ergebnis; 1/x ist nicht stetig, denn für x=0 gibt es kein Ergebnis.
Wenn meine intuitive Definition falsch wäre, dann müsste es mind. ein Gegenbsp. geben....
Re: Stimmt meine Intuition zur Stetigkeit?
Verfasst: 2. Jan 2016, 00:14
von Skeltek
1/x ist auf dem gesammten Definitionsbereich R\{0} in jedem Punkt stetig.
1/x ist nur unstetig auf R, wenn man den Definitionsbereich durch y(0):=a erweitert.
->Stetigkeit ist die Eigenschaft eines Punktes und dem "Übergang" zu seiner unmittelbaren infinitesimalen Umgebung.
Stetigkeit ist keine Eigenschaft einer Funktion oder Kurve.
Es ist eine (umgangs)sprachliche Vereinfachung zusagen, dass eine "Funktion stetig ist":
Was man damit meint ist, dass sie in jedem ihrer Punkte stetig ist.
->Umgangssprachlich nur für das Verständniss bzw Vorstellungsbildung:
Eine Funktion ist nicht stetig in einem Punkt, wenn sie links oder rechts von diesem Punkt in einem infinitesimalen Abstand einen "Sprung" macht, der größer 0 ist.
Gruß, Skel
ps: Deshalb ist auch 1/x stetig, weil keiner der Punkte im Definitionsbereich einen Sprung in seiner "infinitesimalen Umgebung" aufweisen kann.
Egal wie nahe man an 0 geht, findet man dort mit einem Vergrößerungsglas keinen Sprung vor.
Re: Stimmt meine Intuition zur Stetigkeit?
Verfasst: 2. Jan 2016, 00:25
von tomS
Pippen hat geschrieben:tomS hat geschrieben:Nee.
Stetigkeit bedeutet, dass f(x) keine Spungstelle hat; d.h. dass wenn |x - y| gegen Null geht, auch |f(x) - f(y)| gegen Null gehen muss.
Naja, was bedeutet das anderes als folgendes:
Stetigkeit: egal was für eine reelle Zahl man in eine Funktionsvorschrift einsetzt, es kommt ein Ergebnis raus. Dagegen ist eine Funktion nicht-stetig, wenn es mindestens eine reelle Zahl gibt, für welche kein Funktionswert existiert.
Das bedeutet durchaus etwas anderes.
Betrachte die Funktion
f(x) = 0 für x < 0
f(x) = 1 für x ≥ 0
Die Funktion hat für jedes x einen eindeutigen Funktionswert, ist jedoch bei x = 0 unstetig, da hier ein Sprung von 0 auf 1 vorliegt.
Re: Stimmt meine Intuition zur Stetigkeit?
Verfasst: 2. Jan 2016, 14:31
von Skeltek
Oder anders ausgedrückt
limn->unendlich (x-n)
^.^
Re: Stimmt meine Intuition zur Stetigkeit?
Verfasst: 4. Jan 2016, 09:00
von tomS
Skeltek hat geschrieben:Oder anders ausgedrückt
limn->unendlich (x-n)
^.^
Nee, falsch
Re: Stimmt meine Intuition zur Stetigkeit?
Verfasst: 4. Jan 2016, 13:38
von Skeltek
Hab die Vorzeichen falsch gelesen ^^
Re: Stimmt meine Intuition zur Stetigkeit?
Verfasst: 5. Jan 2016, 01:16
von Pippen
tomS hat geschrieben:
Betrachte die Funktion
f(x) = 0 für x < 0
f(x) = 1 für x ≥ 0
Die Funktion hat für jedes x einen eindeutigen Funktionswert, ist jedoch bei x = 0 unstetig, da hier ein Sprung von 0 auf 1 vorliegt.
Verstehe ich das richtig: Jede Funktion der Art 1. f(x) = a für x < b & 2. f(x) = a+1 für x ≥ b (x, a, b € IR) wäre danach unstetig?
Re: Stimmt meine Intuition zur Stetigkeit?
Verfasst: 5. Jan 2016, 08:14
von tomS
Ja.
Oder allgemeiner zu Idee "Eine Funktion ist stetig, wenn der Graph der Funktion ohne Absetzen des Stiftes gezeichnet werden kann ... Eine Funktion f heißt stetig, wenn hinreichend kleine Änderungen des Argumentes x zu beliebig kleinen Änderungen des Funktionswertes f(x) führen, d.h. insbs., dass in den Funktionswerten keine Sprünge auftreten." (nach Wikipedia)
Mathematisch kann man das wie folgt formalisieren: Eine Funktion f: D ⊂ R → B ⊂ R, die einen Definitionsbereich D auf einen Bildbereich B abbildet, heißt (punktweise) stetig in x0 ∈ D, wenn zu jedem (beliebig kleinen) ε > 0 ein δ > 0 existiert, so dass für alle x in einer δ-Umgebung von a, d.h. ∀x: x ∈ D ∧ |x - x0| < δ gilt: der Funktionswert f(x) liegt in einer ε-Umgebung von f(x0), d.h. |f(x) - f(x0)| < ε.
Im Falle eines Sprunges bei x0 scheitert die Wahl eines beliebig kleinen ε > 0.
Ein äquivalentes Konzept ist das topologische Stetigkeitskonzept.
Es gibt neben dieser punktweisen Stetigkeit auch andere Definitionen, die insbs. in der (komplexen) Funktionentheorie sowie in der Funktionalanalysis Anwendung finden.
Re: Stimmt meine Intuition zur Stetigkeit?
Verfasst: 5. Jan 2016, 14:57
von Pippen
Danke. Nochmal für's Verständnis...wäre dann die Funktion f(x) = 5 stetig? Immerhin führen da Änderungen von x überhaupt nicht zur Änderungen von f(x).
Re: Stimmt meine Intuition zur Stetigkeit?
Verfasst: 5. Jan 2016, 15:07
von tomS
Ja. Natürlich.
Das kannst du selbst überprüfen:
1) Kannst du die Funktion f(x) = 5 zeichnen, ohne den Stift abzusetzen?
2) Wende den epsilon-delta-Beweis an.
Re: Stimmt meine Intuition zur Stetigkeit?
Verfasst: 5. Jan 2016, 15:28
von Skeltek
@tomS:
Sag mal was zu x=3
^^
Re: Stimmt meine Intuition zur Stetigkeit?
Verfasst: 5. Jan 2016, 16:13
von tomS
n = 3 ist eine Ausnahme, da 3 die Trinität bezeichnet, und da dass reelle quadratische Zahlenfeld zu Q[√3] die Klassenzahl Eins sowie die Diskrimante 12 hat, wobei letzteres der Zahl der Apostel entspricht.