Abenteuer-Universum

Eine weitere typ. Geschichte aus der Serie: Laie versucht sich an moderner Mathematik:

Nehmen wir eine Menge A = {x1,x2,x3} und eine Menge B = {y1,y2} und definieren eine Funktion f: A -> B, nach der gilt: x1 geht zu y1 und x2 geht zu y2. Diese Funktion müsste nun bijektiv sein, denn (alles aus wikipedia):

1. Eine Funktion ist bijektiv, wenn sie injektiv und surjektiv ist.
2. Eine Funktion ist injektiv, wenn kein y aus B mehrmals, sondern nur einmal oder keinmal von einem x aus A getroffen wird. Unsere Funktion ist dann injektiv, weil jedes y genau einmal getroffen wird.
3. Eine Funktion ist surjektiv, wenn für alle y aus B mind. ein x aus A existiert. Unsere Funktion ist dann surjektiv, weil jedes y einmal von einem x getroffen wird.
4. Dann müsste also unsere Funktion bijektiv sein, obwohl ein x (x3) übrigbleibt?!? Das widerspricht dem Bild der Paarbildung, wo immer jedes x mit einem y und umgekehrt verbunden ist.

Wo wäre da mein Fehler, oder wäre so eine Funktion etwa bijektiv?

Ich würde sagen, der Knackpunkt ist, auf welches y x3 abgebildet wird. Auf irgendein y muss es ja abgebildet werden, wenn es in der Definitionsmenge mit drin steht. (Wenn x3 eine Polstelle oder ähnliches ist, dann dürftest du es nicht mit in A aufnehmen.)
Wenn x3 auf y1 oder y2 abgebildet wird, dann ist die Abbildung surjektiv und nicht injektiv. Wenn x3 auf ein y3 abgebildet wird, wobei y3 nicht Element von {y1,y2} ist, dann ist die Abbildung bijektiv.

Ein typisches Beispiel für eine Injektion ist die Funktion .
Ein typisches Beispiel für eine Bijektion ist die Funktion .
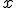
Ein typisches Beispiel für eine Surjektion ist die Funktion .

Stimmt es, dass weder injektiv noch surjektiv ist, wenn man als Definitions- und Wertemenge IR zugrunde legt?

Wo wäre da mein Fehler, oder wäre so eine Funktion etwa bijektiv?

Schau nochmal nach, wie der Begriff der Funktion definiert ist...

Stimmt es, dass x[up]2[/up] weder injektiv noch surjektiv ist, wenn man als Definitions- und Wertemenge IR zugrunde legt?

Ja, das stimmt.

breaker hat geschrieben: Schau nochmal nach, wie der Begriff der Funktion definiert ist...

Und was ist, wenn wir statt "Funktion" einen allgemeineren Begriff einsetzen, wie Relation. Wäre diese Relation des Ausgangsbeitrags dann bijektiv?

Schauen wir mal. Eine Relation zwischen zwei Mengen A und B ist per Definition eine Teilmenge des kartesischen Produktes. In Zeichen:
R ist eine Relation, genau dann wenn .

In Deinem Beispiel ist A={x[down]1[/down],x[down]2[/down],x[down]3[/down]}, B={y[down]1[/down],y[down]2[/down]}. Damit haben wir erstmal

.

Deine Relation ist nun

.

Eine Relation heißt bijektiv, wenn jedes Element von B genau einen Partner in A hat (siehe hier: http://de.wikipedia.org/wiki/Relation_%28Mathematik%29 )
Das heißt, wir müssen zwei Sachen checken:
1. Gibt es zu jedem y[down]i[/down]∈B ein mindestens Paar in R, das y[down]i[/down] als zweite Komponente hat?
2. Gibt es zu jedem y[down]i[/down]∈B ein höchstens Paar in R, das y[down]i[/down] als zweite Komponente hat?

Zu 1.: B hat die Elemente y[down]1[/down] und y[down]2[/down]. Zu y[down]1[/down] haben wir in R das Paar (x[down]1[/down],y[down]1[/down]), das offensichtlich y[down]1[/down] als zweite Komponente hat. Für y[down]2[/down] genau so. Also ist 1. erfüllt.
Zu 2.: Zu y[down]1[/down] gibt es offenbar nur ein einziges Paar in R, das y[down]1[/down] als zweite Komponente hat. Für y[down]2[/down] genau so. Also ist auch 2. erfüllt.

Die Relation ist also bijektiv (sie ist aber keine Funktion!)


Übungsaufgabe: Gib jeweils ein Beispiel einer Relation, die 1. bzw. 2. nicht erfüllt.

breaker hat geschrieben: Die Relation ist also bijektiv (sie ist aber keine Funktion!)

Aber das heißt, dass die Darstellung der Bijektion als 1:1 Paarbildung falsch ist. Ich dachte bisher immer, Bijektion ist sowas wie wenn jeder Stuhl mit genau einer Person besetzt ist. Nun merke ich, dass auch bei einer Bijektion "was übrig bleiben kann". Vllt. brauchen wir sowas wie eine Überbijektion dafür^^.

Das Attribut "surjektiv" steht völlig ohne Kontext, wenn man nicht bereits vorher die Zielmenge festlegt, in dem die Bildmenge liegt.
Bezüglich der eigenen Bildmenge ist jede Funktion surjektiv. Bildet man durch f(x)=2x die Menge A={1,2} auf B={2,4} ab, ist das surjektiv.
Ohne zu wissen, ob in der Zielmenge weitere Elemente enthalten sind(genauer gesagt sein sollen), ist eine Feststellung ob die Abbildung surjektiv ist gar nicht möglich.

Pippen hat geschrieben:

breaker hat geschrieben: Die Relation ist also bijektiv (sie ist aber keine Funktion!)

Aber das heißt, dass die Darstellung der Bijektion als 1:1 Paarbildung falsch ist. Ich dachte bisher immer, Bijektion ist sowas wie wenn jeder Stuhl mit genau einer Person besetzt ist. Nun merke ich, dass auch bei einer Bijektion "was übrig bleiben kann". Vllt. brauchen wir sowas wie eine Überbijektion dafür^^.

@breaker: was genau meinst du damit, dass eine bijektive Relation keine Funktion ist?
@Pippen: deine Vorstellung ist m.E. schon richtig; es kann nichts "übrig bleiben"; wie soll das gehen?

@breaker: Gehst du davon aus, dass eine Funktion über eine inkontinente abzählbare Menge das Ergebniss anhand von arithmetischen Kriterien determiniert?
Funktion im mathematischen oder technischen Sinne?

tomS hat geschrieben:@breaker: was genau meinst du damit, dass eine bijektive Relation keine Funktion ist?

Naja, Pippens Relation ist keine Funktion, weil sie x[down]3[/down] nicht abbildet.

tomS hat geschrieben:@Pippen: deine Vorstellung ist m.E. schon richtig; es kann nichts "übrig bleiben"; wie soll das gehen?

Weil halt Bijektivität für Relationen ein bisschen allgemeiner definiert ist, als für Funktionen.

Pippen hat geschrieben:Aber das heißt, dass die Darstellung der Bijektion als 1:1 Paarbildung falsch ist. Ich dachte bisher immer, Bijektion ist sowas wie wenn jeder Stuhl mit genau einer Person besetzt ist. Nun merke ich, dass auch bei einer Bijektion "was übrig bleiben kann". Vllt. brauchen wir sowas wie eine Überbijektion dafür^^.

Für eine bijektive Funktion ist dieseVorstellung richtig, für eine bijektive Relation nicht. So einfach ist das.

@breaker:
Die Bildmenge einer Relation besteht doch nur aus wahr und falsch?
entweder ein Paar steht in Relation oder es tut es nicht.

Was du meinst sind rechtstotal und linkseindeutig (injektiv und surjektiv sind soweit ich das jetzt glaube nur "Hilfsadjektive" zur simplifizierten Erklärung).
Ein Elementpaar (a,b) steht je nach definition in Relation zueinander oder tut es nicht.
Das ist eigentlich eine Abbildung nach wahr und falsch.
Eine Relation "R(a,b)" ist ein Element der Urbildmenge, nicht die Abbildung selbst.
So sind dann "wahr" und "falsch" Elemente der Bildmenge.

Sorry, hatte deinen Beitrag beim ersten mal nur flüchtig angeschielt
Aber was du schreibst ist sonst völlig richtig.
Man kann es noch anders darstellen indem man sagt, dass A in Relation zu B steht genau dann, wenn der Funktionswert von A das B ist.

Könnte sich bitte jeder schnell den Wikipedia-Artikel:
http://de.wikipedia.org/wiki/Relation_%28Mathematik%29
durchlesen, bevor er seinen Senf dazu gibt? Das würde einiges vereinfachen...