Leben im Kosmos

Nach dem kosmischen Standardmodell hat sich die Materie bereits etwa 1 MiIlion Jahre (10⁶ J) nach dem so genannten Urknall zu ersten Galaxien formiert. Die physikalischen Bedingungen in diesen frühen Galaxien erlaubten aber noch nicht die Entwicklung lebensfähiger Systeme, da diese frühen Galaxien fast ausschließlich nur aus Wasserstoff und Helium bestehen konnten. Die Entwicklung lebensfähiger Bedingungen in den Galaxien benötigte nach dem Stand unserer heutigen Erkenntnisse wahrscheinlich weitere 1 bis 2 Milliarden Jahre. Durch atomare Fusionsvorgänge und radioaktiver Zerfälle schwerer Atomkerne müssen sich erst genügend atomare Lebensbausteine (Kohlenstoff, Sauerstoff, Stickstoff, Schwefel, Eisen, Natrium, Kalium, Magnesium, Halogene und Spurenelemente) anreichern. Die Wechselwirkungen in diesen frühen Galaxien waren sicherlich außerordentlich turbulent. Erst aus den Trümmern der ersten sehr kurzlebigen Sterne konnten Sterne mit einer genügend hohen Lebensdauer von einigen Milliarden Jahren entstehen, die für die Entwicklung von Leben genügend Zeit boten und an der Oberfläche ihrer Trabanten ausreichend atomare Lebensbausteine hatten. Unter Verallgemeinerung der Bedingungen wie das Leben auf der Erde entstand, benötigt ein System 2 bis 3 Milliarden Jahre bis zur Bildung der ersten primitiven zellulären Lebensformen. Demnach konnten im frühen Kosmos erste Lebensspuren erst 3 bis 5 Milliarden Jahre nach dem Urknall auftreten. Die Evolution des Lebens beansprucht danach ungefähr weitere 2 Milliarden Jahre bis zur Bildung einer Zivilisation. So könnten die ersten Zivilisationen den Kosmos frühestens 5 bis 7 Milliarden Jahre nach dem Urknall bevölkert haben. Schätzt man das Alter des Kosmos auf ungefähr 15 Milliarden Jahre, so könnte es 8 bis 10 Milliarden Jahre vor unserer Zeit schon etliche Zivilisationsgenerationen gegeben haben, die bereits wieder vergangen sind. Altersangaben des Kosmos wie 13,6 Milliarden Jahre täuschen eine Genauigkeit vor, die es bislang nicht gibt, denn jede dieser Schätzungen ist mit einer Unsicherheit von mehreren Milliarden Jahren behaftet.

Wie groß könnte das Zeitfenster sein, in dem Zivilisationen gleichzeitig im Kosmos oder in einer Galaxie existieren können? Die Breite dieses Zeitfensters hängt im Wesentlichen von 3 Faktoren ab, der Zeit die klimatisch ein System für die Existenz von Leben bietet, der Entwicklungsdauer einer Zivilisation und der Lebensdauer einer Zivilisation. Wir können hier nur von den Bedingungen ausgehen, wie sie in unserem eigenen Sonnensystem bestehen. Man schätzt, dass die Energieproduktion der Sonne ungefähr weitere 3 Milliarden Jahre wie zum gegenwärtigen Zeitpunkt anhalten wird. Eine Zivilisation benötigt zu ihrer Entwicklung aus atomaren Lebensbausteinen etwa 4 bis 5 Milliarden Jahre. Prinzipiell kann eine Zivilisation maximal über die gesamte Breite des Zeitfensters bestehen bleiben. Das Alter unseres Sonnensystems wird auf 4,5 bis 5 Milliarden Jahre geschätzt. Aus diesen Zahlen lässt sich ein Zeitfenster zu 3,25 ± 0,75 Milliarden Jahre ableiten, in dem Zivilisationen gleichzeitig im gesamten Kosmos oder in einer Galaxie bestehen können. Das Zeitfenster wäre also groß genug, dass sich jede derzeit lebende Zivilisation innerhalb einer Galaxie untereinander mit Radiosignalen erreichen kann. Die Evolutionsgeschwindigkeit der menschlichen Zivilisation aus einer potentiell entwicklungsfähigen Art betrug minimal nur etwas mehr als 5 Millionen Jahre. Sollte eine Zivilisation vorzeitig zugrunde gehen, so kann sich aus einer entwicklungsfähigen völlig anderen Art innerhalb des gleichen Zeitfensters eine neue Zivilisation bilden. Es ist sogar denkbar, dass auf einem Planeten mehr als eine Zivilisation bestehend aus völlig unterschiedlichen Arten wie auch Organisationsstufen nebeneinander vorkommen können, zum Beispiel eine rein marine und eine rein terrestrische Zivilisation.

FRANK DRAKE, ein US-Astronom und Astrophysiker ist Gründer des Seti-Projekts, das sich mit der Suche nach außerirdischen Signalen befasst. Im Jahr 1961 stellte er die bis heute nicht genau lösbare Drake-Gleichung vor. Seine Gleichung fand ich im Internet auf der Homepage eines gewissen "MATTHIAS", dessen Darstellung der Gleichung sei weiter unten dargeboten. Die Gleichung enthält tatsächlich Parameter, die kaum verifizierbar sind. So ist zum Beispiel die Lebensdauer einer Zivilisation kaum bestimmbar, da es dafür keinerlei Vergleichsdaten gibt und die auch durch keine Methode in Erfahrung zu bringen sind. Wie bereits oben bemerkt, kann sich die Lebensdauer einer Zivilisation über das gesamte Zeitfenster erstrecken oder nur einen Bruchteil davon ausmachen. Ebenso ist der Faktor technisch ausreichend entwickelter Zivilisationen praktisch nicht zu determinieren. Auch ist der Faktor R nach meinem Empfinden ziemlich unklar definiert, was unter der "Bildungsrate" geeigneter Sterne zu verstehen ist. Diese Gleichung dient lediglich dazu Zivilisationen abzuschätzen, die auf einen ähnlichen technischen Entwicklungsstand stehen wie unsere menschliche Zivilisation.

Die Drake-Gleichung:

Eine andere Darstellungsform ist:

Kurzbeschreibung:

N, A: Anzahl technischer Zivilisationen in unserer Milchstraße, die Radiosignale empfangen können
R: Bildungsrate geeigneter Sterne
Z*: Zahl der Sterne in unserer Galaxie
A_s: Anteil der Sterne, die für Planetensysteme geeignet sind
f(p), Z_p: Anteil der Sterne (zu R) mit Planetensystemen
n(e), Z_e: Anzahl / Anteil der Planeten in einer lebensfähigen Zone
f(l), A_l: Anzahl / Anteil der Planeten (zu n(e) und Ze) auf denen sich Leben entwickelt
f(i), A_i: Anzahl / Anteil der Planeten, auf denen sich intelligentes Leben entwickelt
f(c), A_k: Anteil der Planeten mit technologisch ausreichend entwickelten Zivilisationen, die kommunikationsfähig sind
L: Lebensdauer einer solchen Zivilisation

Ohne die Drake-Gleichung vorher gekannt zu haben, entwarf ich vor einem Jahr eine Gleichung mit einer anderen Zielsetzung als die der Drake-Gleichung. Diese Gleichung ähnelt zwar der Drake-Gleichung, weicht aber in einigen Punkten wesentlich davon ab. Sie will lediglich abschätzen, wie viel Zivilisationen gleich welcher Kulturstufe es im selben Zeitfenster einer Galaxie geben könnte. Ihre Parameter sind, wie ich meine, auch etwas leichter zu bestimmen als die der Drake-Gleichung. Sie sei hier in einer überarbeiteten Version besprochen.

Von den S in Frage kommenden Sternen (alle Sterne der sogenannten Ökozone) einer Galaxie haben vielleicht X₁ eine ähnliche Lebensdauer wie unsere Sonne, also ungefähr S∗X₁ Objekte. Von diesen S∗X₁ Objekten besitzen vielleicht wiederum nur X₂ ein Planetensystem, also S∗X₁∗X₂ Objekte. Von diesen S∗X₁∗X₂ Objekten mit einem Planetensystem besitzen abermals vielleicht nur X₃ einen Gesteinsplaneten ähnlich unserer Erde, also S∗X₁∗X₂∗_X3 Objekte. Wieder umkreisen von diesen Gesteinsplaneten mutmaßlich nur X₄ das Zentralgestirn im richtigen Abstand, so dass sich auf ihnen Leben entwickeln kann, also S∗X₁∗X₂∗X₃∗X₄ Objekte. Auf diesen Objekten verlief die Evolution ebenfalls in nur X₅ der Fälle ähnlich wie auf unserer Erde, also S∗X₁∗X₂∗X₃∗X₄∗X₅ Objekte. Last not least konnte sich auf diesen Objekten wiederum in nur X₆ der Fälle eine Zivilisation entfalten, also S∗X₁∗X₂∗X₃∗X₄∗X₅∗X₆ Objekte. Daraus leitet sich eine Formel für die Anzahl Y der Zivilisationen einer beliebigen Galaxie ab.

Unter Annahme eines durchschnittlichen Reduktionsfaktors ändert sich die Formel in:

=(X₁∗X₂∗X₃∗X₄∗X₅∗X₆)^1/6=(Y/S)^1/6

Y=S∗⁶

Wobei S die Gesamtzahl der Sterne ist, die sich im biogenen Bereich (Ökozone) einer Galaxie befinden und 1≥>0 ist (Reduktionsfaktor). Jedes X_i genügt der Ungleichung 1≥X_i>0, da jedes X_i ein Reduktionsfaktor für den vorausgegangenen Ausdruck ist, sollte man die Formel vielleicht besser als Klammerausdruck darstellen:

X₁ ist die Größenordnung für den Anteil sonnenähnlicher Sterne unter Einbeziehung von weißen Zwergen, die ja wahrscheinlich dem Endzustand eines sonnenähnlichen Sternes entsprechen, könnte dieser Wert in der Nähe von 0,5 (0,2 nach Information aus Internet) liegen. Setzt man voraus, dass sonnenähnliche Sterne aus Trümmern explodierter Sterne und interstellarer Staub- und Gaswolken, die sich überwiegend aus Wasserstoff zusammensetzen, entstehen, könnten die Werte für X₂ und X₃ sogar zwischen 1 und 0,5 liegen. In unserem Sonnensystem umkreisen sogar 3 Planeten die Sonne in der sogenannten biogenen Zone. Allerdings hat sich nur auf einem dieser Planeten nachweislich Leben entwickelt. Der Wert für X₄ wäre daher zwischen 0,5 und 0,1 anzunehmen. Unter der Annahme, dass die Entwicklung der Materie über abiogen entstandene organische Bausteine zu lebender Materie ein universelles Prinzip ist, liegt der Wert für X₅ sogar nahe 1. Die Evolution des Lebens muss nicht zwangsläufig zu einer Zivilisation führen. Der Wert für X₆ könnte deshalb sehr nahe bei 0 liegen.

Der Durchschnittswert _1-5 für die Parameter von X₁ bis X₅ lässt sich einigermaßen zuverlässig aus dem Wert für X₆ abschätzen. ist gleich:

= (Y/S)^1/6

Extrapoliert man aus dieser Gleichung X₆ so ergibt sich für _1-5:

_1-5 = (Y/(S∗X₆))^1/5

Im Nachhinein werde ich mich nur noch auf unsere eigene Galaxie beschränken. Nach neueren Angaben besteht sie aus etwa 300 Milliarden (3 x 10¹¹) Sternen, 2/3 davon mögen in der sogenannten Ökozone der Galaxie vorkommen, also ungefähr 200 Milliarden (S = 2 x 10¹¹). Angenommen wir wären die einzige Zivilisation in dieser Galaxie (Y = 1), was ich allerdings für sehr unwahrscheinlich halte, so errechnet sich der Durchschnittswert zu 0,013. Nimmt man weiterhin an, die Chancen für die Entwicklung einer Zivilisation lägen nur bei 1 Promille, also X₆ = 0,001, so errechnet sich der Durchschnittswert _1-5 zu etwas größer als 0,021. Setzt man 0,02 für den Durchschnittswert ein, so könnte es in dieser Galaxie außer der unseren immerhin noch 12 andere Zivilisationen geben und nicht nur eine. Setzt man statt dessen 0,022 für ein, so vergrößert sich die Zahl der Zivilisationen auf 23. Ich halte diese Werte für die allerunterste Grenze.

Da es sich um Milliarden Objekte handelt, kann man darauf mit Fug und Recht die Gesetze der großen Zahl anwenden, mit anderen Worten die Wahrscheinlichkeitsrechnung. Denn es ist durchaus möglich auch für eine völlig unbekannte Stichprobe das Wahrscheinlichkeitsmaximum zu bestimmen.
Unterstellt man der Durchschnittswert sei aus einer unbekannten Messreihe beziehungsweise Stichprobe entstanden, dann unterliegt er einer bestimmten statistischen Verteilungsform. In Betracht kämen 2 Verteilungen, nämlich die Normalverteilung und die logarithmische Normalverteilung. Bekannt ist uns nur der Minimalwert von = 0,013, formal läge der Maximalwert von bei 1, was aber mit Sicherheit absolut falsch ist, deshalb setze ich den Maximalwert für analog der obigen Betrachtung willkürlich auf 0,1 fest. Das Wahrscheinlichkeitsmaximum für liegt dann irgendwo zwischen 0,013 und 0,1. Nach der Normalverteilung ist dann das Wahrscheinlichkeitsmaximum für = 0,0435 mit einer Wahrscheinlichkeitsdichte von aufgerundet 0,4 (nach der standardisierten Normalverteilung). Auf unsere Galaxie bezogen errechnet sich danach ein Wert von immerhin 1355 Zivilisationen. Nach der logarithmischen Normalverteilung wäre das Wahrscheinlichkeitsmaximum für = 0,036. Das ergäbe immer noch einen Wert von 435 Zivilisationen. Gegenüber der Normalverteilung ist das Wahrscheinlichkeitsmaximum für bei der logarithmischen Normalverteilung nach links verschoben (weil unsymmetrisch links schräg). Für eine euphorische Schätzung des Wahrscheinlichkeitsmaximums von müsste man den Maximalwert mit der Wahrscheinlichkeit 0,000000000005 (1/S) zulassen. Der untere Eckwert von = 0,013 hat übrigens ebenfalls die gleiche Wahrscheinlichkeit von nur 0,000000000005 (1/S). Für diese Wahrscheinlichkeiten (f(c)) ist nach der standardisierten Normalverteilung die Variable c fast genau ±7. Danach läge nach der Normalverteilung das Wahrscheinlichkeitsmaximum von bei fast 0,5 (folglich Y = 2,889∗10⁹) und nach der logarithmische Normalverteilung bei 0,114 (folglich Y = 438994). Sofern der oben angegebene Wert für X₁ von 0,2 in der richtigen Größenordnung liegt, errechnet sich der maximale - Wert aufgerundet zu 0,765, der untere Eckwert von 0,013 bleibt natürlich erhalten. Für beide Eckwerte erhöht sich die Wahrscheinlichkeit f(c) von 0,000000000005 auf 0,000000000025, also um das 5-fache. Nach der Normalverteilung läge dann das Wahrscheinlichkeitsmaximum von nur noch bei 0,376 (folglich Y= 5,65∗10⁸) und nach der logarithmischen Normalverteilung bei 0,0997 (folglich Y= 196427). Unter der Zuweisung von bestimmten maximalen und minimalen Eckwerten ließe sich dieses Verfahren auch für jeden einzelnen Parameter von X_i anwenden und praktisch endlos fortsetzen.

Ich will hier aber die Berechnungen abbrechen, denn es zeichnet sich ab, je genauer man die Eckwerte nach der Wahrscheinlichkeitsrechnung abgrenzt, umso mehr verschiebt sich Y (Anzahl der Zivilisationen) deutlich nach unten. Ich halte deshalb den Wert für unsere Galaxie Y= 1000 ± 500 wahrscheinlichkeitstheoretisch noch am besten untermauert. Das Wahrscheinlichkeitsmaximum von liegt dabei zwischen 0,0368 und 0,0442 für beide Verteilungen. Die oberen Eckwerte von sind dagegen für beide Verteilungen verschieden: für die Normalverteilung zwischen 0,0866 und 0,1014 und für die logarithmische Normalverteilung etwas höher zwischen 0,1042 und 0,1503.

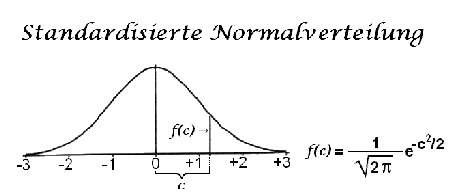
Nachtrag: Trägt man die Schätzung Y= 1000 ± 500 in das Diagramm der standardisierten Normalverteilung so ein, dass für die Werte Y= 500 und Y= 1500 f(c) = 0,19947 und für Y= 1000 f(0) = 0,39894 sind, erhält man folgendes Diagramm:

W(Y=1000 ± 500) ist die Wahrscheinlichkeit des Intervalls von Y= 500 bis Y= 1500. Für die Zuweisung eines Y-Wertes zu einer bestimmten Wahrscheinlichkeitsdichte von f(c) teilt man zweckdienlich Y in Y₁ für Werte kleiner als 1000 und Y₂ für Werte größer als 1000. Es soll gelten f(-c) = 0,39894∗(Y₁/1000) = f(+c) und der entsprechende Y-Wert im positiven Bereich von c sei Y₂= (10002/Y₁)-Y₁ beziehungsweise f(+c) = 0,39894∗1000/(Y₁+Y₂) = f(-c). Man kann aber auch dieser Rechnung vorwerfen, dass sie im Prinzip rein spekulativ sei, weil sie auf nicht beweisbare Annahmen beruht.

Fazit:
Die Beschäftigung mit der Normalverteilung brachte mich auf die Idee, eine rein statistisch-mathematische von nicht beweisbaren Annahmen freie Schätzung vorzunehmen. Das zugrunde liegende Prinzip ist, von einer unbekannten Menge gleichartiger Objekte sei nur ein Objekt bekannt, dem wir die höchste Wahrscheinlichkeitsdichte von f(c) = f(0) zuweisen. Alle anderen Zahlen (Y) aus dieser unbekannten Menge haben konform der Normalverteilung eine geringere Wahrscheinlichkeitsdichte von f(c)= f(0)/Y, also Y= f(0)/f(c). Eine zuverlässige Schätzung ist, wenn man nur 1% Irrtumswahrscheinlichkeit annimmt, also die Wahrscheinlichkeit W= 0,99 ist. Der dazugehörige c-Wert ist c = ± 2,576, wobei die letzte Dezimale durch lineare Interpolation ermittelt wurde und f(± 2,576) = 0,00577 (aufgerundet) ist, also dafür Y=69. Demnach ist nach einer zuverlässigen "drakefreien" Schätzung die Anzahl der Zivilisation in unserer Galaxie nur Y=35 ± 34 mit einer Wahrscheinlichkeit von W= 0,99, also wesentlich geringer als alle anderen Spekulationen - aber vielleicht etwas zuverlässiger.

Also mathematisch korrekt formuliert ist die Wahrscheinlichkeit, dass es in unserer Galaxie 1 bis 69 Zivilisationen geben könnte, gleich:

Und die Wahrscheinlichkeit, dass es mehr als 69 Zivilisationen geben könnte, gleich:

Außerdem habe ich es unterlassen, den Unterschied zwischen Wahrscheinlichkeitsdichte (w) und Wahrscheinlichkeit (W) zu erklären. Für die standardisierte Normalverteilung ist die Wahrscheinlichkeitsdichte gleich dem Funktionswert von c (w=f(c)) und die Wahrscheinlichkeit das bestimmte Integral über einen c-Bereich der Funktion, so zum Beispiel ist das bestimmte Integral von c = -2,576 bis c = +2,576 W=0,99 und von c minus unendlich bis c plus unendlich W = 1. Und noch etwas für den Genauigkeitsfanatiker: in der Gleichung Y = f(0)/f(c) ist f(c) eigentlich mit einem Korrekturfaktor Epsilon zu multiplizieren, den ich oben willkürlich auf 1 gesetzt habe. Wählt man Epsilon kleiner als 1, so erhöht sich die Zahl der möglichen Zivilisationen Y, und für Epsilon größer als 1 verkleinert sich die Zahl Y. Wollte man damit beweisen, dass wir nur die derzeit einzige lebende Zivilisation in dieser Galaxie sind W(Y = 1) = 0,99, so müsste Epsilon auf größer als 34,6 (exakt 34,5702) gesetzt werden. Damit erscheint es wahrscheinlicher, dass wir eben nicht die einzige derzeit lebende Zivilisation in dieser Galaxie sind, was letztendlich reine Glaubenssache ist, weil es exakt nicht zu beweisen ist.

Benutzte Quellen:
1) Drake-Gleichung aus Internet
2) Documenta Geigy, Wissenschaftliche Tabellen