Danke! Ich denke das hilft weiter.
Phasenraum ist im Prinzip klar.
Das Prinzip der Fourierzerlegung auch: Man kann ein beliebiges, periodisches Signal (z.B. ein Rechtecksignal) in eine Reihe von Sinus/Cosinusschwingungen zerlegen.
Was mich etwas verwirrt ist, dass wir mal im Kasten sind und mal nicht. Breaker war eigentlich noch nicht so weit.
tomS hat geschrieben:Am Beispiel eines Teilchens in einem eindimensionalen Kasten - was einer eingespannten Saite entspricht - sehen wir, dass als erlaubte Impulseigenzustände nur diskrete Werte p = k/L möglich sind (k ist eine ganze Zahl).
Dies folgt einfach aus den Randbedingungen bei x=0 und x=L wo die Saite ei gespannt ist.
Das ist aber soweit klar: Im Kasten können nur Schwingungen existieren, die ihre Knoten an den Kastenwänden haben. Daraus ergeben sich die erlaubten Wellenlängen im Kasten.
tomS hat geschrieben:Die Basis des Vektorraumes wird in diesem speziellen Fall durch die Funktionen {1, exp(ix), exp(2ix), ..., exp(ikx), ...} gebildet.
... woraus sich dann auch die Dimensionen/Koordinatenachsen ergeben, für die Grundschwingung eine und für jede mögliche Oberschwingung eine, unendlich viele.
Nebenfragen:
Ich könnte im Prinzip ja auch statt einen Vektor in einen unendlich-dimensionalen Vektorraum einzuzeichnen auch unendlich viele Vektoren in einen endlich-dimensionalen Vektorraum einzeichnen. Das sollte äquivalent sein. Die Hilbertraumdarstellung ist also quasi eine Zusammenfassung von unendlich vielen Zeigern zu einem einzigen? Ja?
Und:
Wenn nur die 1. Schwingung existieren würde, dann würden sich die notwendigen Dimensionen zur Darstellung auf 1 (für x) reduzieren?
Wie ist das dann, wenn ich nicht im Kasten wäre und ich einen Sinus vorliegen hätte?
Siehe auch unten zu deltaxp: Ich vermute ein einzelner Sinus ist nicht möglich. Ist das so?
Frage:
Ist die Wellenfunktion dann eine Projektion der Bewegung des Vektors im Hilbertraum, so ähnlich, wie ein Sinus eine Projektion eines rotierenden Vektors im Einheitskreis ist?
deltaxp hat geschrieben:ein quantenmechanisches teilchen ist kein klassisches teilchen, welches wir in unser welt mit den 6 kooridinaten des phasenraumes (3x ort, 3x impuls) beschreiben können. es ist i.a. ein wellenpaket. ein wellenpakeet hat sicher einen mittleren impuls (Gruppengeschwindigkeit) und einen mittleren ort (den man klassisch als phasenraumkoordinaten verwendet) aber du kannst nicht sagen, dass ein wellenpaket DEN ort und DEN impuls hat, es ist über viele orte verschmiert und besteht aus vielen grundwellen, die alle ihre eigenen impulse (phasengeschwindigkeiten) haben.
...und deshalb ist ein Teilchen immer ein Wellen
paket, also eine Überlagerung aus unendlich vielen verschiedenen Wellenlängen; denn entspräche es nur einer Welle, mit genau einer Wellenlänge, dann wäre sein Impuls völlig scharf, was wegen der Unschärferelation ausgeschlossen ist?
deltaxp hat geschrieben:...weil wenn sich ein zeiger bewegt, bleibt die länge des zeigers konstant
Hatte ich schon so gedacht, ist aber wichtig es nochmals zu sagen. Daher die Normierung.
deltaxp hat geschrieben:wichtig ist vielleicht noch zu erwähnen: um sicher zu sein, dass die länge des zeigers endlich ist muessen in einem unendlichdimensionalen raum natürlich die die beträge der koordinaten in den hohen diemensionen immer kleiner werten so dass die die summer über sie endlich (und auf 1 noriert ist).
D.h. wenn ich den Zeiger im Hilbertraum in einer anderen Darstellung in viele Zeiger zerlegen würde, dann würden die hochdimensionalen Zeiger immer kürzer werden.
Die Summe aller Zeiger müsste exakt 1 ergeben.
Außerdem muss in der Hilbertraumdarstellung sichergestellt sein, dass das auch so (zu 1) konvergiert?
deltaxp hat geschrieben:was sind das für transformationen die die eine vektorlänge konstant lassen, sozusagen nur seine richtung verändern: drehungen
Warum nicht auch Translationen?
deltaxp hat geschrieben:und die zeitliche entwicklung kann man durch einen operator beschreiben dass ist
=e^{iHt})
(und der muss eben unitär sein, damit die norm erhalten bleibt: U*U=1)
Heißt das, dass die Länge des Zeigers sozusagen die Anzahl der betrachteten Objekte darstellt - und die muss bei einem betrachteten Objekt, das auch genau eine Objekt bleibt eben immer 1 sein? Vielleicht sollte man auch sagen, dass die Länge des Zeigers die Wahrscheinlichkeit darstellt ein Objekt zu finden - und die muss 100% = 1 sein?
Der Operator sagt uns, wie sich der Zeiger bewegt. Das Problem dabei ist, dass das Kommutativgesetz nicht erfüllt ist, wenn ich zwei Operatoren hintereinander ausführe.
Daher brauche ich die Kommutatoren, die mir die Abweichung vom kommutieren angeben.
@breaker:
Ab da versteh ich's noch nicht ganz:
breaker hat geschrieben:Nun sind wir endlich in der Lage zu sagen, was "Quantisierung" bedeutet.
Ein physikalisches System zu
quantisieren bedeutet, einen (geeigneten) Hilbertraum

zu finden und allen klassischen Observablen
)
Operatoren
)
auf diesem Hilbertraum zuzuordnen, sodass fuer je zwei Observablen

gilt:
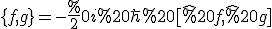
.
D.h. grob gesagt macht man aus Poissonklammern Kommutatoren. Beispielsweise muss man also fuer
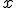
und

Operatoren

finden, sodass
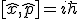
(da {x,p}=1 war).
Wo ist der Kommutator?
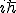
?
Was passiert da? Muss ich die Operatoren mit den Kommutatoren verrechnen, damit das Kommutativgesetz quasi erfüllt wird? Darf ich das?
Was, wenn ich das Kommutativgesetz ignoriere? Wenn ich meinen Zeiger mit nur einem Operator bewege, ist das dann nicht egal?
breaker hat geschrieben:Observablen sind Eigenwerte von Operatoren. Insbesondere der Ort eines Teilchens ist also immer irgendein Eigenwert des Ortsoperators.

Komprimierte Information.
Ich versuche das auf Deutsch zu verstehen:
Messgrößen sind Streckungsfaktoren eines Vektors (dessen Richtung durch eine Abbildung unverändert bleibt) bei einer Abbildung im Hilbertraum, der für jede mögliche Wellenlänge Dimensionen (z.B. zwei? Eine für Ort und eine für Impuls?) bereitstellt...?
Insbesondere der Ort eines Teilchens ist also immer eine Streckung bei einer Abbildung eines Vektors?
Nun muss aber der Einheitsvektor im Hilbertraum immer gleich lang bleiben.
Bin verwirrt. Ist ein Operator nun eine Abbildungsvorschrift oder ein Vektor? Wie kann eine Abbildungsvorschrift gestreckt werden?
Grüße
seeker


