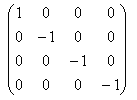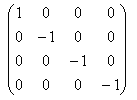Beitrag
von tomS » 19. Feb 2008, 23:14
Ich denke, durch die imaginären Zahlen in den Komponenten bzw. Basisvektoren entsteht ausschließlich Verwirrung. Ich hatte mir überlegt, das zu erwähnen, hab's aber bleiben lassen, weil es schlichtweg nichts bringt. Es ist nur ein Trick, wie man das "-" auf Kosten eines "i" los wird. Wenn man das eine nicht versteht, dann versteht man aber auch das andere nicht. Also lassen wir's bitte bleiben.
Man kann grundsätzlich über Basisvektoren reden und dies tut man auch häufig in der ART mit gekrümmter Raumzeit. Da bieten sie teilweise einen echten Vorteil bzw. es gibt teilweise Gründe, warum man sie sogar einführen muss. Allerdings ändert sich an der Argumentation mit dem "-" in der Metrik rein gar nichts; auch hier kann man die Basisvektoren reell wählen und auf den Trick mit dem "i" verzichten!
Ich erkläre kurz, wie man von dem metrischen Tensor auf das Linienelement bzw. die Norm kommt. Da wir in der speziellen Relativitätstheorie unterwegs sind, kann man den Metriktensor immer auf die von Breaker genannte Diagonalform bringen; ich schreibe dafür kurz
\fed\mixong_(\mu\nu)=diag(1, -1, -1, -1)
d.h. ich lasse die Nullen weg.
Der Metriktensor in dieser Form gilt unter der Voraussetzung, dass man kartesische Koordinaten nutzt; wählt man z.B. Kugelkoordinaten, so sieht er komplizierter aus, aber das betrachten wir hier nicht.
Zunächst bewegen wir uns in einer vierdimensionalen Raum-Zeit. Daher benötigen wir auch vier Koordinaten:
\fed\mixon(ct, x, y, z)
Damit können wir jeden Punkt "benennen". Jetzt möchten wir auch den Begriff der "Länge eines Vektors" bzw. den "Abstand zweier Punkte" definieren. Dazu können wir versuchen, das Betragsquadrat des Vektors zu berechnen. Üblicherweise benutzt man dazu den "n-dimensionalen Pythagoras". Dabei hat man aber eben bereits vorausgesetzt, dass die Metrik des Raumes gleich
\fed\mixondiag(1, 1, ..., 1)
ist.
Wenn man dies nicht voraussetzen kann, dann führt man explizit den Metriktensor g ein. Für die o.g. Vektoren
\fed\mixonx^\mu=(ct, x, y, z)
und die Metrik
\fed\mixong_(\mu\nu)=diag(1, -1, -1, -1)
folgt dann
\fed\mixonNorm^2(x) = x^\mu g_\mu\nu x^\nu
Berechnet man nun das rechte Produkt "Matrix g * Vektor x", so findet man
\fed\mixong_\mu\nu x^\nu = x_\mu = diag(1, -1, -1, -1) * (ct, x, y, z) = (ct, -x, -y, -z)
Und daraus erhält man
\fed\mixonx^\mu g_\mu\nu x^\nu = x^\mu x_\mu = (ct, x, y, z) * (ct, -x, -y, -z) = (ct)^2 - x^2 - y^2 - z^2
Dabei gilt immer, dass über doppelt auftretende Indizes summiert wird, also z.B.
\fed\mixonx^\mu x_\mu = x^0 x_0 + x^1 x_1 + x^2 x_2 + x^3 x_3
Wichtig ist dabei, dass statt eines "gewöhnlichen" Skalarproduktes immer das Produkt zweier verschiedener "Vektorsorten" gebildet wird. Üblicherweise sind dies Zeilen- und Spaltenvektor. Durch die Metrik mit den Plus- und Minuszeichen auf der Diagonalen muss man nun strikt zwischen beiden unterscheiden - daher auch die Notation mit einmal Index oben und einmal unten. Zunächst bedeutet der Übergang von oberen zu unteren Indizes, dass die räumlichen Komponenten ein Minuszeichen erhalten, geometrisch "leben" diese Vektoren jedoch in zwei verschiedenen Vektorräumen.
Diese Rechnungen sind also eigentlich nichts weiter als ein modifizierter Pythagoras zur Berechnung von "Längen" von Vektoren.
Nun kommen wir zum Linienelement. I.A. erhält man es, wenn man an eine beliebige glatte (keine Knicke!) Kurve in einem Punkt eine Tangente anlegt. Man kann in diesem Punkt ein Stückchen entlang der Kurve gehen und dabei den "Weg" bzw. die "Länge" ds zurücklegen. Dabei muss man wieder den modifizierten Pythagors benutzen. Das Linienelement entsteht also aus einem infinitesimalen Vektor (dem Tangentenvektor an eine Linie) unter der Benutzung derselben geometrie wie für "normale" Vektoren.
Al hat mit seinen Bemerkungen natürlich recht, aber ich habe hier versucht, das ohne Vorgriff auf die ART zu erklären. Deshalb auch noch ein Tip: Man kann viel (alles?) von der SRT verstehen, ohne viel in die Metrik selbst hineinzuinterpretieren. Man nutzt sie als Rechenhilfsmittel. Man kann dann auch rein physikalisch die Minuszeichen in der Formel
\fed\mixonx^\mu x_\mu = (ct)^2 - x^2 - y^2 - z^2
erklären. Das Linienelement benötigt man ebenfalls zunächst nicht.
Gruß
Tom
Der Wert eines Dialogs hängt vor allem von der Vielfalt der konkurrierenden Meinungen ab.
Sir Karl R. Popper