Abenteuer-Universum

positronium hat geschrieben:Naja, dass im Ergebnis ein pi steht, finde ich immer noch etwas befremdlich.

Na ja, aber du hast es doch berechnet ;-)

Man versteht das wie folgt.

Betrachte das Gaussche Integral

$\int_R dx\,e^{-ax^2}$

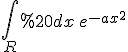
Das kann man elemenar nicht berechen, wohl aber

$\left(\int_R dx\,e^{-ax^2}\right)^2 = \int_{R^2} dx\,dy\,e^{-a(x^2+y^2)} = \int_{R^2} d^2r\,e^{-ar^2}$

Und daraus erhälst du deine Integrale in Polarkoordinaten sowie durch n-faches Ableiten nach a.

Und da man über eine rotationsinvariante Funktion exp(-ar²) integriert, bzw. wie du gezeigt hast über phi entlang einer Kreislinie, ist das Auftreten von pi nicht gar so überraschend.

tomS hat geschrieben:Na ja, aber du hast es doch berechnet

Ich kann mir doch nicht alles glauben!

tomS hat geschrieben:Betrachte das Gaussche Integral...
...über phi entlang einer Kreislinie, ist das Auftreten von pi nicht gar so überraschend.

Ja, schon.
Danke!

Und, magst du dir noch die Heisenbergsche Unschärfenrelation für|n> und |z> anschauen?

tomS hat geschrieben:Und, magst du dir noch die Heisenbergsche Unschärfenrelation für|n> und |z> anschauen?

Ja, habe ich mir für heute, nachher, aufgehoben - war mir gestern schon zu spät.

tomS hat geschrieben:Ein letztes noch: die kohärenten Zustände spielen eine Rolle in der Quantenoptik sowie in der semiklassischen Analyse verschiedener Systeme. Sie haben die Eigenschaft, Zustände minimaler Unschärfe zu sein, d.h. sie minimieren Δx*Δp. Letzteres müsstest du explizit ausrechnen können, in dem du die Definition von Δ²x aus Gl. (2.66) sowie Δ²p aus (2.67) verwendest. Dann müsstest du Δx sowie Δp durch die Erzeuger und Vernichter ausdrücken und zwischen den Zuständen sandwichen. Das kannst du einmal für <n|Δ²x|n> * <n|Δ²p|n> und einmal für <z|Δ²x|z> * <z|Δ²p|z> tun. Danach würde ich die Übingen zum Formalismus beenden, ggf. noch Fragen zur Bedeutung diskutieren und wieder im Skript fortfahren.

$\Delta^{2} x=\langle x^{2}\rangle-\langle x \rangle^{2}$
$\Delta^{2} p=\langle p^{2}\rangle-\langle p \rangle^{2}$
Dann sollte
$\Delta^{2} x=\langle \Psi|x^{2}|\Psi\rangle-\langle \Psi|x|\Psi\rangle^{2}$
$\Delta^{2} p=\langle \Psi|p^{2}|\Psi\rangle-\langle \Psi|p|\Psi\rangle^{2}$
gelten.
Dann müsste ich das, was ich in wikipedia gefunden habe

$Q=\sqrt{\frac{\hbar}{2 m \omega}}(a+a^{\dagger})$
$P=\frac{1}{i}\sqrt{\frac{m \omega \hbar}{2}}(a-a^{\dagger})$
mit x=Q und p=P einsetzen können:
$\Delta^{2} x=\langle \Psi|(\sqrt{\frac{\hbar}{2 m \omega}}(a+a^{\dagger}))^{2}|\Psi\rangle-\langle \Psi|\sqrt{\frac{\hbar}{2 m \omega}}(a+a^{\dagger})|\Psi\rangle^{2}$
$\Delta^{2} p=\langle \Psi|(\frac{1}{i}\sqrt{\frac{m \omega \hbar}{2}}(a-a^{\dagger}))^{2}|\Psi\rangle-\langle \Psi|\frac{1}{i}\sqrt{\frac{m \omega \hbar}{2}}(a-a^{\dagger})|\Psi\rangle^{2}$
Das müsste ich jetzt mit Integralen schreiben:
$\Delta^{2} x=\int dx' dx'' \Psi^{\ast}(x')\langle x'|(\sqrt{\frac{\hbar}{2 m \omega}}(a+a^{\dagger}))^{2}|x''\rangle \Psi(x'')-...$ $...\left(\int dx' dx'' \Psi^{\ast}(x')\langle x'|\sqrt{\frac{\hbar}{2 m \omega}}(a+a^{\dagger})|x''\rangle\Psi(x'')\right)^{2}$
$\Delta^{2} p=\int dp' dp'' \Psi^{\ast}(p')\langle p'|(\frac{1}{i}\sqrt{\frac{m \omega \hbar}{2}}(a-a^{\dagger}))^{2}|p''\rangle \Psi(p'')-...$ $...\left(\int dp' dp'' \Psi^{\ast}(p')\langle p'|\frac{1}{i}\sqrt{\frac{m \omega \hbar}{2}}(a-a^{\dagger})|p''\rangle\Psi(p'')\right)^{2}$
Jetzt müsste ich eigentlich vereinfachen, aber ich habe keine Ahnung, wo ansetzen. Was kann ich machen? Oder bin ich sowieso auf dem Holzweg?

Du bist auf dem richtigen Weg, machst das aber zu komplizert.

Benutze die 'normierten' Operatoren (dann fällt m, omega, usw. weg)

$a = \frac{1}{\sqrt{2}}(x+ip)$

$a^\dagger = \frac{1}{\sqrt{2}i}(x-ip)$

$H = a^\dagger a + \frac{1}{2}$

und berechnen daraus (genauso wie du es gemacht hast) x, p, sowie Δ²x und Δ²p.

Dann berechnest du die Erwartungswerte nicht zwischen allgemeinen Zuständen sondern genau für <n| ... |n> sowie <z| ... |z>; dann kannst du nämlich die Wirkung der Operatoren Δ²x und Δ²p ausgedrückt durch Erzeuger und Vernichter direkt ablesen.

D.h. du brauchst die Integrale nicht!

Dann ist
$x=\frac{1}{\sqrt{2}}(a+a^{\dagger})$
und
$p=-\frac{i}{\sqrt{2}}(a-a^{\dagger})$
Ab hier bin ich schon wieder unsicher...
$\Delta^{2} x=\langle n|\frac{1}{2}(a+a^{\dagger})^{2}|n\rangle-\langle n|\frac{1}{\sqrt{2}}(a+a^{\dagger}) |n\rangle^{2}$
$\Delta^{2} p=\langle n|-\frac{1}{2}(a-a^{\dagger})^{2}|n\rangle-\langle n|-\frac{i}{\sqrt{2}}(a-a^{\dagger}) |n\rangle^{2}$
...sollte aber so vereinfachbar sein:
$\Delta^{2} x=\frac{1}{2}(a+a^{\dagger})^{2}\left(\langle n|n\rangle-\langle n|n\rangle^{2}\right)$
$\Delta^{2} p=-\frac{1}{2}(a-a^{\dagger})^{2}\left(\langle n|n\rangle-\langle n|n\rangle^{2}\right)$
Wie kann ich hier etwas ablesen?

Du darfst die Operatoren nicht aus dem Bra-Ket rausziehen! Das ist wie die Multiplikation Vektor * Matrix * Vektor

Ein Beispiel:

$\langle n| (a^\dagger + a)^2|n\rangle = \langle n| (a^\dagger)^2 + a^2 + a^\dagger a + a a^\dagger|n\rangle$

Die erste beiden Terme fallen weg, da

$\langle n| (a^\dagger)^2 |n\rangle = \langle n| \sqrt{(n+1)(n+2)}|n+2\rangle = \sqrt{(n+1)(n+2)} \langle n|n+2\rangle = \sqrt{(n+1)(n+2)} \delta_{n,n+2} = 0$

Es bleibt

$\langle n| (a^\dagger + a)^2|n\rangle = \langle n| a^\dagger a + a a^\dagger|n\rangle = \langle n| a^\dagger \sqrt{n} |n-1\rangle + \langle n| a \sqrt{n+1}|n+1\rangle \langle n| \sqrt{n}^2 |n\rangle + \langle n| \sqrt{n+1}^2|n\rangle = 2n+1$

Nach der Methode berechnest du alle Erwartungswerte

tomS hat geschrieben:Du darfst die Operatoren nicht aus dem Bra-Ket rausziehen! Das ist wie die Multiplikation Vektor * Matrix * Vektor

Ja.

Das Ersetzen ist mir nicht in den Sinn gekommen...

Aber hier kann ich nicht folgen

tomS hat geschrieben:Es bleibt

$\langle n| (a^\dagger + a)^2|n\rangle = \langle n| a^\dagger a + a a^\dagger|n\rangle = \langle n| a^\dagger \sqrt{n} |n-1\rangle + \langle n| a \sqrt{n+1}|n+1\rangle \langle n| \sqrt{n}^2 |n\rangle + \langle n| \sqrt{n+1}^2|n\rangle = 2n+1$

Also es fehlt wohl ein =, aber dann würde aus
$\langle n| a^\dagger \sqrt{n} |n-1\rangle + \langle n| a \sqrt{n+1}|n+1\rangle$
das
$\langle n| \sqrt{n}^2 |n\rangle + \langle n| \sqrt{n+1}^2|n\rangle = 2n+1$
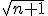
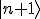
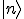
obwohl für $a^\dagger$ ... $|n-1\rangle$ das $\sqrt{n+1}$ ... $|n+1\rangle$ eingesetzt wird. Also, $|n-1\rangle$ wird dadurch zu $|n\rangle$ , aber zwischen den Vektoren sollte man dann doch $\sqrt{n+1}\sqrt{n}$ haben. Genau so müsste es doch auch nach dem Plus-Zeichen, also im zweiten Teil sein: $\sqrt{n}\sqrt{n+1}$ Oder?

Dann muss ich ab hier weiter machen.
$\Delta^{2} x=\langle n|\frac{1}{2}(a+a^{\dagger})^{2}|n\rangle-\langle n|\frac{1}{\sqrt{2}}(a+a^{\dagger}) |n\rangle^{2}$
$\Delta^{2} p=\langle n|-\frac{1}{2}(a-a^{\dagger})^{2}|n\rangle-\langle n|-\frac{i}{\sqrt{2}}(a-a^{\dagger}) |n\rangle^{2}$

Ausmultiplizieren
$\Delta^{2} x=\langle n|\frac{1}{2}\left(a^{2}+(a^{\dagger})^{2}+aa^{\dagger}+a^{\dagger}a\right)|n\rangle-\langle n|\frac{1}{\sqrt{2}}(a+a^{\dagger}) |n\rangle^{2}$
$\Delta^{2} p=\langle n|-\frac{1}{2}\left(a^{2}+(a^{\dagger})^{2}-aa^{\dagger}-a^{\dagger}a\right)|n\rangle-\langle n|-\frac{i}{\sqrt{2}}(a-a^{\dagger}) |n\rangle^{2}$

Wie in Deinem Beispiel fallen auch hier die Glieder mit quadriertem Operator heraus, weil dadurch die Bra- und Ket-Zustände unterschiedlich werden, also das Kronecker-Delta immer 0 ergibt - das ist ja der Grund.
Es bleibt:
$\Delta^{2} x=\langle n|\frac{1}{2}\left(aa^{\dagger}+a^{\dagger}a\right)|n\rangle-\langle n|\frac{1}{\sqrt{2}}(a+a^{\dagger}) |n\rangle^{2}$
$\Delta^{2} p=\langle n|-\frac{1}{2}\left(-aa^{\dagger}-a^{\dagger}a\right)|n\rangle-\langle n|-\frac{i}{\sqrt{2}}(a-a^{\dagger}) |n\rangle^{2}$

Durch Ersetzen der Operatoren sollte folgen:
$\Delta^{2} x=\langle n|\frac{1}{2}\sqrt{n}\sqrt{n+1}|n\rangle+\langle n|\frac{1}{2}\sqrt{n+1}\sqrt{n}|n\rangle-\left(\langle n|\frac{1}{\sqrt{2}}\sqrt{n} |n\rangle+\langle n|\frac{1}{\sqrt{2}}\sqrt{n+1} |n\rangle\right)^{2}$
$\Delta^{2} p=\langle n|\frac{1}{2}\sqrt{n}\sqrt{n+1}|n\rangle+\langle n|\frac{1}{2}\sqrt{n+1}\sqrt{n}|n\rangle-\left(\langle n|-\frac{i}{\sqrt{2}}\sqrt{n} |n\rangle+\langle n|\frac{i}{\sqrt{2}}\sqrt{n+1} |n\rangle\right)^{2}$

Das sollte dann
$\Delta^{2} x=\sqrt{n} \sqrt{1+n}-\left(\frac{\sqrt{n}}{2}+\frac{\sqrt{1+n}}{\sqrt{2}}\right)^2$
$\Delta^{2} p=\sqrt{n} \sqrt{1+n}-\left(-\frac{i \sqrt{n}}{\sqrt{2}}+\frac{i \sqrt{1+n}}{\sqrt{2}}\right)^2$
ergeben.

Wenn ich jetzt aber
$\left(\Delta^{2} x\right)^{2}\left(\Delta^{2} p\right)^{2}$
für den Grundzustand n=0 berechne, erhalte ich
$\frac{i}{2}$
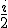
was wegen dem auf 1 gesetzten h-quer
$\frac{i}{2}\hbar$
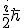
ergäbe.
Aber eigentlich müsste ja $\frac{\hbar}{2}$ heraus kommen.
Was ist falsch?

Zunächst mal fehlt tatsächloch das '='.

Zu der Fragestellung mit den Wurzeln: es gilt

$a |n\rangle = \sqrt{n}|n-1\rangle$

$a^\dagger |n\rangle = \sqrt{n+1}|n+1\rangle$

Damit ist aber

$a^\dagger a |n\rangle = \sqrt{n} a^\dagger |n-1\rangle = \sqrt{n}\sqrt{(n-1)+1}|(n-1)+1)\rangle = n|n\rangle$

Ach so. Ich hatte das vorhandene n nur im Ket berücksichtigt, und ausserhalb nicht. Danke!

Dann muss ich hier nochmal beginnen:
$\Delta^{2} x=\langle n|\frac{1}{2}\left(aa^{\dagger}+a^{\dagger}a\right)|n\rangle-\langle n|\frac{1}{\sqrt{2}}(a+a^{\dagger}) |n\rangle^{2}$
$\Delta^{2} p=\langle n|-\frac{1}{2}\left(-aa^{\dagger}-a^{\dagger}a\right)|n\rangle-\langle n|-\frac{i}{\sqrt{2}}(a-a^{\dagger}) |n\rangle^{2}$

Operatoren ersetzen, und dabei den Fehler mit den Kets im quadrierten Teil nicht nochmal machen:
$\Delta^{2} x=\langle n|\frac{1}{2}\sqrt{n+1}\sqrt{n+1}|n\rangle+\langle n|\frac{1}{2}\sqrt{n}\sqrt{n}|n\rangle-\left(\langle n|\frac{1}{\sqrt{2}}\sqrt{n} |n-1\rangle+\langle n|\frac{1}{\sqrt{2}}\sqrt{n+1} |n+1\rangle\right)^{2}$
$\Delta^{2} p=\langle n|\frac{1}{2}\sqrt{n+1}\sqrt{n+1}|n\rangle+\langle n|\frac{1}{2}\sqrt{n}\sqrt{n}|n\rangle-\left(\langle n|-\frac{i}{\sqrt{2}}\sqrt{n} |n-1\rangle+\langle n|\frac{i}{\sqrt{2}}\sqrt{n+1} |n+1\rangle\right)^{2}$

Vereinfachen (jetzt fällt der quadrierte Teil wegen <n| und |n-1> bzw. |n+1> weg):
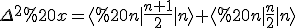
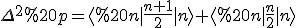
$\Delta^{2} x=\langle n|\frac{n+1}{2}|n\rangle+\langle n|\frac{n}{2}|n\rangle$
$\Delta^{2} p=\langle n|\frac{n+1}{2}|n\rangle+\langle n|\frac{n}{2}|n\rangle$

Das ergibt:
$\Delta^{2} x=\frac{1}{2}n$
$\Delta^{2} p=\frac{1}{2}n$

Hier war auch etwas falsch. Es ist ja $\Delta^{2} x=\frac{1}{2}n$ ... d.h. $\Delta x=\sqrt{\frac{1}{2}n}$ .

Für die Heisenbergsche Unschärferelation gilt dann
$\Delta x\Delta p=\sqrt{\frac{1}{2}n}\sqrt{\frac{1}{2}n}=\frac{1}{2}n$
Dann muss ich wohl n=1 setzen und h-quer einfügen, woraus sich
$\frac{1}{2}\hbar$
ergibt.

Du hast irgendwo noch einen Fehler drin, denn für n=0 muss 1/2 rauskommen; aber das ist Kleinkram, deine Rechnung sieht prinzipiell vernünftig aus.

tomS hat geschrieben:Du hast irgendwo noch einen Fehler drin, denn für n=0 muss 1/2 rauskommen; aber das ist Kleinkram, deine Rechnung sieht prinzipiell vernünftig aus.

Vielen Dank für Deine Bemühungen!

Der Fehler ist hier:
$\Delta^{2} x=\frac{1}{2}n$
$\Delta^{2} p=\frac{1}{2}n$
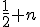
Es muss jeweils $\frac{1}{2}+n$ heissen, also + statt *.

Ergibt wiederum $\Delta x\Delta p=\sqrt{\frac{1}{2}+n}\sqrt{\frac{1}{2}+n}=\frac{1}{2}+n$

Perfekt!

So, jetzt das ganze noch für |z>. Beachte

$a|z\rangle = z|z\rangle$

$\langle z|a^\dagger = \langle z|z^\ast$

Noch etwas; es gilt natürlich |z=0> = |n=0> wie man anhand der Taylorreihe explizit sieht, aber für k = 1,2,... ist |z=k> ist etwas anderes als |n=k>, d.h. für die natürlichen Zahlen stimmen die Eigenzustände des harmonsichen Oszillators nicht mit den kohärenten Zuständen überein.

Außerdem noch interessant ist die Zeitentwicklung

$|n,t> = e^{-iHt}|n\rangle$

$|z,t> = e^{-iHt}|z\rangle$

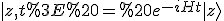
mit

$H = a^\dagger a + \frac{1}{2}$

tomS hat geschrieben:So, jetzt das ganze noch für |z>. Beachte

$a|z\rangle = z|z\rangle$

$\langle z|a^\dagger = \langle z|z^\ast$

Für x und p gilt natürlich das gleiche
$x=\frac{1}{\sqrt{2}}(a+a^{\dagger})$
und
$p=-\frac{i}{\sqrt{2}}(a-a^{\dagger})$
Eingesetzt wird in <z| |z>, weshalb folgt
$\Delta^{2} x=\langle z|\frac{1}{2}(a+a^{\dagger})^{2}|z\rangle-\langle z|\frac{1}{\sqrt{2}}(a+a^{\dagger}) |z\rangle^{2}$
$\Delta^{2} p=\langle z|-\frac{1}{2}(a-a^{\dagger})^{2}|z\rangle-\langle z|-\frac{i}{\sqrt{2}}(a-a^{\dagger}) |z\rangle^{2}$
Dann ist durch das zu ersetzen, was Du oben geschrieben hast, aber erst ausschreiben, damit ich den Überblick nicht verliere.
$\Delta^{2} x=\langle z|\frac{1}{2}(aa+a^{\dagger}a^{\dagger}+aa^{\dagger}+a^{\dagger}a)|z\rangle-\langle z|\frac{1}{\sqrt{2}}(a+a^{\dagger}) |z\rangle^{2}$
$\Delta^{2} p=\langle z|-\frac{1}{2}(aa+a^{\dagger}a^{\dagger}-aa^{\dagger}-a^{\dagger}a)|z\rangle-\langle z|-\frac{i}{\sqrt{2}}(a-a^{\dagger}) |z\rangle^{2}$
ersetzen...
$\Delta^{2} x=\langle z|\frac{1}{2}(z^{2}+(z^{\ast})^{2}+zz^{\ast}+z^{\ast}z)|z\rangle-\langle z|\frac{1}{\sqrt{2}}(z+z^{\ast}) |z\rangle^{2}$
$\Delta^{2} p=\langle z|-\frac{1}{2}(z^{2}+(z^{\ast})^{2}-zz^{\ast}-z^{\ast}z)|z\rangle-\langle z|-\frac{i}{\sqrt{2}}(z-z^{\ast}) |z\rangle^{2}$
vereinfachen...
$\Delta^{2} x=\langle z|\frac{1}{2}(z+z^{\ast})^{2}|z\rangle-\langle z|\frac{1}{\sqrt{2}}(z+z^{\ast}) |z\rangle^{2}$
$\Delta^{2} p=\langle z|-\frac{1}{2}(z-z^{\ast})^{2}|z\rangle-\langle z|-\frac{i}{\sqrt{2}}(z-z^{\ast}) |z\rangle^{2}$

Aber hier hänge ich schon wieder.
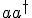
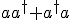
Zum einen bin ich mir nicht sicher, ob das Ersetzen von $aa^{\dagger}$ auf diese Art erlaubt ist. Sozusagen habe ich ja hier über Kreuz ersetzt, also das $a^{\dagger}$ mit <z| links von $a$ durch <z|...z*und umgekehrt. Ist dadurch die Reihenfolge verletzt? - Muss ich $aa^{\dagger}+a^{\dagger}a$ bzw. $aa^{\dagger}-a^{\dagger}a$ gar durch einen (Anti-)Kommutator ersetzen?
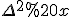
Zum anderen bin ich bei dem Quadrieren unsicher. Wenn <z| und |z> normiert sind, könnte ich $\frac{1}{\sqrt{2}}(z+z^{\ast})$ bzw. $-\frac{i}{\sqrt{2}}(z-z^{\ast})$ aus dem Skalarprodukt heraus ziehen und quadrieren, aber dann wird sowohl $\Delta^{2} x$ als auch $\Delta^{2} p$ gleich 0. Oder muss ich sowieso erst durch
$|z\rangle = e^{-|z|^2/2}\,\sum_{n=0}^\infty \frac{z^n}{\sqrt{n!}}|n\rangle$
$\langle z| = e^{-|z|^2/2}\,\sum_{n=0}^\infty \langle n|\frac{{z^\ast}^n}{\sqrt{n!}}$
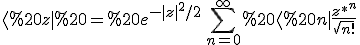
ersetzen?

Du hast einen kleinen aber wesentlichen Fehler drin

positronium hat geschrieben: $\Delta^{2} x=\langle z|\frac{1}{2}(aa+a^{\dagger}a^{\dagger}+aa^{\dagger}+a^{\dagger}a)|z\rangle-\langle z|\frac{1}{\sqrt{2}}(a+a^{\dagger}) |z\rangle^{2}$

ersetzen...

$\Delta^{2} x=\langle z|\frac{1}{2}(z^{2}+(z^{\ast})^{2}+zz^{\ast}+z^{\ast}z)|z\rangle-\langle z|\frac{1}{\sqrt{2}}(z+z^{\ast}) |z\rangle^{2}$

Es geht um

$\langle z|aa^{\dagger}|z\rangle$

Dies ist der einzige Term, wo du die Reihenfolge vertauschen musst, da |z> der Eigenzsutand zu a und nicht zu a-dagger ist.

Also

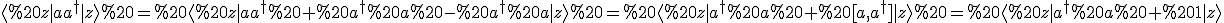
$\langle z|aa^{\dagger}|z\rangle = \langle z|aa^{\dagger} + a^\dagger a - a^\dagger a|z\rangle = \langle z|a^{\dagger} a + [a,a^\dagger]|z\rangle = \langle z|a^{\dagger} a + 1|z\rangle$

Jetzt darfst du natürlich die Operatoren durch die jeweiligen Rechts- bzw. Links-Eigenwerte ersetzen, die Eigenwerte (Zahken) aus dem Bra-Ket herausziehen und <z|z> = 1 benutzen. Durch den Kommutator bzw, die daraus entstehende Eins ist das Gesamtergebnis auch nicht mehr Null.

$\langle z|aa^{\dagger}|z\rangle = \langle z|a^{\dagger} a + 1|z\rangle = \langle z|z^\ast z + 1|z\rangle = (z^\ast z + 1) \langle z|z\rangle = z^\ast z + 1$

tomS hat geschrieben:Du hast einen kleinen aber wesentlichen Fehler drin

Es geht um

$\langle z|aa^{\dagger}|z\rangle$

Dies ist der einzige Term, wo du die Reihenfolge vertauschen musst, da |z> der Eigenzsutand zu a und nicht zu a-dagger ist.

Den Kommutator hatte ich in Verdacht, nur nicht in der Form...
Ist $\left[a,a^{\dagger}\right]$ für jeden Operator mit dem adjungierten Operator immer 1?

nochmal das Ersetzen in:
$\Delta^{2} x=\langle z|\frac{1}{2}(aa+a^{\dagger}a^{\dagger}+aa^{\dagger}+a^{\dagger}a)|z\rangle-\langle z|\frac{1}{\sqrt{2}}(a+a^{\dagger}) |z\rangle^{2}$
$\Delta^{2} p=\langle z|-\frac{1}{2}(aa+a^{\dagger}a^{\dagger}-aa^{\dagger}-a^{\dagger}a)|z\rangle-\langle z|-\frac{i}{\sqrt{2}}(a-a^{\dagger}) |z\rangle^{2}$
ergibt (bei $\Delta^{2} p$ unter Vorbehalt wegen der umgekehrten Reihenfolge im Kommutator)...
$\Delta^{2} x=\langle z|\frac{1}{2}(z^{2}+(z^{\ast})^{2}+z^{\ast}z+1+z^{\ast}z)|z\rangle-\langle z|\frac{1}{\sqrt{2}}(z+z^{\ast}) |z\rangle^{2}$
$\Delta^{2} p=\langle z|-\frac{1}{2}(z^{2}+(z^{\ast})^{2}-z^{\ast}z+1-z^{\ast}z)|z\rangle-\langle z|-\frac{i}{\sqrt{2}}(z-z^{\ast}) |z\rangle^{2}$
vereinfachen...
$\Delta^{2} x=\langle z|\frac{1}{2}(z^{2}+2z^{\ast}z+(z^{\ast})^{2}+1)|z\rangle-\langle z|\frac{1}{\sqrt{2}}(z+z^{\ast}) |z\rangle^{2}$
$\Delta^{2} p=\langle z|-\frac{1}{2}(z^{2}-2z^{\ast}z+(z^{\ast})^{2}+1)|z\rangle-\langle z|-\frac{i}{\sqrt{2}}(z-z^{\ast}) |z\rangle^{2}$
Daraus folgt:
$\Delta^{2} x=\frac{1}{2}$
$\Delta^{2} p=-\frac{1}{2}$
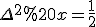
Dann ergäbe
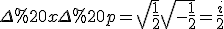
$\Delta x\Delta p=\sqrt{\frac{1}{2}}\sqrt{-\frac{1}{2}}=\frac{i}{2}$
Komplex sollte das wohl nicht sein. - Allerdings habe ich oben in $\Delta^{2} p$ den Kommutator $\left[a^{\dagger},a\right]$ , also die umgekehrte Reihenfolge der Operatoren zu dem wie Du es geschrieben hast. Also, wenn für diesen Kommutator -1 heraus kommt, dann ergäbe auch
$\Delta^{2} p=\frac{1}{2}$
und es wäre
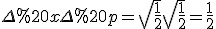
$\Delta x\Delta p=\sqrt{\frac{1}{2}}\sqrt{\frac{1}{2}}=\frac{1}{2}$
Ist wahrscheinlich eher richtig.

So sieht das sehr vernünfitg aus - d.h. kohärente Zustände |z> minimieren für beliebiges z die Heisenbergsche Unschärfenrelation

positronium hat geschrieben: Ist $\left[a,a^{\dagger}\right]$ für jeden Operator mit dem adjungierten Operator immer 1?

Du meinst wahrscheinlich 0?
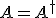
Sollte doch nur der Fall sein, wenn der Operator hermitesch ( $A=A^{\dagger}$ ) oder Unitär( $AA^{\dagger}=A^{\dagger}A=\mathbb{I}$ ) ist?

Schaue 3 Posts weiter oben. Dort rechnet Tom das vor:
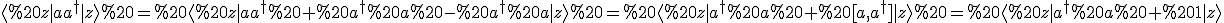
$\langle z|aa^{\dagger}|z\rangle = \langle z|aa^{\dagger} + a^\dagger a - a^\dagger a|z\rangle = \langle z|a^{\dagger} a + [a,a^\dagger]|z\rangle = \langle z|a^{\dagger} a + 1|z\rangle$
Der Kommutator ergibt 1.

Und dass der Kommutator 1 ergbt, folgt speziell aus [x,p] = i.

So, zum Schluss noch die Zeitentwicklung eines kohärenten Zustandes, dann geht's weiter mit dem Skript.

Wir setzen

$H = a^\dagger a + \frac{1}{2} = N + \frac{1}{2}$

und betrachten nur die Zeitentwicklung unter N, da der konstante Term einfach eine triviale Phase ergibt (und nur einem konstanten Term im Potential entspricht).

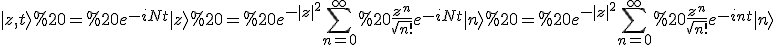
$|z,t\rangle = e^{-iNt}|z\rangle = e^{-|z|^2}\sum_{n=0}^\infty \frac{z^n}{\sqrt{n!}}e^{-iNt}|n\rangle = e^{-|z|^2}\sum_{n=0}^\infty \frac{z^n}{\sqrt{n!}}e^{-int}|n\rangle$

Dabei haben wir N|n> = n|n> verwendet. Nun schreiben wir die e-Funktion um

$|z,t\rangle = e^{-|z|^2}\sum_{n=0}^\infty \frac{\rangle(z\,e^{-it}\rangle^n}{\sqrt{n!}}|n\rangle = e^{-|z(t)|^2}\sum_{n=0}^\infty \frac{z^n(t)}{\sqrt{n!}}|n\rangle$

Dabei gilt

$z(t) = z\,e^{-it}$

$|z(t)| = |z|$

D.h. die Zeitentwicklung eines kohärenten Zustandes entspricht einer Rotation in der komplexen Ebene; insbs. bleibt die Eigenschaft des kohärenten Zustandes erhalten

$z(t) = z\,e^{-it}$

$|z,t\rangle = |z(t)\rangle$

hat hier jemand Erfahung mit Mathematica o.ä.?

tomS hat geschrieben:hat hier jemand Erfahung mit Mathematica o.ä.?

Ja, mit Mathematica. Es ist aber nicht so, dass ich mich in jedem Eckchen dieses gigantischen Werkzeugs auskenne.

Frage: kannst du mal die Ortsdarstellung der kohärenten Zustände in Mathematica berechnen bzw. darstellen?

Ansatz wie folgt:

http://en.wikipedia.org/wiki/Quantum_ha ... oscillator
http://en.wikipedia.org/wiki/Coherent_states

$u_n(x) = e^{-x^2/2}H_n(x)$

wobei H[down]n[/down](x) den Hermitefunktionen entspricht.

Dann berechnet man

$\psi_z(x) = \langle x|z\rangle = \sum_{n=0}^\infty\langle x|n\rangle\langle x|z\rangle = e^{-|z|^2/2} \sum_{n=0}^\infty u_n(x) \frac{z^n}{\sqrt{n!}} = e^{-|z|^2/2} e^{-x^2/2}\sum_{n=0}^\infty \frac{z^n}{\sqrt{n!}} H_n(x)$

Kannst Du mir noch etwas über die Variablen sagen - ich brauche noch etwas, damit die Vereinfachung klappt, also Wertebereiche, zugrunde liegende Zahlenmengen etc..
Jetzt hat Mathematica ein Problem mit sqrt[n!] und kann deshalb die Summe nicht heraus rechnen. Wenn ich die Wurzel weg lasse, klappts. Oder wie kann ich das umschreiben?

Abenteuer-Universum

Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen

Re: Einführung in die Quantenmechanik - Übungen